
家庭拿四 2 二次函数的图象与性质 第2课时 二次函数y=ax2+k的图象与性质
2 二次函数的图象与性质 第2课时 二次函数y=ax2+k的图象与性质

基础自主梳理 导 核心心重难探究 航 新知训川练巩固 素能演练提升
导 航 基础自主梳理 核心重难探究 新知训练巩固 素能演练提升

基础自主梳理 1.二次函数y=2x2,y=2x2+1y=2x2-1的图象都是抛物线,并且 形状相同,只是位置不同.将函数y=2x2的图象向上平 移1个单位长度,就得到函数y=2x2+1的图象;将函数y=2x2的 图象向下平移1个单位长度,就得到函数y=2x21的图象. 温馨提示 1.一般地,二次函数y=x2+k的图象是抛物线,它与抛物线 y=心2的形状、开口方向和开口大小相同,只是在坐标系中的 位置不同.将地物线y=2向上或向下平移k个单位长度便得 到抛物线y=2+k.当k>0时,向上平移;当k<0时,向下平移, 导航页
导航页 基础自主梳理 1.二次函数y=2x 2 ,y=2x 2+1,y=2x 2 -1的图象都是抛物线,并且 形状 ,只是 不同.将函数y=2x 2的图象向上平 移1个单位长度,就得到函数 的图象;将函数y=2x 2的 图象向下平移1个单位长度,就得到函数 的图象. 温馨提示 1.一般地,二次函数y=ax2+k的图象是抛物线,它与抛物线 y=ax2的形状、开口方向和开口大小相同,只是在坐标系中的 位置不同.将抛物线y=ax2向上或向下平移|k|个单位长度便得 到抛物线y=ax2+k.当k>0时,向上平移;当k<0时,向下平移. 相同 位置 y=2x 2+1 y=2x 2 -1
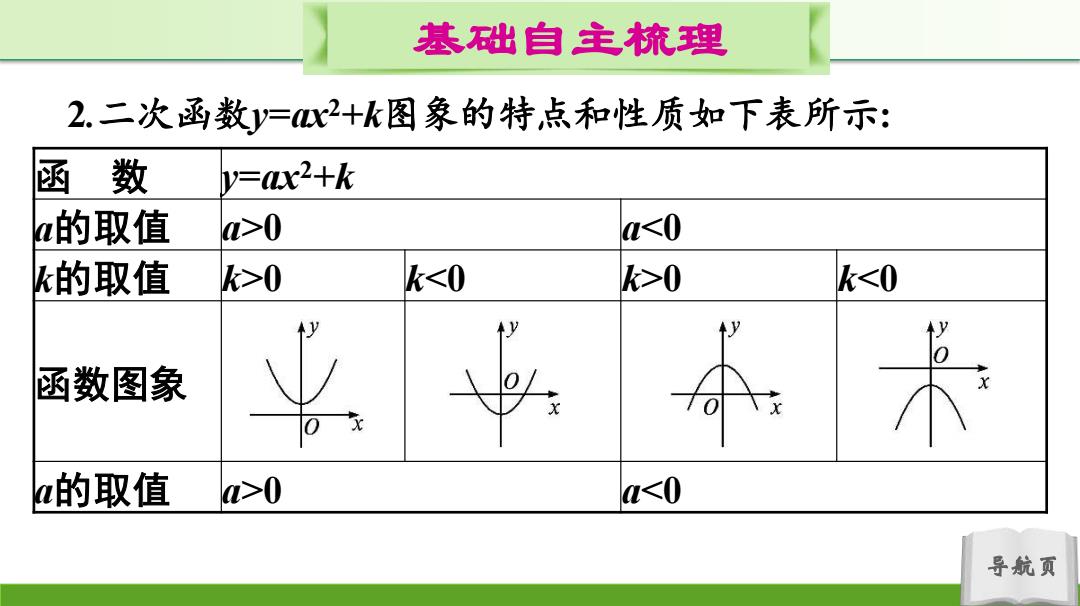
基础自主梳理 2.二次函数y=x2+k图象的特点和性质如下表所示: 函数 y=ax2+k a的取值 >0 a<0 k的取值 k>0 k<0 k>0 k<0 y 函数图象 a的取值 a>0 a<0 导航页
导航页 基础自主梳理 2.二次函数y=ax2+k图象的特点和性质如下表所示: 函 数 y=ax2+k a的取值 a>0 a<0 k的取值 k>0 k<0 k>0 k<0 函数图象 a的取值 a>0 a<0

基础自主梳理 开口方向 向上 向下 对称轴 y轴 顶点坐标 (0,k) 当x=0时,函数有最 函数最值 当x=0时,函数有最大值为k 小值为k 当x<0时y随x的增 当x<h时y随x的增大而增 大而减小; 函数增减性 大 当x>0时y随x的增 当x>h时,y随x的增大而减 大而增大 小 导航页
导航页 基础自主梳理 开口方向 向上 向下 对称轴 y轴 顶点坐标 (0,k) 函数最值 当x=0时,函数有最 小值为k 当x=0时,函数有最大值为k 函数增减性 当x<0时,y随x的增 大而减小; 当x>0时,y随x的增 大而增大 当x<h时,y随x的增大而增 大; 当x>h时,y随x的增大而减 小