
家庭们亚 5】 三角函数的应用 第1课时 方向角
5 三角函数的应用 第1课时 方向角

基础自主梳理 导 核心心重难探究 航 新知训川练巩固 素能演练提升
导 航 基础自主梳理 核心重难探究 新知训练巩固 素能演练提升
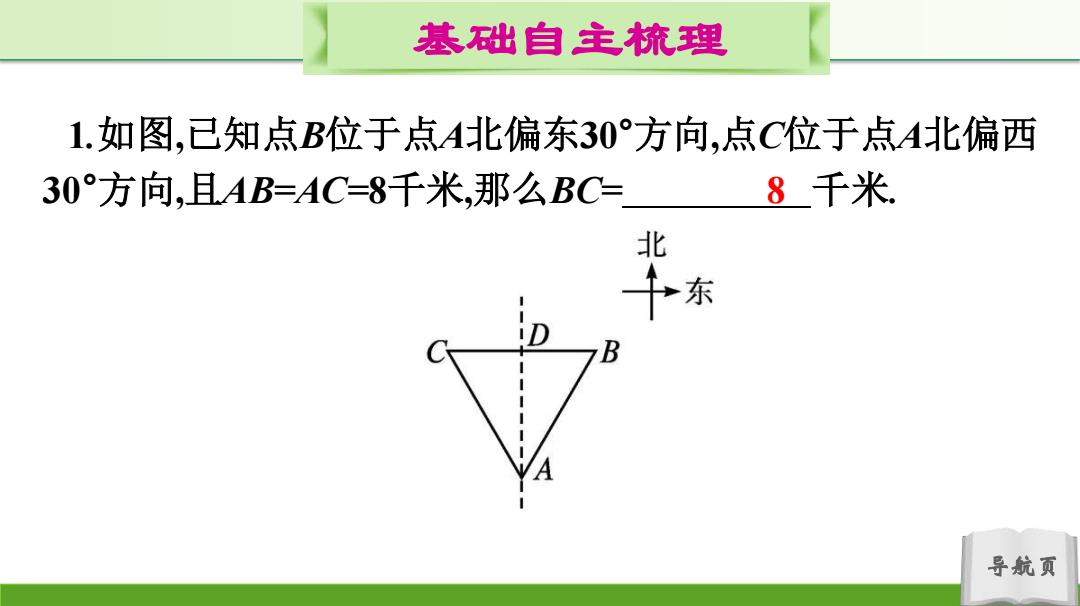
基础自主梳理 1.如图,已知点B位于点A北偏东30°方向,点C位于点A北偏西 30°方向,且AB=AC=8千米,那么BC= 8千米 北 东 导航页
导航页 基础自主梳理 1.如图,已知点B位于点A北偏东30°方向,点C位于点A北偏西 30°方向,且AB=AC=8千米,那么BC= 8 千米

基础自主梳理 2.如图,小明从A处出发,要到北偏东60°方向的C处,他先沿正 东方向走了200米到达B处,再沿北偏东30°方向走恰好能到达 目的地C处则B,C两地的距离为 200米 牛东 60° 396 导航页
导航页 基础自主梳理 2.如图,小明从A处出发,要到北偏东60°方向的C处,他先沿正 东方向走了200米到达B处,再沿北偏东30°方向走恰好能到达 目的地C处.则B,C两地的距离为 200米

核心重难探究 知识点一:求路程问题 【例1】如图,一艘海监船在某岛附近海域 北 巡航,某一时刻海监船在A处测得该岛上某一 东 目标C在它的北偏东45°方向,海监船沿北偏 西30°方向航行60海里后到达B处,此时测得 北 该目标C在它的南偏东75°方向,求此时该船 东 与目标C之间的距离CB的长度.(结果保留根号) 思路点拨:(1)利用BC所在的△ABC能否直接求出BC的长? (2)怎样构造直角三角形求解? 导航页
导航页 核心重难探究 知识点一:求路程问题 【例1】如图,一艘海监船在某岛附近海域 巡航,某一时刻海监船在A处测得该岛上某一 目标C在它的北偏东45°方向,海监船沿北偏 西30°方向航行60海里后到达B处,此时测得 该目标C在它的南偏东75°方向,求此时该船 与目标C之间的距离CB的长度.(结果保留根号) 思路点拨:(1)利用BC所在的△ABC能否直接求出BC的长? (2)怎样构造直角三角形求解?