
家庭缠四 5 二次函数与一元二次方程 第1课时 二次函数与一元二次方程的关系
5 二次函数与一元二次方程 第1课时 二次函数与一元二次方程的关系

基础自主梳理 导 核心心重难探究 航 新知训川练巩固 素能演练提升
导 航 基础自主梳理 核心重难探究 新知训练巩固 素能演练提升

基础自主梳理 1.二次函数y=x2+bx+c的图象与x轴的交点有三种情 况:有两个交点、有一个交点、没有交点 与此相对应,一元二次方程x2+bx+c=0的根也有三种情况: 有两个不相等的实数根、有两个相等的实数根、没有实数根 2.二次函数y=x2+bx+c的图象与x轴交点的横坐标就是 一元二次方程x2+bx+c=0的根 导航页
导航页 基础自主梳理 1.二次函数y=ax2+bx+c的图象与x轴的交点有三种情 况: . 与此相对应,一元二次方程ax2+bx+c=0的根也有三种情况: . 2.二次函数y=ax2+bx+c的图象与x轴交点的 就是 一元二次方程ax2+bx+c=0的根. 有两个交点、有一个交点、没有交点 有两个不相等的实数根、有两个相等的实数根、没有实数根 横坐标
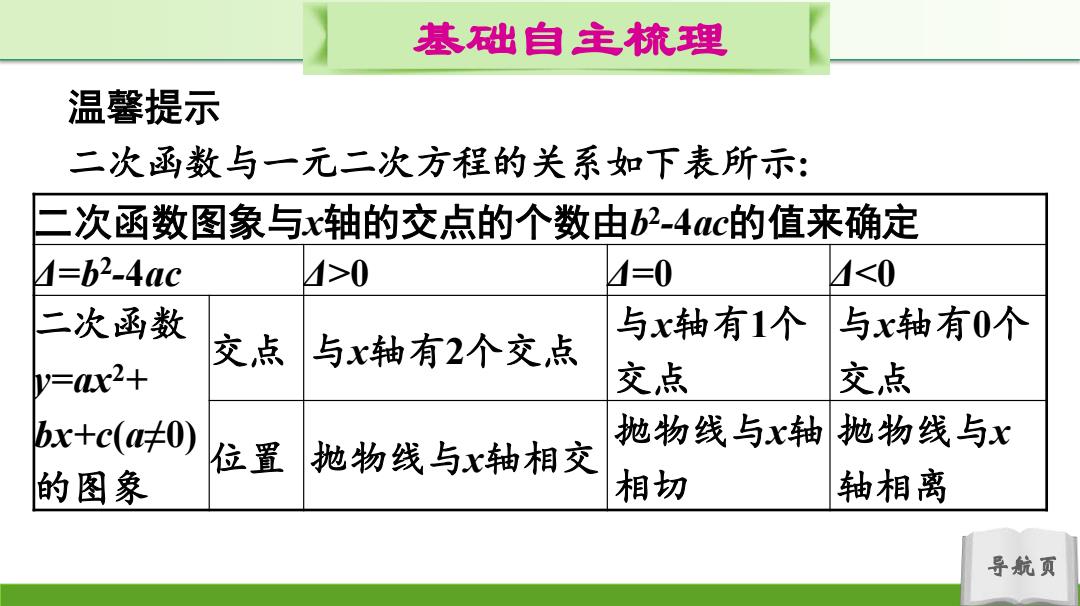
基础自主梳理 温馨提示 二次函数与一元二次方程的关系如下表所示: 二次函数图象与x轴的交点的个数由b2-4c的值来确定 1=b2-4ac >0 =0 M<0 二次函数 与x轴有1个 与x轴有0个 交点与x轴有2个交点 y=x2+ 交点 交点 bx+c(呋0) 抛物线与轴 地物线与X 位置抛物线与x轴相交 的图象 相切 轴相离 导航页
导航页 基础自主梳理 温馨提示 二次函数与一元二次方程的关系如下表所示: 二次函数图象与x轴的交点的个数由b 2 -4ac的值来确定 Δ=b2 -4ac Δ>0 Δ=0 Δ<0 二次函数 y=ax2+ bx+c(a≠0) 的图象 交点 与x轴有2个交点 与x轴有1个 交点 与x轴有0个 交点 位置 抛物线与x轴相交 抛物线与x轴 相切 抛物线与x 轴相离
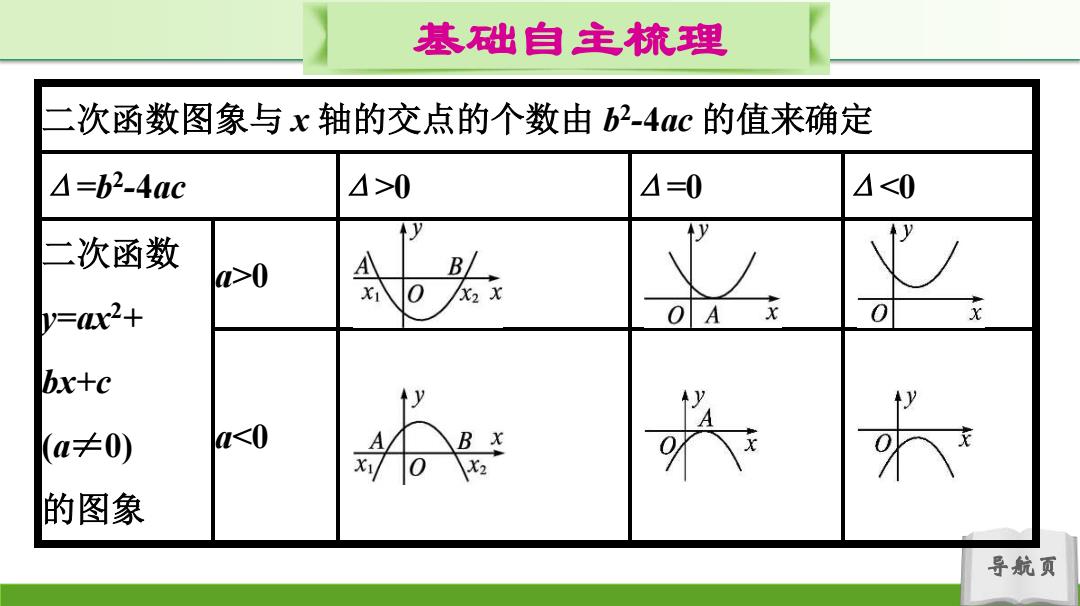
基础自主梳理 次函数图象与x轴的交点的个数由b24c的值来确定 △=b2.4ac 4>0 么=0 <0 y 二次函数 >0 B =x2+ 0 X bx+C ↑y (a≠0) a<0 B¥ 0 2 的图象 导航页
导航页 基础自主梳理 二次函数图象与 x 轴的交点的个数由 b 2 -4ac 的值来确定 Δ=b2 -4ac Δ>0 Δ=0 Δ<0 二次函数 y=ax2 + bx+c (a≠0) 的图象 a>0 a<0