
附 二项分布 1.二项分布的定义 如果一种过程(随机实验)的结局只能是相 互对立的两种结果中的一种,例如射击的命中与 未中、治疗的有效与无效、实验动物染毒后的生 存与死亡等等,其中一种结果发生的可能性(概 率)为一常数π,被观察的n个观察单位的结局之 间相互独立,记录个观察单位中发生某一种结 果的频数X,则称随机变量X服从二项分布 吉林大学远程教育学院
2 吉林大学远程教育学院 附 二项分布 1.二项分布的定义 如果一种过程(随机实验)的结局只能是相 互对立的两种结果中的一种,例如射击的命中与 未中、治疗的有效与无效、实验动物染毒后的生 存与死亡等等,其中一种结果发生的可能性(概 率)为一常数π,被观察的n个观察单位的结局之 间相互独立,记录n个观察单位中发生某一种结 果的频数X,则称随机变量X 服从二项分布

(Binomial distribution)。常记x~B(n,π)。二 项分布属于离散型分布。 2.二项分布的概率 p(X)=CX(1-πy”Xπ' X=0,1,2,,n 其中 C= XI(n-X! 3.二项分布的图形 在应用中,常通过形如下图的图形表达(或描 述)二项分布变量的分布状况。 吉林大学远程教育学院
3 吉林大学远程教育学院 (Binomial distribution)。常记X ~ B(n,π)。二 项分布属于离散型分布。 2.二项分布的概率 ( ) X n X X p X Cn − ( ) = 1− X = 0,1,2,..., n 其中 !( )! ! X n X n C X n − = 3.二项分布的图形 在应用中,常通过形如下图的图形表达(或描 述)二项分布变量的分布状况
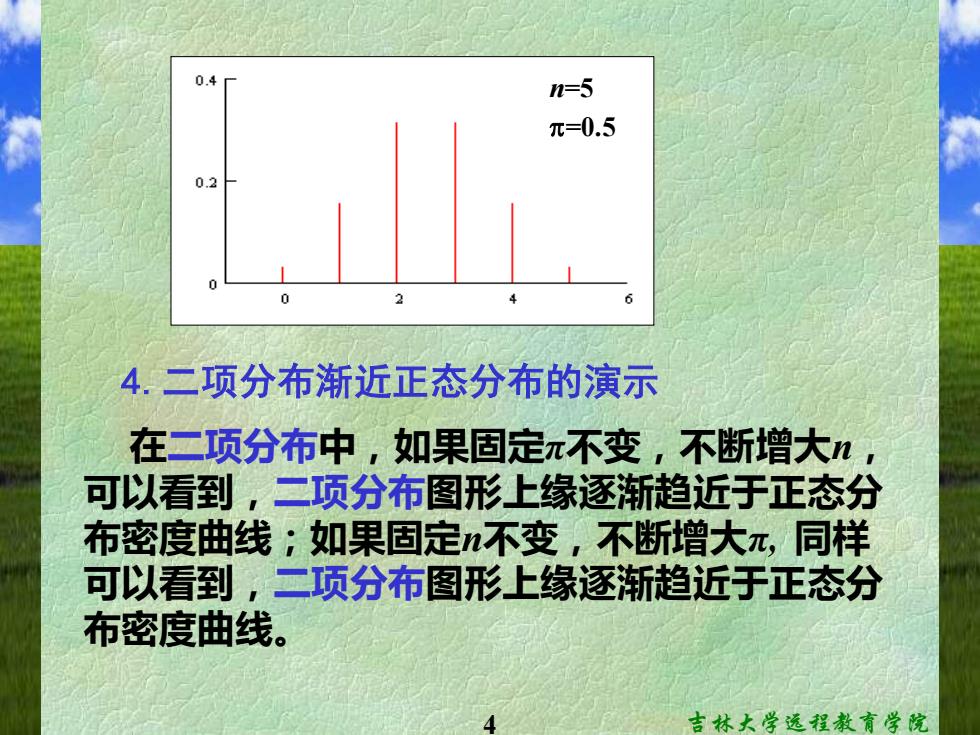
0.4 n=5 元=0.5 02 4.二项分布渐近正态分布的演示 在二项分布中,如果固定π不变,不断增大n, 可以看到,二项分布图形上缘逐渐趋近于正态分 布密度曲线;如果固定不变,不断增大π,同样 可以看到,二项分布图形上缘逐渐趋近于正态分 布密度曲线。 吉林大学远程散育学院
4 吉林大学远程教育学院 n=5 =0.5 4.二项分布渐近正态分布的演示 在二项分布中,如果固定π不变,不断增大n, 可以看到,二项分布图形上缘逐渐趋近于正态分 布密度曲线;如果固定n不变,不断增大π, 同样 可以看到,二项分布图形上缘逐渐趋近于正态分 布密度曲线
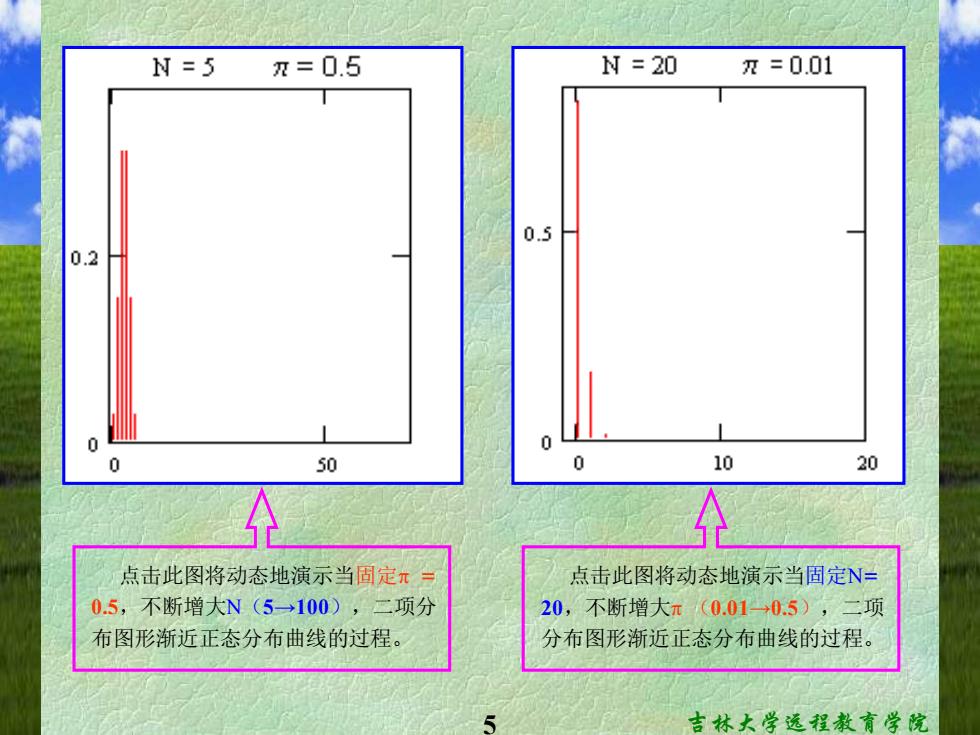
N=5 π=0.5 N=20 π=0.01 0.5 0.2 0 50 10 20 点击此图将动态地演示当固定π 点击此图将动态地演示当固定N 0.5,不断增大N(5→100),二项分 20,不断增大π(0.01→0.5),二项 布图形渐近正态分布曲线的过程。 分布图形渐近正态分布曲线的过程。 吉林大学远程教育学院
5 吉林大学远程教育学院 点击此图将动态地演示当固定 = 0.5,不断增大N(5→100),二项分 布图形渐近正态分布曲线的过程。 点击此图将动态地演示当固定N= 20,不断增大 (0.01→0.5),二项 分布图形渐近正态分布曲线的过程

5.二项分布的正态近似条件 在应用中,当π或1-π不太小,而足够大,如 p和(p≥5,我们常用正态近似原理来处理二项 分布的问题,此为二项分布的正态近似条住。在实 际中,可用p估计π。 6.二项分布的均数与标准差 均数 l=nπ 标准差 o=/nπ(1-π) 吉林大学远程教育学院
6 吉林大学远程教育学院 5.二项分布的正态近似条件 在应用中,当π或1-π不太小,而n足够大,如 np和n(1-p)≥5,我们常用正态近似原理来处理二项 分布的问题,此为二项分布的正态近似条件。在实 际中,可用p 估计π。 6.二项分布的均数与标准差 均数 标准差 = n = n(1−)