
第八节 方差分析 四、多个样本均数的两两比较的g检验 方差分析后,若推断结论是拒绝H。,则意味着 各组样本均数所代表的总体均数间不同或不全相 同。当要了解任意两总体均数间是否存在差别时, 需在方差分析的基础上进一步做多个样本均数的 两两比较,又称为样本均数间的多重比较。 根据所控制误差的类型和大小不同,均数间 差别的多重比较的方法很多。这里介绍常用的q 检验(Student-Newman-Keuls,SNK)。 吉林大学远程教育学院
2 吉林大学远程教育学院 四、多个样本均数的两两比较的q 检验 方差分析后,若推断结论是拒绝H0,则意味着 各组样本均数所代表的总体均数间不同或不全相 同。当要了解任意两总体均数间是否存在差别时, 需在方差分析的基础上进一步做多个样本均数的 两两比较,又称为样本均数间的多重比较。 根据所控制误差的类型和大小不同,均数间 差别的多重比较的方法很多。这里介绍常用的q 检验(Student-Newman-Keuls, SNK)。 第八节 方差分析

q检验的检验统计量的公式为: 9- 公式(10.30) SxA-Xn 公式(10.31 n nB 式中和,是要比较的两样本均数; 5要,-x。 样本均数之差的标准误;n和ns是要比较的两样本含量; MS误差为方差分析中的误差均方。 吉林大学远程教有学院
3 吉林大学远程教育学院 式中 和 是要比较的两样本均数; 为两 样本均数之差的标准误;nA和nB是要比较的两样本含量; MS误差为方差分析中的误差均方。 q 检验的检验统计量的公式为: X A XB A B S X X q − − = ) 1 1 ( 2 A B X X n n MS S A B = + − 误差 公式(10.30) 公式(10.31) X A XB X A XB S −

q的分布与两比较组之间的组间跨度,及自由度v 有关。组间跨度a是指两对比组间所包含的组数( 包括对比组自身);自由度即为保差。 根据组间跨度a,自由度以及检验水准查q界 值表(见教材后附表5),即qa(v,a)。 当求得q≥qa(v,。)时,按a检验水准拒 绝H。,两对比组间差别有统计学意义;反之,尚 不拒绝H0。 下面对例1022资料作均数间的多重比较。 1 吉林大学远程教育学院
4 吉林大学远程教育学院 q 的分布与两比较组之间的组间跨度a 及自由度ν 有关。组间跨度a 是指两对比组间所包含的组数( 包括对比组自身);自由度ν即为ν误差。 根据组间跨度a ,自由度ν以及检验水准α查 q 界 值表(见教材后附表5),即qα(ν,a) 。 当求得 q ≥ qα(ν,a) 时,按α检验水准拒 绝H0,两对比组间差别有统计学意义;反之,尚 不拒绝H0。 下面对例10.22资料作均数间的多重比较

H0:⅓=B H:WWB 0=0.05 将三个样本均数由大到小排列并编组次: 组次 1 2 3 X 1.62 1.20 0.87 组别 甲法 乙法 丙法 本例n1=n2=n3=6,MS误差=0.03078,代入 吉林大学远程教育学院
5 吉林大学远程教育学院 H0 : μA=μB H1 : μA≠μB α= 0.05 将三个样本均数由大到小排列并编组次: Xi 组次 组别 1.62 1.20 0.87 1 2 3 甲法 乙法 丙法 本例n1= n2= n3=6,MS误差=0.03078,代入
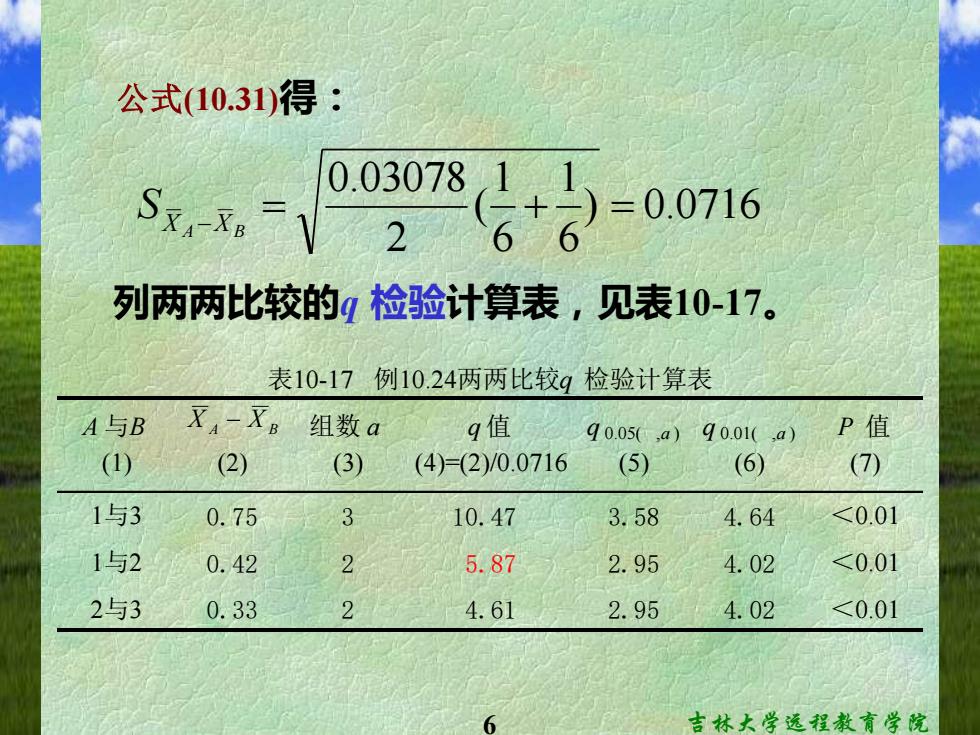
公式(10.31)得: 列两两比较的g检验计算表,见表10-17。 表10-17例10.24两两比较g检验计算表 A与B X4-X。组数a 9值 q0.05,a)90.01(,a) P值 (1) (2) (3) (4)=(2)/0.0716 (5) (6) (7) 1与3 0.75 3 10.47 3.58 4.64 <0.01 1与2 0.42 2 5.87 2.95 4.02 <0.01 2与3 0.33 2 4.61 2.95 4.02 <0.01 吉林大学远程教育学院
6 吉林大学远程教育学院 公式(10.31)得: ) 0.0716 6 1 6 1 ( 2 0.03078 = + = X A −XB S 列两两比较的q 检验计算表,见表10-17。 A 与B 组数 a q 0.05( ,a ) q 0.01( ,a ) P 值 (1) (2) (3) (5) (6) (7) 1与3 0.75 3 10.47 3.58 4.64 <0.01 1与2 0.42 2 5.87 2.95 4.02 <0.01 2与3 0.33 2 4.61 2.95 4.02 <0.01 q 值 (4)=(2)/0.0716 表10-17 例10.24两两比较q 检验计算表 X A − X B