
第十二章非参数统计 第二节 成组设计的两样本比校的 秩和检验 (Wilc0xon两样本比较法) 一、原始数据的两样本比较 例12.2 某实验室观察局部温热治疗小鼠移植肿瘤的疗效,以 生存日数作为观察指标,实验结果见下表12-2。试检验两组小鼠生存 日数有无差别。 吉林大学远程教育学院
2 吉林大学远程教育学院 第十二章 非参数统计 第二节 成组设计的两样本比较的 秩和检验 (Wilcoxon两样本比较法) 一、原始数据的两样本比较 例12.2 某实验室观察局部温热治疗小鼠移植肿瘤的疗效,以 生存日数作为观察指标,实验结果见下表12-2。试检验两组小鼠生存 日数有无差别
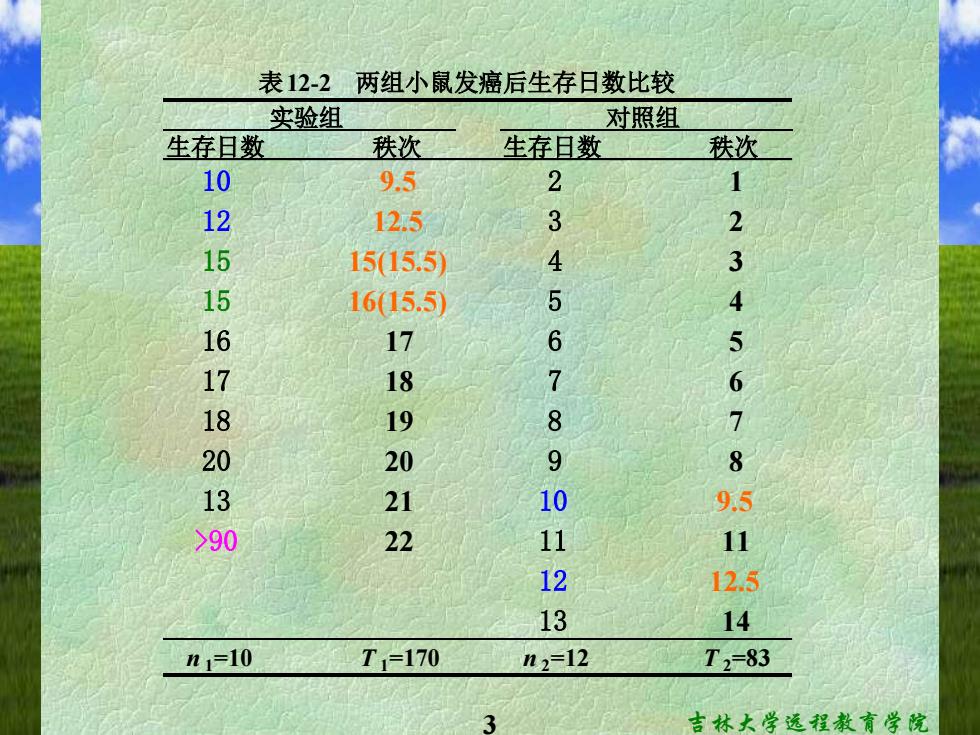
表12-2两组小鼠发癌后生存日数比较 实验组 对照组 生存日数 秩次 生存日数 秩次 10 9.5 2 1 12 12.5 3 2 15 1515.5 4 3 15 16(15.5) 5 4 16 17 6 5 17 18 7 6 18 19 8 7 20 20 9 8 13 21 10 9.5 >90 22 11 11 12 12.5 13 14 n1=10 T=170 n2=12 T2=83 吉林大学远程教育学院
3 吉林大学远程教育学院 实验组 对照组 生存日数 秩次 生存日数 秩次 10 9.5 2 1 12 12.5 3 2 15 15(15.5) 4 3 15 16(15.5) 5 4 16 17 6 5 17 18 7 6 18 19 8 7 20 20 9 8 13 21 10 9.5 >90 22 11 11 12 12.5 13 14 n 1=10 T 1=170 n 2=12 T 2=83 表12-2 两组小鼠发癌后生存日数比较

本例为完全随机设计的两样本比较,由于实验 组的生存日数出现不确定数值(>0),故选用 Wilcoxonj两样本比较法。 本例的检验步骤如下: ①检验假设 H:两组小鼠生存日数总体分布相同 H:两组小鼠生存日数总体分布不同 0a=0.05 ②编秩先将两组数据分别由小到大排庭,再 统一由小到大编秩。相同数值取平均秩次。 见表12-2中的秩次项。 吉林大学远程教育学院
4 吉林大学远程教育学院 本例为完全随机设计的两样本比较,由于实验 组的生存日数出现不确定数值(>90),故选用 Wilcoxon两样本比较法。 H0 : 两组小鼠生存日数总体分布相同 H1 : 两组小鼠生存日数总体分布不同 本例的检验步骤如下: ① 检验假设 α= 0.05 ② 编秩 先将两组数据分别由小到大排序,再 统一由小到大编秩。相同数值取平均秩次。 见表12-2中的秩次项

③求秩和并确定检验统计量分别求每组秩 次和T1与T2。见表12-2中的下列项。 取样本例数较小组的秩和作为检验统计量T,若 例数相等,可任取一组的秩和为T。 本例n1=10较小,则T1=T=170。 ④确定P值和作出推断结论查附表9T界值 表(两样本比较的秩和检验用,n1<n2)儿Tanl,n2-nl), a为检验水准,n1为样本例数较小者,n2-n1 为两组例数差。若检验统计量T值在界值 范围内则P>α:T值在界值范围外,则 P<a:T值等于界值:则P=a。 吉林大学远程教育学院
5 吉林大学远程教育学院 ③ 求秩和并确定检验统计量 分别求每组秩 次和T1与T2。见表12-2中的下列项。 取样本例数较小组的秩和作为检验统计量T,若 例数相等,可任取一组的秩和为T 。 本例n1=10较小,则 T1= T =170。 ④ 确定P值和作出推断结论 查附表9 T界值 表(两样本比较的秩和检验用, n1<n2 )[Tα(n1, n2-n1), α为检验水准,n1为样本例数较小者, n2–n1 为两组例数差]。若检验统计量T值在界值 范围内,则P >α;T值在界值范围外,则 P <α;T值等于界值;则P =α

本例Tal,2n=T0.05102-84-146,而T= 170在界值范围外,故P<0.05,按a= 0.05水准拒绝H。认为实验组生存日数较 对照组长。 二、正态近似法 若n1或n2一n1超出附表9T界值表(两样本比较的秩和 检验里,1<2)的范围,可按下式进行近似的u检验。 T-(n+n2+1)/2-0.5 公式(12.3) √nn2(%,+n2+1)/12 吉林大学远程教育学院
6 吉林大学远程教育学院 二、正态近似法 若n1或n2–n1超出附表9 T界值表(两样本比较的秩和 检验用, n1<n2 )的范围,可按下式进行近似的u 检验。 本例Tα(n1, n2-n1) =T0.05(10,2)=84-146,而T= 170在界值范围外,故P < 0.05,按α= 0.05水准拒绝H0。认为实验组生存日数较 对照组长。 ( 1)/12 ( 1)/ 2 0.5 1 2 1 2 1 1 1 2 + + − + + − = n n n n T n n n u 公式(12.3)