
应用换元公式时应注意:(1)用x =β(t)把变量x 换成新变量 时,积分限也相应的改变(2)求出,f[(t)l'(t)的一个原函数Φ(t)后,不必象计算不定积分那样再要把Φ(t)变换成原变量x的函数,而只要把新变量 的上、下限分别代入Φ(t)然后相减就行了配元不换限(3)换元公式也可反过来使用,即β [p(t)lp'(t) dt= ~f(x)dx(令 x = (t))7或配元f[p(t)]p'(t) dt = [~ f[ p(t)1 d p(t)
应用换元公式时应注意: (1) 求出 f [(t)](t)的一个原函数(t)后,不 必象计算不定积分那样再要把(t)变换成原 变量x 的函数,而只要把新变量t 的上、下限 分别代入(t)然后相减就行了. (2) 用x = (t)把变量x 换成新变量t 时,积分限也 相应的改变. (3) 换元公式也可反过来使用 , 即 f x x (令 x = (t)) b a ( )d = 或配元 (t) d(t) (t) (t) (t) (t) 配元不换限
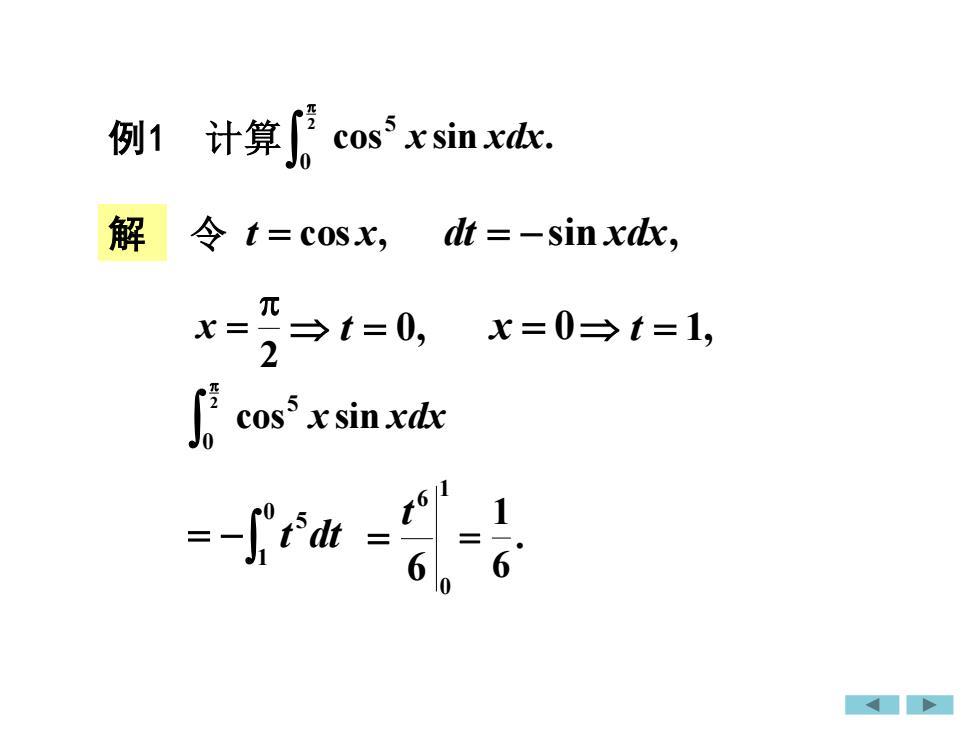
2-计算例1cos' x sin xdx.0解令 t=cosx,dt = -sin xdx,元t= 0,x=0=t=1x225cos' x sin xdx10D1
例1 计算 cos sin . 2 0 5 x xdx 解 令 t = cos x, 2 x = t = 0, x = 0 t = 1, 2 0 5 cos x sin xdx = − 0 1 5 t dt 1 0 6 6 t = . 6 1 = dt = −sin xdx
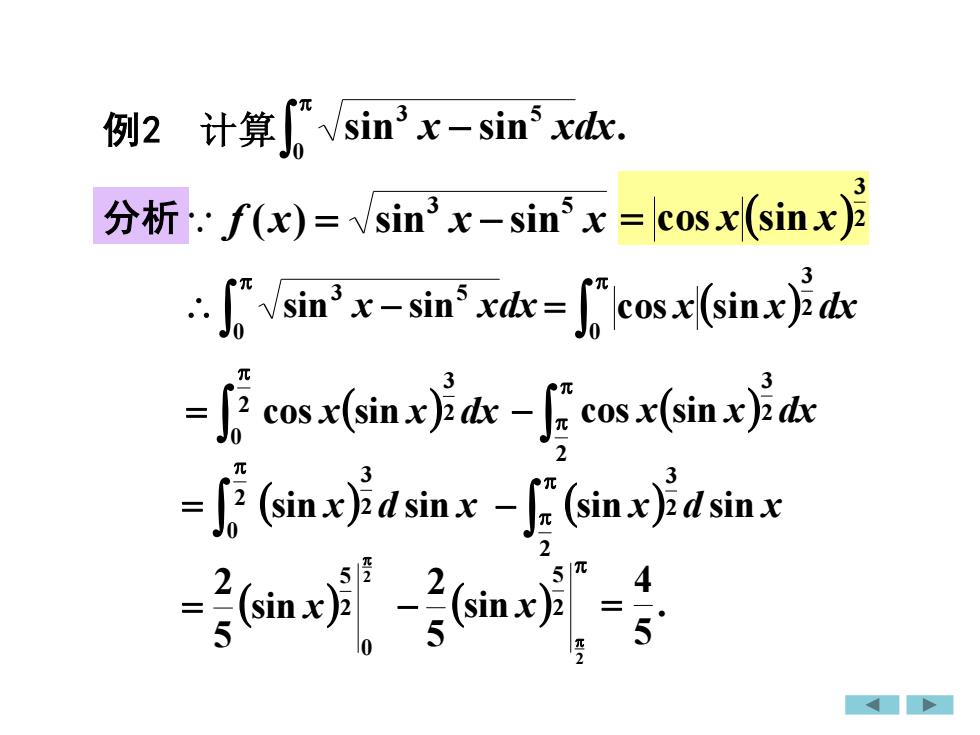
"sin'x - sinxdx.例2计算分析:f(x)=/sin'x-sin'x=|cosx(sinx)"cos x(sinx)2dxVsin x - sin xdx =Je cos x(sin x) dx - f cos x(sin x) dx102元32(sinx)d sinx -1[" (sin x)2d sin x-J022242sinxsin5720
例2 计算 分析 sin sin . 0 3 5 x − xdx f x x x 3 5 ( ) = sin − sin ( )2 3 = cos x sin x − 0 3 5 sin x sin xdx ( ) = 0 2 3 cos x sin x dx ( ) = 2 0 2 3 cos x sin x dx ( ) − 2 2 3 cos x sin x dx ( ) = 2 0 2 3 sin x d sin x ( ) − 2 2 3 sin x d sin x ( ) 2 0 2 5 sin 5 2 = x ( ) − 2 2 5 sin 5 2 x . 5 4 =

3dxe4例3计算x/In x(1 - In x)3d(lnx)04分析原式=fe/Inx(1 - Inx)33d(lnx)d/InxIn x(1- lnx)1-(/lnx)3T 2arcsin(/In x)6
例3 计算 分析 . ln (1 ln ) 4 3 − e e x x x dx 原式 − = 4 3 ln (1 ln ) e (ln ) e x x d x − = 4 3 ln (1 ln ) e (ln ) e x x d x − = 4 3 2 1 ( ln ) ln 2 e e x d x 4 3 2 arcsin( ln ) e e = x . 6 =

1adx.(a>0)例4计算x+a?x解dx = acos tdt,令x=asint,元x=0=t=0.tx=a=2元acost2原式 =dt1asint+ a?(1-sin't)元costcost - sint22dt1+dt2 JoJ0sint +costsint + cos t元元元[nsin t+ cos = ".2 22
例4 计算 解 + − a dx a x a x 0 2 2 . ( 0) 1 令 x = asint, x = a , 2 t = x = 0 t = 0, dx = acostdt, 原式 + − = 2 0 2 2 sin (1 sin ) cos dt a t a t a t + = 2 0 sin cos cos dt t t t + − = + 2 0 sin cos cos sin 1 2 1 dt t t t t 2 0 lnsin cos 2 1 2 2 1 + + = t t . 4 =