
二、矩阵的初等变换1.定义,下面三种变换称为矩阵的初等行变换(1)对调两行(对调i,j两行,记作r《r);(2)以数k10乘以某一行的所有元素;(第i行乘k,记作rk)(3)把某一行所有元素的k倍加到另一行对应的元素上去(第i行的k倍加到第i行上记作r+kr)
1.定义 下面三种变换称为矩阵的初等行变换: 二、矩阵的初等变换

2.同样可定义矩阵的初等列变换(所用记号是把r换成“c"),包括如下的三种变换。(1)对调矩阵中的两列。(2)以非零常数k乘以矩阵某一列的全部元素。(3)把矩阵中某一列全部元素的k倍加到另外一列的对应元素上。3.矩阵的初等行变换与初等列变换统称为初等变换r《 rj,kr,kr,+rj简记为:行变换列变换C,《 Cj,kc,,kc,+cj
3. 矩阵的初等行变换与初等列变换统称为初等变换. 2. 同样可定义矩阵的初等列变换(所用记号是把“r” 换成“c”),包括如下的三种变换。 简记为:行变换 列变换

引例今有鸡免同笼,上有三十五头,下有九十四足,向鸡免各几何?设鸡有x1只,兔子有x2只350al1i x+x =35六2 494↑ 2x +4x, = 94
引例 今有鸡兔同笼,上有三十五头,下有九十四足,问鸡 兔各几何?
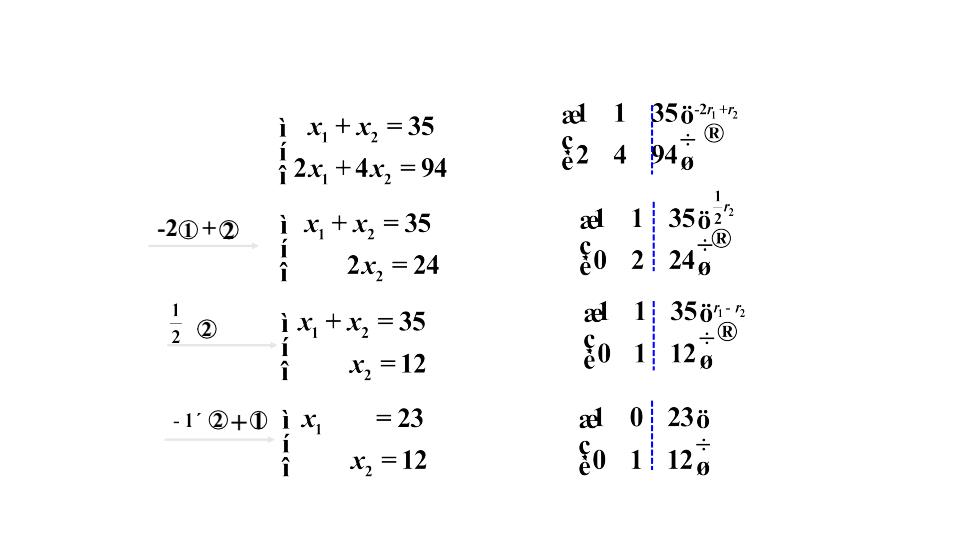
1aelβ5o-2ri +r2i x +x, =35?p4&24i2x, +4x, = 941350231ali x, +x, = 35-2+@?So22402x, =24al11i3501-2 +x, = 35ix,?2BSo11 =12<0:230adl= 23-1'@+@ i x1<1112So11x, =12
-2 1 + 2 2 2 + 1

i3x, - x, +5x, =3ii上例1采用矩阵行初等变化来求解:X - X +2x =1kxi-2x,-X, =21520- 2-12 8.22 °-1302-1do--1BoBor-ael:80.0.-+1232-12131-11:-1- 1+-5r+rco1-r《rel3r+r3-0+36&0S13382-155800- 2-1- 72-012:O·eoc10 α10i8o-2000:X:0718o2-7271-1一C3r.rncoii1+114-0CO11131+ro10-2r,t7-C307-r3+r7-X2iO272中001902+1070.012i·7070X3ii7
上例1 采用矩阵行初等变化来求解: