
2.区域 (1)内点、外点、边界点 设有点集E及一点P: 若存在点P的某邻域U(P)cE, 则称P为E的内点; 若存在点P的某邻域U(P)nE=② 则称P为E的外点, ·若对点P的任一邻域UP)内既含有属于的点也含有 不属于E的点则称P为E的边界点. 显然E的内点必属于E,E的外点必不属于E,E的 边界点可能属于E,也可能不属于E
2. 区域 (1) 内点、外点、边界点 设有点集 E 及一点 P : • 若存在点 P 的某邻域 U(P) E , • 若存在点 P 的某邻域 U(P)∩ E = , • 若对点 P 的任一邻域 U(P) 内既含有 属于E的点也含有 不属于E E 则称 P 为 E 的内点; 则称 P 为 E 的外点 ; 则称 P 为 E 的边界点 . 机动 目录 上页 下页 返回 结束 的点 , 显然, E 的内点必属于 E , E 的外点必不属于 E , E 的 边界点可能属于 E, 也可能不属于 E

(2)聚点 若对任意给定的δ,点P的去心 邻域U(P,δ)内总有E中的点,则 称P是E的聚点 聚点可以属于E,也可以不属于E(因为聚点可以为 E的边界点) 所有聚点所成的点集称为E的导集 目录 上页下页返回结束
(2) 聚点 若对任意给定的 , 点P 的去心 机动 目录 上页 下页 返回 结束 E 邻域 内总有E 中的点 , 则 称 P 是 E 的聚点. 聚点可以属于 E , 也可以不属于 E (因为聚点可以为 所有聚点所成的点集称为 E 的导集 . E 的边界点 )

(3)开区域及闭区域 ·若点集E的点都是内点,则称E为开集; ·E的边界点的全体称为E的边界,记作E, ·若点集EoE,则称E为闭集; ·若集D中任意两点都可用一完全属于D的折线相连 则称D是连通的; ●连通的开集称为开区域,简称区域; ·开区域连同它的边界一起称为闭区域
D (3) 开区域及闭区域 • 若点集 E 的点都是内点,则称 E 为开集; • 若点集 E E , 则称 E 为闭集; • 若集 D 中任意两点都可用一完全属于 D 的折线相连 , • 开区域连同它的边界一起称为闭区域. 则称 D 是连通的 ; • 连通的开集称为开区域 ,简称区域 ; 机动 目录 上页 下页 返回 结束 。 。 • E 的边界点的全体称为 E 的边界, 记作E ;
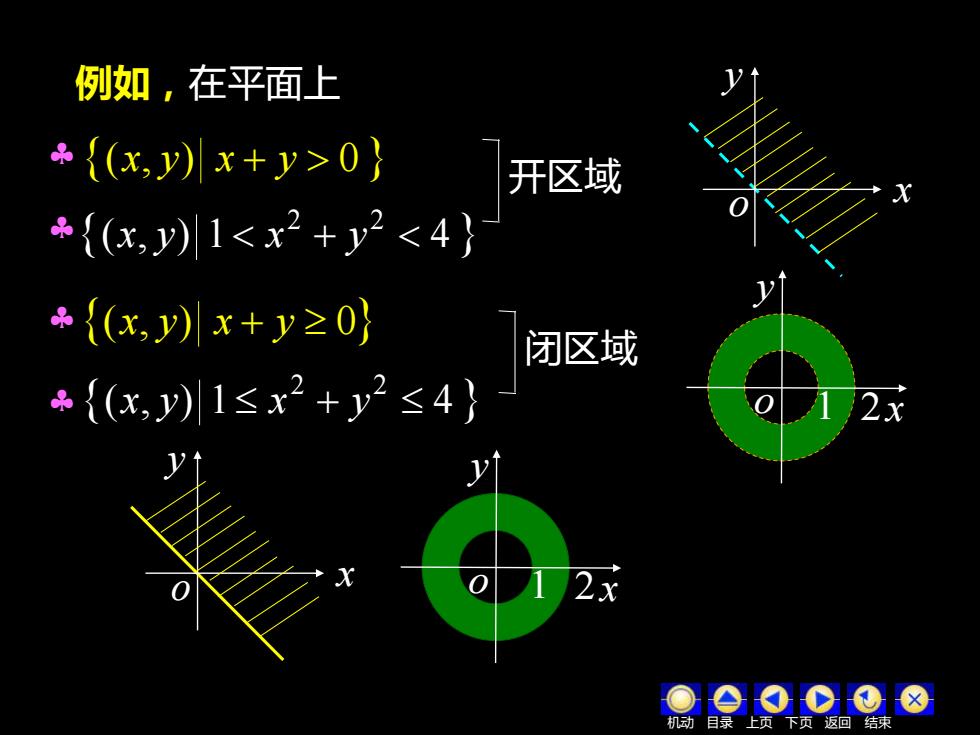
例如,在平面上 {(x,y川x+y>0} 开区域 *{(x,y川1<x2+y2<4} {(x,)x+y≥0} 闭区域 {(x,y)1≤x2+y2≤4) 上页下页返回结束
例如,在平面上 (x, y) x + y 0 ( , ) 1 4 2 2 x y x + y (x, y) x + y 0 ( , ) 1 4 2 2 x y x + y 开区域 闭区域 机动 目录 上页 下页 返回 结束x y o 1 2 x y o x y o x y o 1 2

整个平面是最大的开域 也是最大的闭域; 点集{(x,y)x>}是开集 但非区域. 对点集E,若存在正数r,使得EcU(O,r), 则称E为有界集,否则称为无界集 结
整个平面 点集 (x, y) x 1 是开集, 是最大的开域 , 也是最大的闭域; 但非区域 . 机动 目录 上页 下页 返回 结束 −1 o 1 x y • 对点集 E , 若存在正数 r , 使得 E U O r ( , ), 则称 E 为有界集 , 否则称为无界集