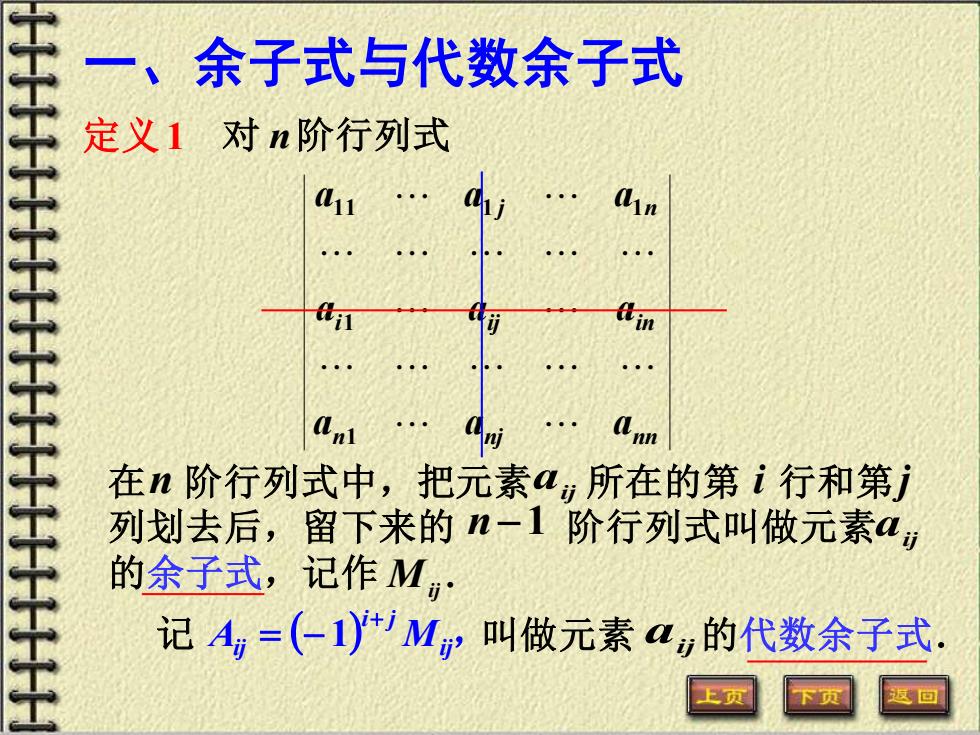
一、余子式与代数余子式 定义1对n阶行列式 在n阶行列式中,把元素a,所在的第i行和第i 列划去后,留下来的n-1阶行列式叫做元素a 的余子式,记作M, 记A,=(-1)'M叫做元素4,的代数余子式
一、余子式与代数余子式 定义1 对 n阶行列式 n nj nn i ij in j n a a a a a a a a a 1 1 11 1 1 在 阶行列式中,把元素 所在的第 行和第 列划去后,留下来的 阶行列式叫做元素 的余子式,记作 n aij i j n −1 aij M . ij ( ) ij, i j Aij M + 记 = − 1 叫做元素 aij 的代数余子式.

例如对 11 12 13 L14 11 l12 L14 023 D= 2…22 M23= a31 432 l34 31 32 34 L41 L42 L44 41 L42 L43 L44 423=(1)2+3M23=-M23,叫做元素a2的代数余子式 注意:一个元素的代数余子式识与该元素所处位置 相关;而与该元素等于多少无关! 比如上例中,即便把2的值换成a3,它的 代数余子式仍然不变!亦即仍有A3=-M3
例如对 , 41 42 43 44 31 32 33 34 21 22 23 24 11 12 13 14 a a a a a a a a a a a a a a a a D = 41 42 44 31 32 34 11 12 14 23 a a a a a a a a a M = ( ) 23 2 3 A23 1 M + = − , = −M23 . 叫做元素a23的代数余子式 注意:一个元素的代数余子式只与该元素所处位置 相关;而与该元素等于多少无关! 代数余子式仍然不变!亦即仍有 比如上例中,即便把 a2 3的值换成 a3 3,它的 A23 = −M23

按照这个定义,对三阶行列式,有 1141213 212223 41122033+凸12423431+0132132 1432 q433 -011423432-412421433-13022431 =41(42243-423432)+412(a23431-021433) +013(421432-22031) 2 =11M11-412M12+413M13 =011A1+12A12+a13A13 上式推广后即得 上页
1 1 2 3 3 2 1 2 2 1 3 3 1 3 2 2 3 1, 1 1 2 2 3 3 1 2 2 3 3 1 1 3 2 1 3 2 a a a a a a a a a a a a a a a a a a − − − = + + 31 32 33 21 22 23 11 12 13 a a a a a a a a a ( ) = a11 a22a33 − a23a32 ( ) + a12 a23a31 − a21a33 ( ) + a13 a21a32 − a22a31 31 32 21 22 13 31 33 21 23 12 32 33 22 23 11 a a a a a a a a a a a a a a = a − + 按照这个定义,对三阶行列式,有 = a11M11 − a12M12 + a13M13 = a11A11 + a12A12 + a13A13 上式推广后即得

二、行列式按行(列)展开法则 定理1n阶行列式等于它的任一行(列)的各 元素与其对应的代数余子式乘积之和,即 L11 12 D 21 l22 a2n : Anl an2 =a1h+024++a4n=a4 (i=1,2,,n) 回
定理1 n 阶行列式等于它的任一行(列)的各 元素与其对应的代数余子式乘积之和,即 = = + + + = n k ai Ai ai Ai ainAin aik Aik 1 1 1 2 2 (i = 1,2, ,n) 二、行列式按行(列)展开法则 n n nn n n a a a a a a a a a D 1 2 21 22 2 11 12 1 =

事实上,n阶行列式也可以按第i列展开: 011 12 (yn D= 21 22 。 。。 Anl Un2 =a4+,4++an4与=0y4g j=1,2,,n) 上页
事实上,n阶行列式也可以按第j 列展开: ( j = 1,2, ,n) n n nn n n a a a a a a a a a D 1 2 21 22 2 11 12 1 = = = + + + = n k a jA j a jA j anjAnj ak jAk j 1 1 1 2 2