《高等数学》课程教学资源（PPT课件）Ⅱ_D11_7斯托克斯公式

为便于记忆，斯托克斯公式还可写作 dydz dzdx dxdy a 8x 0y Dz =$Pdx+Qdy+Rd= P R 或用第一 类曲面积分表示 cos a cos B cosλ a ds=手Pdx+dy+RdE Q 定理1目录上页下页返回结束

为便于记忆, 斯托克斯公式还可写作:         P Q R x y z d y d z d z d x d x d y  = Pd x + Qd y + Rd z 或用第一类曲面积分表示: S P Q R x y z d cos cos cos             = Pd x + Qd y + Rd z 定理1 目录 上页 下页 返回 结束

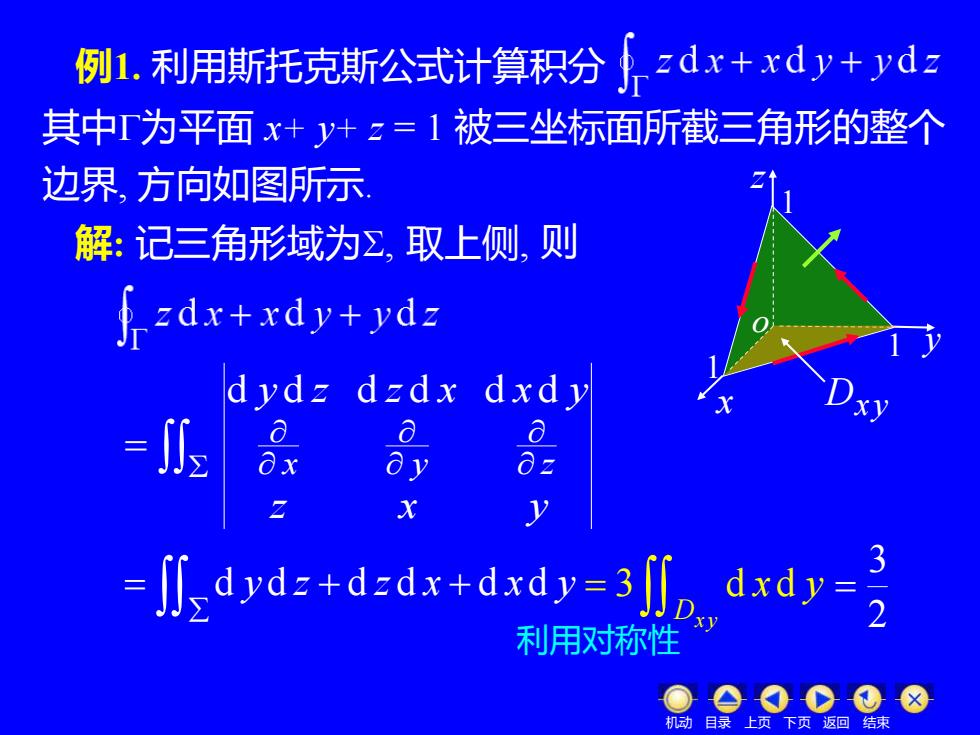
例1.利用斯托克斯公式计算积分dx+xdy+ydz 其中T为平面x+y+z=1被三坐标面所截三角形的整个 边界，方向如图所示 解：记三角形域为Σ，取上侧，则 }=dx+xdy+ydz dydz dzdx dxdy -f 品 y -fdvd=+d-dx+dxdv-3dxdy- 利用对称性 机动目 下页返回结束

z x y y z z x x y x y  z       = d d d d d d z x y 1 1 1 o 例1. 利用斯托克斯公式计算积分 其中为平面 x+ y+ z = 1 被三坐标面所截三角形的整个 解: 记三角形域为, 取上侧, 则 边界, 方向如图所示.  = d y d z + d z d x + d xd y 利用对称性 = Dx y 3 d xd y 2 3 = Dxy 机动 目录 上页 下页 返回 结束

例2.T为柱面x2+y2=2y与平面y=z的交线，从Z 轴正向看为顺时针，计算7=y2dx+ydy+xzdz. 解：设Σ为平面z=y上被T所围椭圆域，且取下侧 则其法线方向余弦 cosa=0,cos B= 2 COSY=- 2 利用斯托克斯公式得 cosa cos B cos y ds=2∬0-as=0 公式目录上页下页返回结束

例2.  为柱面 与平面 y = z 的交线,从 z 轴正向看为顺时针, 计算 o z 2  y x 解: 设为平面 z = y 上被  所围椭圆域 , 且取下侧, 利用斯托克斯公式得 I d S   = = 0 则其法线方向余弦 cos cos  cos  x y  z      y xy xz 2  公式 目录 上页 下页 返回 结束