
第3章布尔代数基础 布尔代数得名于英国数学家乔治·布尔(George Boole,1815一1864)。为了研究人的 逻辑思维规律,他在1847年发表的《逻辑的数学分析》和1854年发表的《思维规律的研究》 两部著作中,首先提出了这种代数的基本概念和性质。此后,大约经过100年之久,于1938 年才由克劳德·香农(Claude E.Shannon)将布尔代数应用于电话继电器的开关电路中。至 今,布尔代数已成为分析和设计开关电路的重要数学工具。 本章不是从数学的角度去研究布尔代数,而是从应用的角度介绍布尔代数的一些基本 概念、基本定理、布尔函数的基本形式以及布尔函数的化简方法,以使读者掌握分析和设计 数字逻辑网络所需的数学工具。 3.1布尔代数的基本概念 计算机或其他数字系统无论多么复杂,它们都是由若干种最简单的、最基本的电路(如 门电路、触发器等)所组成的。这些电路的工作具有下列基本特点:从电路内部看,或是管 子导通,或是管子截止;从电路的输入输出看,或是电平的高低,或是脉冲的有无。由于这 种电路工作在开关状态,故称为开关电路。开关电路的工作状态可以用二元布尔代数来描 述,故二元布尔代数通常称为开关代数,或称为逻辑代数。因此,逻辑代数只是布尔代数的 一种特例。在本书中,如无特别说明,布尔代数均指逻辑代数。 3.1.1布尔变量及其基本运算 布尔代数和普通代数一样,用字母代表变量,布尔代数的变量称为布尔变量。和普通代 数不同的是,布尔变量只有两种取值,即0或1。并且,常量0和1没有普通代数中的0和1 的意义,它只表示两种可能,即命题的“假”和“真”,信号的“无”和“有”等。 布尔代数中的变量运算只有“或”“与”“非”3种基本运算,任何复杂的逻辑运算都可以 通过这3种基本运算来实现。 1.“或”运算 “或”运算又称为逻辑加。两个变量“或”运算的逻辑关系可表示为 F=A+B 式中,“+”号是“或”运算符。上式读作“F等于A或B”,或者“下等于A加B”,其意思是变 量A和B中只要有一者取值为1,则F就为1:若A和B全为0,则F为0。其逻辑关系可 以用真值表来描述,如表3.1所示
第3章 布尔代数基础 布尔代数得名于英国数学家乔治·布尔(GeorgeBoole,1815—1864)。为了研究人的 逻辑思维规律,他在1847年发表的《逻辑的数学分析》和1854年发表的《思维规律的研究》 两部著作中,首先提出了这种代数的基本概念和性质。此后,大约经过100年之久,于1938 年才由克劳德·香农(ClaudeE.Shannon)将布尔代数应用于电话继电器的开关电路中。至 今,布尔代数已成为分析和设计开关电路的重要数学工具。 本章不是从数学的角度去研究布尔代数,而是从应用的角度介绍布尔代数的一些基本 概念、基本定理、布尔函数的基本形式以及布尔函数的化简方法,以使读者掌握分析和设计 数字逻辑网络所需的数学工具。 3.1 布尔代数的基本概念 计算机或其他数字系统无论多么复杂,它们都是由若干种最简单的、最基本的电路(如 门电路、触发器等)所组成的。这些电路的工作具有下列基本特点:从电路内部看,或是管 子导通,或是管子截止;从电路的输入输出看,或是电平的高低,或是脉冲的有无。由于这 种电路工作在开关状态,故称为开关电路。开关电路的工作状态可以用二元布尔代数来描 述,故二元布尔代数通常称为开关代数,或称为逻辑代数。因此,逻辑代数只是布尔代数的 一种特例。在本书中,如无特别说明,布尔代数均指逻辑代数。 3.1.1 布尔变量及其基本运算 布尔代数和普通代数一样,用字母代表变量,布尔代数的变量称为布尔变量。和普通代 数不同的是,布尔变量只有两种取值,即0或1。并且,常量0和1没有普通代数中的0和1 的意义,它只表示两种可能,即命题的“假”和“真”,信号的“无”和“有”等。 布尔代数中的变量运算只有“或”“与”“非”3种基本运算,任何复杂的逻辑运算都可以 通过这3种基本运算来实现。 1.“或”运算 “或”运算又称为逻辑加。两个变量“或”运算的逻辑关系可表示为 F =A +B 式中,“+”号是“或”运算符。上式读作“F 等于A 或B”,或者“F 等于A 加B”,其意思是变 量A 和B 中只要有一者取值为1,则F 就为1;若A 和B 全为0,则F 为0。其逻辑关系可 以用真值表来描述,如表3.1所示
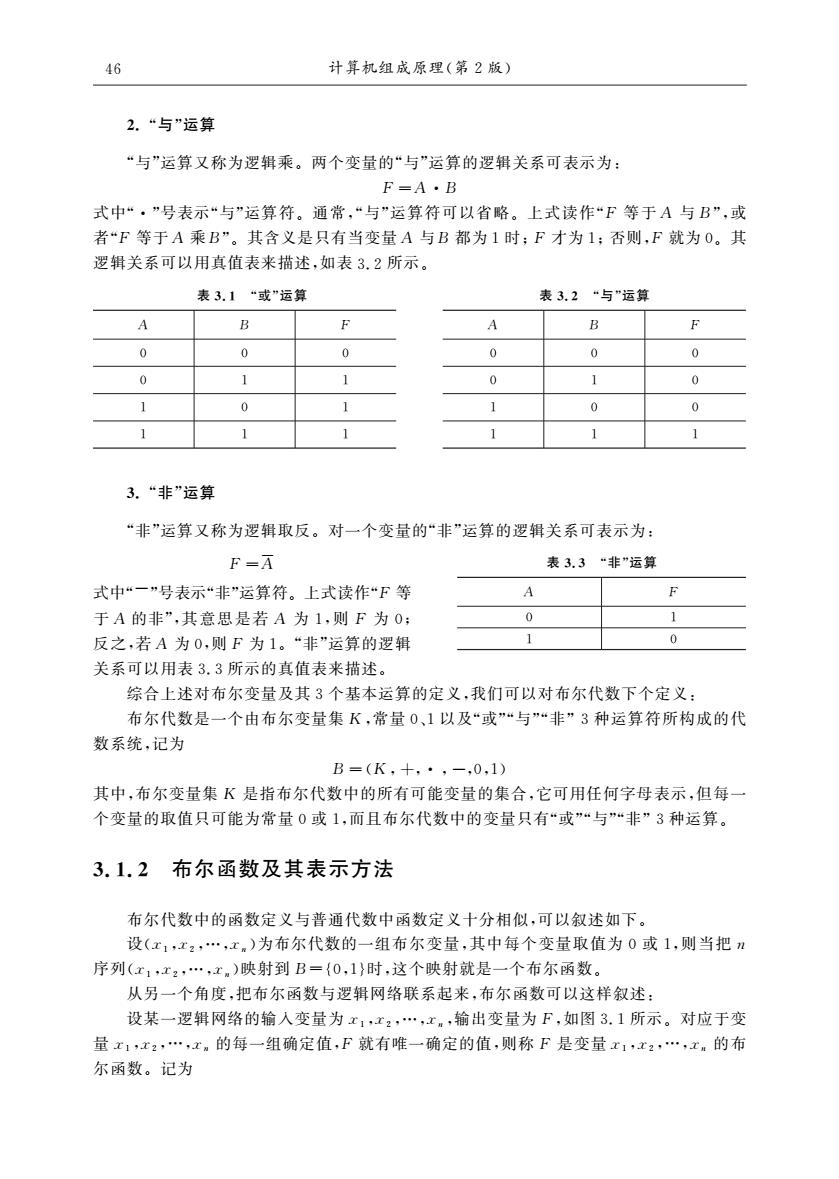
46 计算机组成原理(第2版) 2.“与”运算 “与”运算又称为逻辑乘。两个变量的“与”运算的逻辑关系可表示为: F=A.B 式中“”号表示“与”运算符。通常,“与”运算符可以省略。上式读作“F等于A与B”,或 者“F等于A乘B”。其含义是只有当变量A与B都为1时:F才为1:否则,F就为0。其 逻辑关系可以用真值表来描述,如表3.2所示 表31“或”运算 表3.2“与"运算 A B F A B F 0 0 0 0 0 0 0 1 0 1 0 1 1 0 0 1 3.“非”运算 “非”运算又称为逻辑取反。对一个变量的“非”运算的逻辑关系可表示为: F=万 表3.3“非”运算 式中“一”号表示“非”运算符。上式读作“℉等 A 于A的非”,其意思是若A为1,则F为0: 0 反之,若A为0,则F为1。“非”运算的逻辑 1 0 关系可以用表3.3所示的真值表米描述。 综合上述对布尔变量及其3个基本运算的定义,我们可以对布尔代数下个定义 布尔代数是一个由布尔变量集K,常量0、1以及“或”“与”“非”3种运算符所构成的代 数系统,记为 B=(K+,-,0,1) 其中,布尔变量集K是指布尔代数中的所有可能变量的集合,它可用任何字母表示,但每 个变量的取值只可能为常量0或1,而且布尔代数中的变量只有“或”“与”“非”3种运算。 3.1.2布尔函数及其表示方法 布尔代数中的函数定义与普通代数中函数定义十分相似,可以叙述如下。 设(x1江:,工)为布尔代数的一组布尔变量,其中每个变量取值为0或1,则当把, 序列(x1,x2,.,x.)映射到B={0,1}时,这个映射就是一个布尔函数。 从另一个角度,把布尔函数与逻辑网络联系起来,布尔函数可以这样叙述 设某一逻辑网铬的输入变量为x1,x2,.,x.,输出变量为F,如图3.1所示。对应于变 量x1x2.,x,的每一组确定值,F就有唯一确定的值,则称F是变量x1x,x的布 尔函数。记为
2.“与”运算 “与”运算又称为逻辑乘。两个变量的“与”运算的逻辑关系可表示为: F =A·B 式中“·”号表示“与”运算符。通常,“与”运算符可以省略。上式读作“F 等于A 与B”,或 者“F 等于A 乘B”。其含义是只有当变量A 与B 都为1时;F 才为1;否则,F 就为0。其 逻辑关系可以用真值表来描述,如表3.2所示。 表3.1 “或”运算 A B F 0 0 0 0 1 1 1 0 1 1 1 1 表3.2 “与”运算 A B F 0 0 0 0 1 0 1 0 0 1 1 1 3.“非”运算 “非”运算又称为逻辑取反。对一个变量的“非”运算的逻辑关系可表示为: F =A 式中“-”号表示“非”运算符。上式读作“F 等 于A 的非”,其意思是若 A 为1,则 F 为0; 反之,若A 为0,则F 为1。“非”运算的逻辑 关系可以用表3.3所示的真值表来描述。 表3.3 “非”运算 A F 0 1 1 0 综合上述对布尔变量及其3个基本运算的定义,我们可以对布尔代数下个定义: 布尔代数是一个由布尔变量集 K,常量0、1以及“或”“与”“非”3种运算符所构成的代 数系统,记为 B =(K,+,· ,-,0,1) 其中,布尔变量集 K 是指布尔代数中的所有可能变量的集合,它可用任何字母表示,但每一 个变量的取值只可能为常量0或1,而且布尔代数中的变量只有“或”“与”“非”3种运算。 3.1.2 布尔函数及其表示方法 布尔代数中的函数定义与普通代数中函数定义十分相似,可以叙述如下。 设(x1,x2,.,xn)为布尔代数的一组布尔变量,其中每个变量取值为0或1,则当把n 序列(x1,x2,.,xn)映射到B={0,1}时,这个映射就是一个布尔函数。 从另一个角度,把布尔函数与逻辑网络联系起来,布尔函数可以这样叙述: 设某一逻辑网络的输入变量为x1,x2,.,xn,输出变量为F,如图3.1所示。对应于变 量x1,x2,.,xn 的每一组确定值,F 就有唯一确定的值,则称F 是变量x1,x2,.,xn 的布 尔函数。记为 46 计算机组成原理(第2版)

第3章布尔代数基础 F=f(x1,x2,x.) 注意,布尔代数中函数的取值也只可能是0或1,这与普通代数 三思#一是不风你 布尔函数的表示方法有3种形式:布尔表达式、真值表利 图3.1布尔函数 卡诺图。这与普通代数中用公式、表格和图解这3种方法来表 示函数十分类似。 1.布尔表达式 布尔表达式是由布尔变量和“或”“与”“非”3种运算符所构成的式子,这是一种用公 式表示布尔函数的方法。例如,要表示这样一个函数关系:当两个变量A和B取值相同 时,函数取值为0;否则,函数取值为1。此函数称为异或函数,可以用下列布尔表达式来 表示: F=(A.B)=AB+AB 显然,只要将A和B的4种可能取值代入这表达式,验证是正确的。 与异或函数相反,当两个变量A和B取值相同时,函数取值为1;否则,函数取值为0 此函数称为同或函数。通常,异或运算用符号⊕表示:同或运算用⊙表示。因此,异或函 数、同或函数可分别表示成: F=IB+AB=A⊕B:F=不B+AB=A⊙B 2.真值表 真值表是由输入变量的所有可能取值组合及其对应的输出函数值所构成的表格,这是 一种用表格表示布尔函数的方法。例如,对于前面的异或函数,可以用表3.4所示的真值表 来表示。 表3.4异或函数的真值表 A B F 0 0 0 0 1 0 1 1 1 0 真值表中的变量为两个,共有2种取值组合,所以该表由4行组成。当变量为”个时。 真值表就由2”行组成。显然,随着变量数日的增加,真值表的行数将急剧增加。因此,一般 当变量数目不超过4个时,用真值表表示函数比较方便。 3.卡诺图 卡诺图是由表示逻辑变量的所有可能取值组合的小方格所构成的图形,如图3.2所示。 图中分别表示了二变量及三变量的卡诺图。 利用卡诺图,可以很方便地表示一个函数。只要在那些使函数值为1的变量取值组合
F =f(x1,x2,.,xn) 图3.1 布尔函数 注意,布尔代数中函数的取值也只可能是0或1,这与普通代数 是不同的。 布尔函数的表示方法有3种形式:布尔表达式、真值表和 卡诺图。这与普通代数中用公式、表格和图解这3种方法来表 示函数十分类似。 1.布尔表达式 布尔表达式是由布尔变量和“或”“与”“非”3种运算符所构成的式子,这是一种用公 式表示布尔函数的方法。例如,要表示这样一个函数关系:当两个变量 A 和B 取值相同 时,函数取值为0;否则,函数取值为1。此函数称为异或函数,可以用下列布尔表达式来 表示: F =f(A,B)=AB +AB 显然,只要将A 和B 的4种可能取值代入这表达式,验证是正确的。 与异或函数相反,当两个变量A 和B 取值相同时,函数取值为1;否则,函数取值为0。 此函数称为同或函数。通常,异或运算用符号表示;同或运算用☉表示。因此,异或函 数、同或函数可分别表示成: F =AB +AB =A B;F =AB +AB =A☉B 2.真值表 真值表是由输入变量的所有可能取值组合及其对应的输出函数值所构成的表格,这是 一种用表格表示布尔函数的方法。例如,对于前面的异或函数,可以用表3.4所示的真值表 来表示。 表3.4 异或函数的真值表 A B F 0 0 0 0 1 1 1 0 1 1 1 0 真值表中的变量为两个,共有2 2 种取值组合,所以该表由4行组成。当变量为n 个时, 真值表就由2 n 行组成。显然,随着变量数目的增加,真值表的行数将急剧增加。因此,一般 当变量数目不超过4个时,用真值表表示函数比较方便。 3.卡诺图 卡诺图是由表示逻辑变量的所有可能取值组合的小方格所构成的图形,如图3.2所示。 图中分别表示了二变量及三变量的卡诺图。 利用卡诺图,可以很方便地表示一个函数。只要在那些使函数值为1的变量取值组合 第3章 布尔代数基础 47

48 计算机组成原理(第2版) 所对应的小方格上标记1,便得该函数的卡诺图。例如,对于异或函数,可以用图3.3所示 的卡诺图来表示。 00011110 00010 0000010110100 001 10111 1001011111101 001 (a)二变量 ()三变量 10 图3.2卡诺图 图3.3异或函数的卡诺图 卡诺图可以看成是真值表的重新排列,真值表的每一行用一个小方格来表示。当变量 为两个时,真值表有4行,相应的卡诺图有4个方格:当变量为”个时,卡诺图有2”个方 格。卡诺图的这种方格排列方式比直值表更紧凑,而且便于进行函数的化简。 3.1.3布尔函数的“相等”概念 布尔函数和普通代数一样,也有函数相等的问题。两个函数相等的定义如下。 设有两个布尔函数 F=f(x1x.) G=g(x1x2.,x) 其变量都为x1x2,x。如果对应于变量x1x2,x。的任何一组变量取值,F和G的 值都相同,则称F和G是相等的,记为F一G。 显然,若两个布尔函数相等,则它们的真值表一定相同:反之,若两个布尔函数的真值 表完全相同,则此两个函数相等。因此,要证明两个布尔函数是否相等,只要分别列出它们 的真值表,看其是否相同。 例如,已知下列两个函数 F=ry.G=r+v 列出F和G的真值表,如表3.5所示。由表可知,它们的真值表完全相同,故F和G是相 等的,即有 ry=T+y 表3.5F=灯和G=F+了的真值表 F=- G=+ 0 0 0 1 1 0 1 0 1 1 1 0 0 1 1 0 0
所对应的小方格上标记1,便得该函数的卡诺图。例如,对于异或函数,可以用图3.3所示 的卡诺图来表示。 图3.2 卡诺图 图3.3 异或函数的卡诺图 卡诺图可以看成是真值表的重新排列,真值表的每一行用一个小方格来表示。当变量 为两个时,真值表有4行,相应的卡诺图有4个方格;当变量为n 个时,卡诺图有2 n 个方 格。卡诺图的这种方格排列方式比真值表更紧凑,而且便于进行函数的化简。 3.1.3 布尔函数的“相等”概念 布尔函数和普通代数一样,也有函数相等的问题。两个函数相等的定义如下。 设有两个布尔函数 F =f(x1,x2,.,xn) G =g(x1,x2,.,xn) 其变量都为x1,x2,.,xn。如果对应于变量x1,x2,.,xn 的任何一组变量取值,F 和G 的 值都相同,则称F 和G 是相等的,记为F=G。 显然,若两个布尔函数相等,则它们的真值表一定相同;反之,若两个布尔函数的真值 表完全相同,则此两个函数相等。因此,要证明两个布尔函数是否相等,只要分别列出它们 的真值表,看其是否相同。 例如,已知下列两个函数 F =xy, G =x- +y - 列出F 和G 的真值表,如表3.5所示。由表可知,它们的真值表完全相同,故F 和G 是相 等的,即有 xy=x- +y - 表3.5 F=xy 和G=x -+y - 的真值表 x y xy F=xy x - y - G=x -+y - 0 0 0 1 1 1 1 0 1 0 1 1 0 1 1 0 0 1 1 1 1 1 1 1 0 0 0 0 48 计算机组成原理(第2版)

第3章布尔代数基础 49 3.2布尔代数的公式、定理和规则 3.2.1布尔代数的基本公式 根据布尔变量的取值只有0和1,以及布尔变量仅有的3种运算的定义,不难推出下列 基本公式。 (1)交换律 A+B=B+A A·B=B·A (2)结合律 (A+B)+C=A+(B+C) (A·B)·C=A·(B·C) (3)分配律 A·(B+C)=A·B+A·C A+B·C=(A+B)(A+C) (4)0-1律 A+0=A A+1=1 A·0=0 A.1=A (5)互补律 A+A=1 A.A=0 (6)等幂律 A+A=A A·A=A (7)吸收律 (A+AB=A A+不B=A+B (A(A+B)-A A(A+B)=AB (8)对合律(双重否定律) A-A 以上是布尔代数的基本公式。其中交换律、结合律、分配律、0-1律、互补律和对合律可 以作为布尔代数的公理。公理是代数系统的基本出发点,是客观存在的抽象,它无须证明
3.2 布尔代数的公式、定理和规则 3.2.1 布尔代数的基本公式 根据布尔变量的取值只有0和1,以及布尔变量仅有的3种运算的定义,不难推出下列 基本公式。 (1)交换律 A +B =B +A A·B =B·A (2)结合律 (A +B)+C =A + (B +C) (A·B)·C =A·(B·C) (3)分配律 A·(B +C)=A·B +A·C A +B·C =(A +B)(A +C) (4)0-1律 A +0=A A +1=1 A·0=0 A·1=A (5)互补律 A +A =1 A·A =0 (6)等幂律 A +A =A A·A =A (7)吸收律 A +AB =A A +AB =A +B A(A +B)=A A(A +B)=AB (8)对合律(双重否定律) A = =A 以上是布尔代数的基本公式。其中交换律、结合律、分配律、0-1律、互补律和对合律可 以作为布尔代数的公理。公理是代数系统的基本出发点,是客观存在的抽象,它无须证明, 第3章 布尔代数基础 49