
一、劳斯判据 → 基于方程式的根与系数的关系而建立的 1、必要条件:设系统的特征方程为: ans"anis"+.+as+ao =O y+as-1++4s+4=(S-S)S-S2).(S-S,)=0 an an an 17/88
1、必要条件:设系统的特征方程为: 17/88 一、劳斯判据 1 1 1 0 0 n n n n a s a s a s a − + + + + = − 1 0 1 1 1 2 ( )( ) ( ) 0 n n n n n n n a a a s s s S S S S S S a a a − − + + + + = − − − = 基于方程式的根与系数的关系而建立的
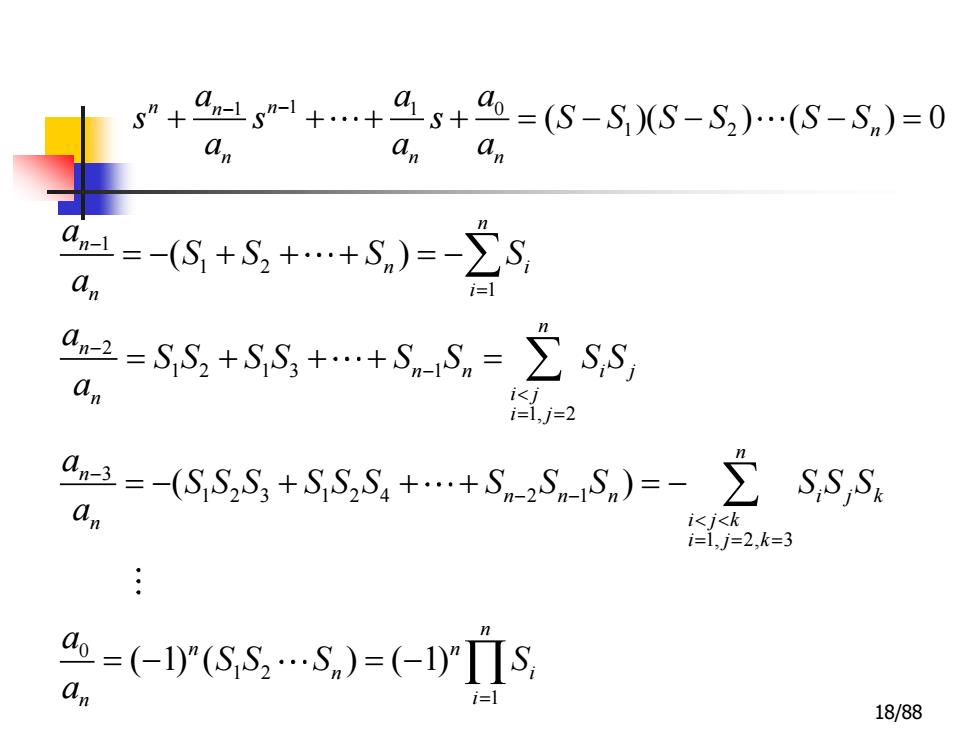
s”+ s41+.+4s+4=(S-SS-S).(S-S,)=0 a an an =-6+S,++S)=-2s an 9n2=SS2+SS;++S-S,=>SS a 1< i=1,j=2 =-(SS,S;+SS++SS)=-> SSS an 1<j<k i=1,j=2,k=3 =(-1(S,S2.S)=(-10ΠS an 18/88
18/88 1 1 2 1 2 1 2 1 3 1 1, 2 3 1 2 3 1 2 4 2 1 1, 2, 3 0 1 2 1 ( ) ( ) ( 1) ( ) ( 1) n n n i n i n n n n i j n i j i j n n n n n i j k n i j k i j k n n n n i n i a S S S S a a S S S S S S S S a a S S S S S S S S S S S S a a S S S S a − = − − = = − − − = = = = = − + + + = − = + + + = = − + + + = − = − = − 1 0 1 1 1 2 ( )( ) ( ) 0 n n n n n n n a a a s s s S S S S S S a a a − − + + + + = − − − =

由上式可知,要使全部特征根S,S,.Sn均具有负实部, 必须满足如下2个条件: (1)特征方程的各项系数a(0,.,n)不等于0; (2)特征方程的各项系数a,(i=0,.,n)符号都相同,一般a,>0 2.充要条件:Routh阵列中第一列所有项均为正,且值不为0 19/88
由上式可知,要使全部特征根 均具有负实部, 必须满足如下2个条件: (1) 特征方程的各项系数ai (i=0,.,n)不等于0; (2)特征方程的各项系数ai (i=0,.,n)符号都相同,一般ai>0 2.充要条件:Routh阵列中第一列所有项均为正,且值不为0 19/88 1 2 n S S S

Routh阵列表 S an an-2 a-4an-6. 4=0020,0 B Aan-3-Aa- S- an-1 an-3 an-5 0n-7. a 4 S-2 A 4 A A4. 4=8000 B= 4-5-414 Su-3 B B an-1 B4. 4-00600 an- S2 D D E 系数A、B的计算,一直进行到其余A、B.等于0为止。 S E 20/88
Routh阵列表 20/88 1 1 2 1 2 3 4 3 1 2 3 4 2 1 2 1 1 0 1 n n n n n n n n n n n n a a a a a a a a A A A A B B B B D D E F − − − − -2 -4 -6 -3 -5 -7 S S S S S S S 1 2 3 1 3 1 1 1 1 1 1 4 5 1 5 1 3 2 1 1 1 6 7 1 7 1 4 3 1 1 n n n n n n n n n n n n n n n n n n n n n a a a a A a A a A B a A a a a a A a a A A B a A a a a a A a a A A B a A − − − − − − − − − − − − − − − − − − − − = = − − = = − − = = 2 2 3 系数Ai、Bi的计算,一直进行到其余Ai、Bi .等于0为止

系统稳定的充要条件:Rouh阵列中第一列所有项均为正。 且:Routh阵列中第一列的系数符号改变的次数等于实部为 正的特征根数。 例1.设控制系统的特征方程式为: s4+8s3+17s2+16s+5=0 试判断系统的稳定性。 21/88
21/88 系统稳定的充要条件:Routh阵列中第一列所有项均为正。 且:Routh阵列中第一列的系数符号改变的次数等于实部为 正的特征根数。 例1.设控制系统的特征方程式为: 试判断系统的稳定性。 4 3 2 s s s s + + + + 8 17 16 5=0