
第二章系统的数学模型 基础章节 传递函数 模型: 对建模的要求:准确、简化 状态空间表达式 基本概念:1.微分方程;2.传递函数;3.方框图;4.相似原理
第二章 系统的数学模型 对建模的要求:准确、简化 传递函数 状态空间表达式 基本概念:1.微分方程;2.传递函数;3.方框图;4.相似原理 模型: 基础章节

本章内容 一系统数学模型基本概念,应用机械动力学、电子 学等基础知识建立系统数学模型的基本方法,典型例子; 二传递函数的基本概念,其数学、物理意义,求取 方法,输入输出信号与传递函数的关系; 三系统方框图,闭环控制系统及其传递函数,方框 图的等效简化,工程中典型的机、电系数的传递函数
一.系统数学模型基本概念,应用机械动力学、电子 学等基础知识建立系统数学模型的基本方法,典型例子; 二.传递函数的基本概念,其数学、物理意义,求取 方法,输入输出信号与传递函数的关系; 三.系统方框图,闭环控制系统及其传递函数,方框 图的等效简化,工程中典型的机、电系数的传递函数。 本章内容

§2.1系统的微分方程 线性系统与非线性系统: 1.线性 ao(t)+a(t)+azxo(1)=x,(t) 特性:叠加原理,多个输入量同时作用产生的响应,可单 个处理叠加: (+x=Asin(@t) 2.非线性: x+x+x+x3=0 实际只是一定的工作范围内,保持线性关系。 特点:不能叠加线性化(一定的范围内)
§2.1 系统的微分方程 一.线性系统与非线性系统: 1.线性 特性:叠加原理,多个输入量同时作用产生的响应,可单 个处理 叠加. 2.非线性: 实际只是一定的工作范围内,保持线性关系。 特点:不能叠加 线性化(一定的范围内) a x t a x t a x t x t 0 0 1 0 2 0 ( ) + + = ( ) ( ) i ( ) ( ) ( ) 2 3 sin 0 x x x A t xxxx + + = + + + =

二线性系统微分方程的列写 设线性定常系统的输入为x(输出为 (t) 则描述系统输入一输出动态关系的微分方程为: anx)m(t))+an-xm-(t0)+.+ax()+a,x(t) =bnxm()+bn-1xm-()++b元(()+bx(t) (n≥m)
二.线性系统微分方程的列写 设线性定常系统的输入为 ,输出为 , 则描述系统输入—输出动态关系的微分方程为: x t i ( ) x t 0 ( ) ( ) ( ) ( ) ( ) ( ) ( 1) 0 1 0 1 0 0 0 ( ) ( 1) 1 1 0 ( ) ( ) . ( ) ( ) . ( ) n n n n m m m i m i i i a x t a x t a x t a x t b x t b x t b x t b x t n m − − − − + + + + = + + + +
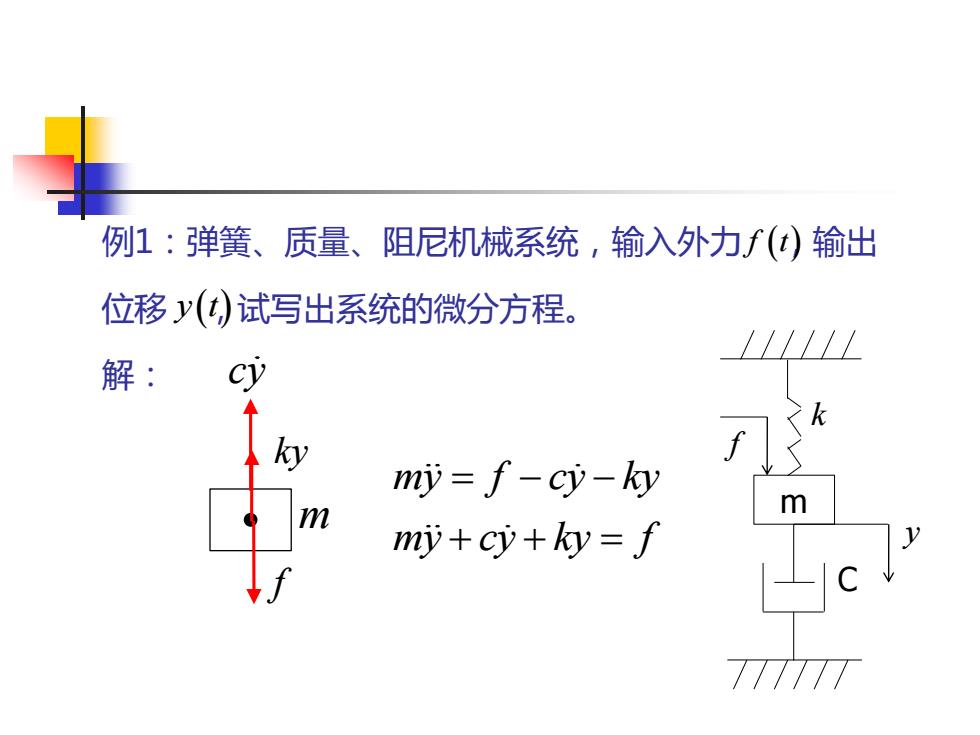
例1:弹簧、质量、阻尼机械系统,输入外力f()输出 位移y()试写出系统的微分方程。 解: my=f-cy-ky m mi+cy+ky=f
例1:弹簧、质量、阻尼机械系统,输入外力 ,输出 位移 ,试写出系统的微分方程。 解: f t( ) y t( ) my f cy ky my cy ky f = − − + + = m C y f k m cy f ky