
第五章系统的稳定性 设计控制系统时应满足多种性能指标,但最重要的技术要求是系统 必须稳定。因为稳定性是系统能正常工作的首要条件,只有工作稳定才 能进一步讨论其他性能指标。 分析系统的稳定性是控制理论的最重要组成部分之一。 控制理论对于判断一个线性定常系统是否稳定提供了多种方法。 本章着重介绍几种常用的稳定判据,以及提高系统稳定性的方法。 本章内容 一、介绍系统稳定性的基本概念,判断系统稳定性的基本 明 出发点 确 二、系统稳定的充分必要条件 (三、代数判据(Routh、Hurwitz判据) 重点 四、lyquist判据的基本原理和方法,Bode判据 掌握 五、相对稳定性的概念 六、掌握相位裕量和幅值裕量的概念及计算方法
第五章 系统的稳定性 设计控制系统时应满足多种性能指标,但最重要的技术要求是系统 必须稳定。因为稳定性是系统能正常工作的首要条件,只有工作稳定才 能进一步讨论其他性能指标。 分析系统的稳定性是控制理论的最重要组成部分之一。 控制理论对于判断一个线性定常系统是否稳定提供了多种方法。 本章着重介绍几种常用的稳定判据,以及提高系统稳定性的方法。 本章内容 一、介绍系统稳定性的基本概念,判断系统稳定性的基本 出发点 二、系统稳定的充分必要条件 三、代数判据(Routh、Hurwitz 判据) 四、Nyquist 判据的基本原理和方法,Bode 判据 五、相对稳定性的概念 六、掌握相位裕量和幅值裕量的概念及计算方法 明 确 重点 掌握
§5-1.系统稳定性的初步概念 若一个系统受到扰动,偏离了原来的平衡状态,而当扰动取消后 经过充分长的时间,这个系统又能够以一定的精度逐渐恢复到原来的状 态,则称系统是稳定的,否则不稳定。 倒摆 b 小球处在a点时,是稳定平衡点,因为作用于小球上的有限干扰力 消失后,小球总能回到a点,而小球处于b、c点时,为不平衡点,因为 只要有千扰力作用与小球时,小球便不再回到b或c。 控制系统在实际运行过程中,总会受到外部和内部的扰动,如火炮 射击时,施加给随动系统的冲击负载:雷达天线跟踪时,突然遇到阵风。 如果系统不稳定,就会在任何微小的扰动作用下偏离原来的平衡状态, 并随时间的推移而发散。 因此,如何分析系统的稳定性,并提出保证系统稳定的措施,是自 动控制的基本任务
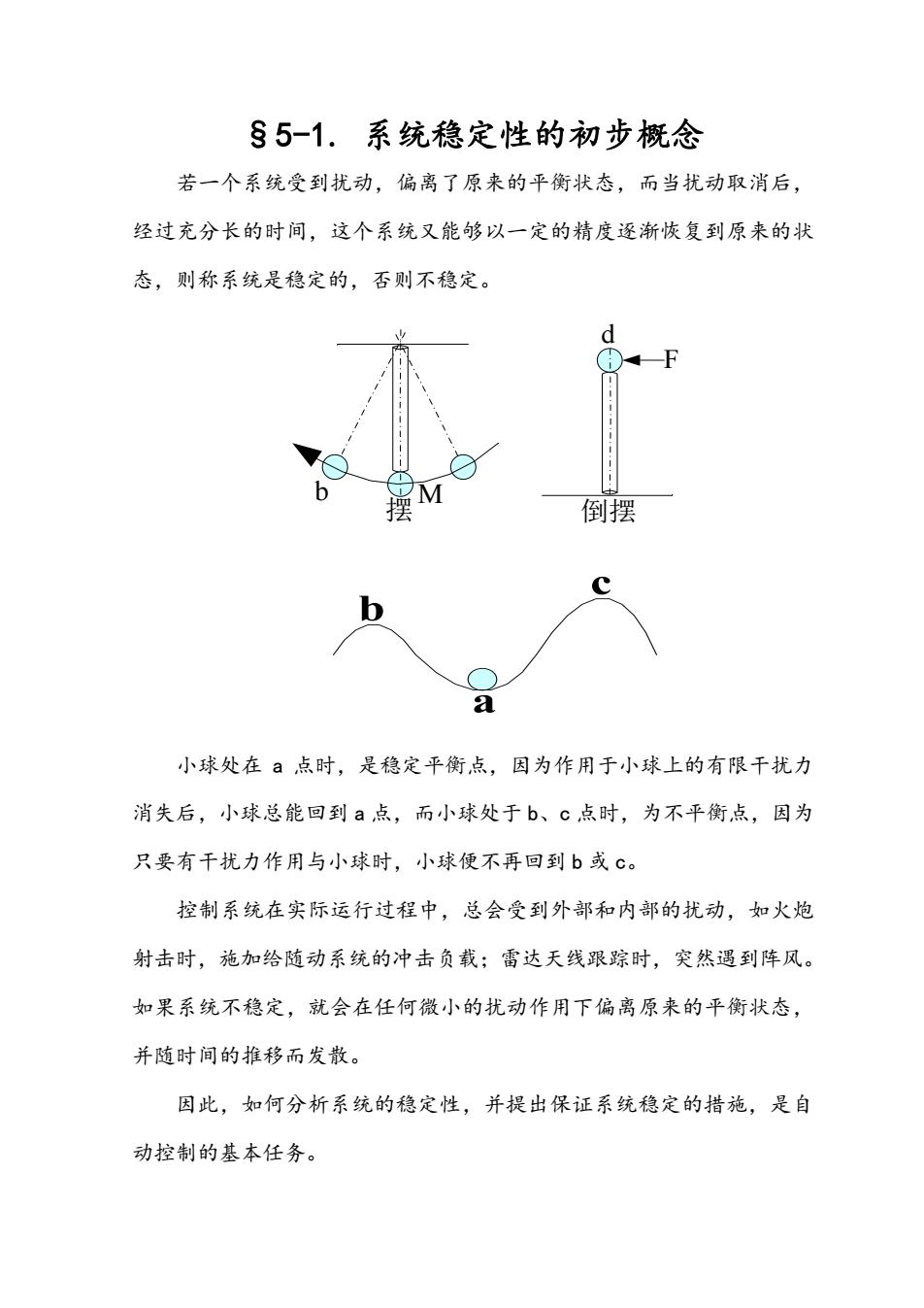
§5-1. 系统稳定性的初步概念 若一个系统受到扰动,偏离了原来的平衡状态,而当扰动取消后, 经过充分长的时间,这个系统又能够以一定的精度逐渐恢复到原来的状 态,则称系统是稳定的,否则不稳定。 b M 摆 F 倒摆 d c a b 小球处在 a 点时,是稳定平衡点,因为作用于小球上的有限干扰力 消失后,小球总能回到 a 点,而小球处于 b、c 点时,为不平衡点,因为 只要有干扰力作用与小球时,小球便不再回到 b 或 c。 控制系统在实际运行过程中,总会受到外部和内部的扰动,如火炮 射击时,施加给随动系统的冲击负载;雷达天线跟踪时,突然遇到阵风。 如果系统不稳定,就会在任何微小的扰动作用下偏离原来的平衡状态, 并随时间的推移而发散。 因此,如何分析系统的稳定性,并提出保证系统稳定的措施,是自 动控制的基本任务

一、定义 定义:上述2个实例说明系统的稳定反映在干扰消失后的过渡过程的 性质上,因此,控制系统的稳定性可以这样定义。 若控制系统在任何足够小的初始偏差的作用下,其过渡过程随时间 的推移,逐渐衰减至零,具有恢复原平衡状态的性能,则称该系统稳定 .(0 4x0 4x0 系统自由振荡输出三种情况 即:若线性系统受到扰动的作用而使输出量o()发生偏差,产生 △加()。扰动消失后,经过足够长的时间,改偏差的绝对值小于给定 的正值E。limAr,()≤6,则系统渐近稳定,否则不稳定。如果系统在任 意初始条件下都保持渐近稳定,则称为大范围内渐近稳定。 渐近稳定:m0→0(一般所讲的线性系统的稳定性,就是渐近 稳定性) 注意事项: 1.线性系统不稳定现象发生与否,取决于系统内部条件,而与输入 无关。 线性系统的稳定性只取决于系统本身的结构参数,而与输入无关(非 线性系统的稳定性与输入有关) 2.系统发生不稳定现象必有适当的反馈作用
一、定义 定义:上述 2 个实例说明系统的稳定反映在干扰消失后的过渡过程的 性质上,因此,控制系统的稳定性可以这样定义。 若控制系统在任何足够小的初始偏差的作用下,其过渡过程随时间 的推移,逐渐衰减至零,具有恢复原平衡状态的性能,则称该系统稳定。 xo(t) xo(t) xo(t) 系统自由振荡输出三种情况 即:若线性系统受到扰动的作用而使输出量 xo(t)发生偏差,产生 △ xo(t)。扰动消失后,经过足够长的时间,改偏差的绝对值小于给定 的正值ε。 0 lim ( ) t x t ,则系统渐近稳定,否则不稳定。如果系统在任 意初始条件下都保持渐近稳定,则称为大范围内渐近稳定。 渐近稳定: 0 lim ( ) 0 t x t (一般所讲的线性系统的稳定性,就是渐近 稳定性) 注意事项: 1.线性系统不稳定现象发生与否,取决于系统内部条件,而与输入 无关。 线性系统的稳定性只取决于系统本身的结构参数,而与输入无关(非 线性系统的稳定性与输入有关) 2.系统发生不稳定现象必有适当的反馈作用
X,() EG) Xo(s) 图5.1闭环方框图 3.控制系统理论中所讨论的稳定性其实都是指自由振荡f的稳定性, 即:讨论输入为0,系统仅存在有初始状态不为0时的稳定性,即讨论系 统自由振荡是收敛的还是发散的。 至于机械工程系统,往往用激励或加外力的方发施以强迫振动或运 动,因而造成系统共振(或谐振)或偏离平衡位置越来越远,这不是控 制理论所要求讨论的稳定性。 二、稳定条件 一般反馈系统的传函为: G(s) G)=1+G)H X,(s) 85)G回 Xo(s) H(s) 图5.2一般反馈系统 设分母=0,可得出系统的特征方程: 1+G(s-Hs)=0 (一)稳定条件: 系统的稳定性决定于特征方程。只要指出特征方程的根落在[S]复平 面的左半部分,系统即是稳定的
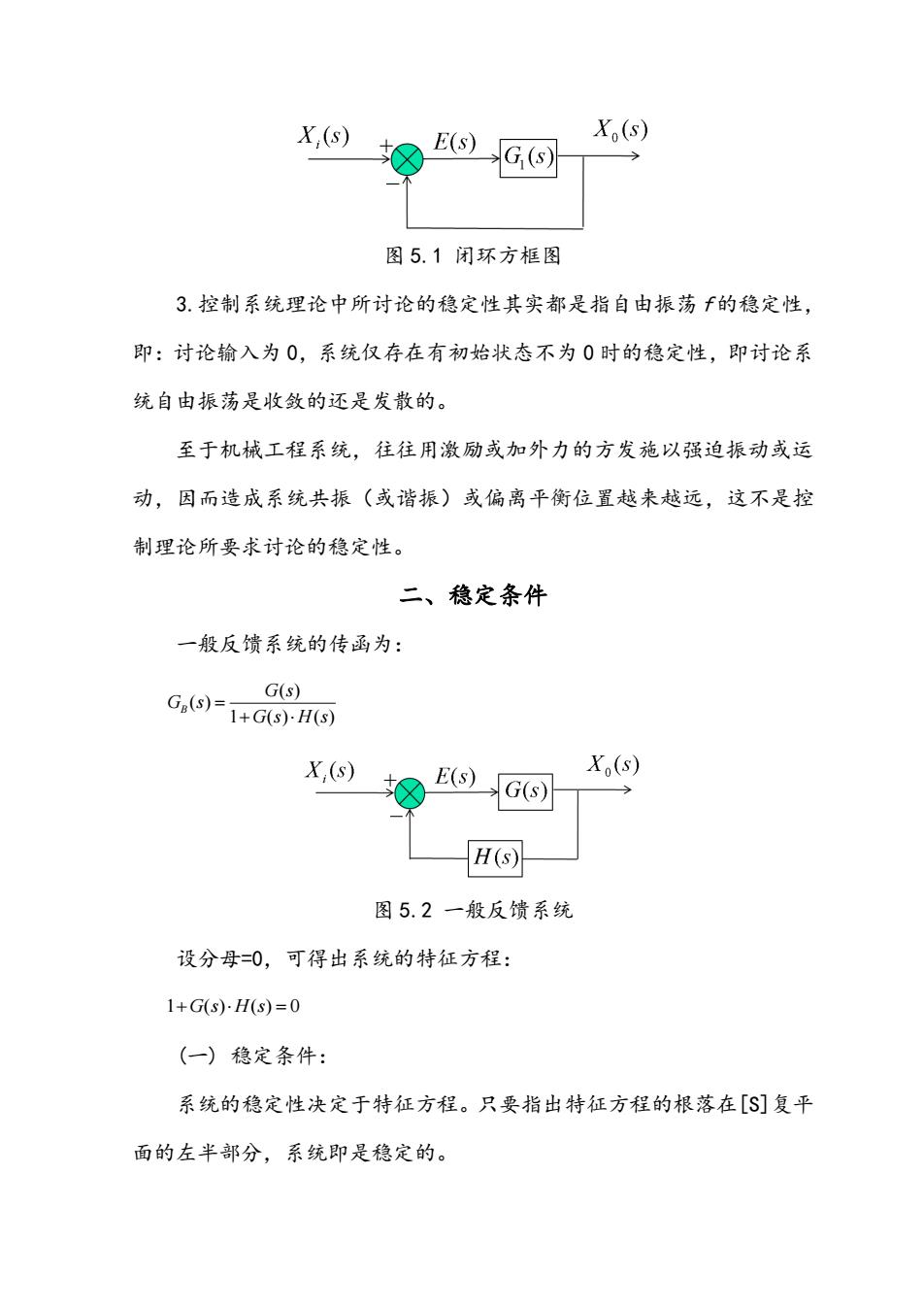
图 5.1 闭环方框图 3.控制系统理论中所讨论的稳定性其实都是指自由振荡 f 的稳定性, 即:讨论输入为 0,系统仅存在有初始状态不为 0 时的稳定性,即讨论系 统自由振荡是收敛的还是发散的。 至于机械工程系统,往往用激励或加外力的方发施以强迫振动或运 动,因而造成系统共振(或谐振)或偏离平衡位置越来越远,这不是控 制理论所要求讨论的稳定性。 二、稳定条件 一般反馈系统的传函为: ( ) ( ) 1 ( ) ( ) B G s G s G s H s 图 5.2 一般反馈系统 设分母=0,可得出系统的特征方程: 1 ( ) ( ) 0 G s H s (一) 稳定条件: 系统的稳定性决定于特征方程。只要指出特征方程的根落在[S]复平 面的左半部分,系统即是稳定的

(二)线性稳定的条件: 设线性系统在初始条件为0时,输入一个理想单位脉冲函数6(t), 这时系统的输出是单位脉冲响应,这相当于系统在扰动信号作用下,输 出信号偏离元平衡点的情形。 若线性系统的单位脉冲响应函数(),随时间的推移趋于0,即: m)=0,则系统稳定:若m0)=0,则系统不稳定。 若x()→C或等幅振荡→临界稳定状态。 但由于参数变化等原因,等幅振荡不能维持→不稳定。 工程意义上的不稳定 60工+8仞=1 火0-品5品品含品 HS-S 0=2ce 可知,要满足limx)=0,只有当特征根全部为负实部。 系统稳定的充要条件:稳定系统的特征方程根必须全部具有负实部, 反之,若特征根中有一个以上具有正实部时,则系统必不稳定。 或系统传函但的极,点全部位于[S]复平面的左半部。若有部分闭 X,(s) 环极点位于虚轴上,而其余极,点全在[S]平面左半部时,便会出现前边所 述的临界稳定性状态,系统处于等幅振荡状态,从设计角度不可取(很 容易转化为不稳定系统)
(二) 线性稳定的条件: 设线性系统在初始条件为 0 时,输入一个理想单位脉冲函数б(t), 这时系统的输出是单位脉冲响应,这相当于系统在扰动信号作用下,输 出信号偏离元平衡点的情形。 若线性系统的单位脉冲响应函数 0 x t() ,随时间的推移趋于 0,即: 0 lim ( ) 0 t x t ,则系统稳定;若 0 lim ( ) t x t ,则系统不稳定。 若 0 x t C ( ) 或等幅振荡 临界稳定状态。 但由于参数变化等原因,等幅振荡不能维持 不稳定。 工程意义上的不稳定 ()t L t [ ( )] 1 1 2 0 1 2 1 ( ) n n i n i i C C C C X s S S S S S S S S 0 1 ( ) i n S t i i x t C e 可知,要满足 0 lim ( ) 0 t x t ,只有当特征根全部为负实部。 系统稳定的充要条件:稳定系统的特征方程根必须全部具有负实部, 反之,若特征根中有一个以上具有正实部时,则系统必不稳定。 或系统传函 0 ( ) ( ) i X s X s 的极点全部位于[S]复平面的左半部。若有部分闭 环极点位于虚轴上,而其余极点全在[S]平面左半部时,便会出现前边所 述的临界稳定性状态,系统处于等幅振荡状态,从设计角度不可取(很 容易转化为不稳定系统)。 L L -1