第三章系统的时域分析 数学模型→性能分析:稳、快、准等 时域分祈法 根轨迹法 频率法 、直观 微分方程+时间响应表达式 曲线 >性能分析 本章内容 系统的时间响应及其组成 (一) 典型的输入信号 三.对一阶、二阶、高阶系统的典型时间响应进行分析 四.分析性能指标(时域) (二)五.系统误差分析与计算
第三章 系统的时域分析 数学模型 性能分析:稳、快、准等 时域分析法 根轨迹法 频率法 微分方程 时间响应 表达式 曲线 性能分析 本章内容 一. 系统的时间响应及其组成 (一) 二. 典型的输入信号 三. 对一阶、二阶、高阶系统的典型时间响应进行分析 四. 分析性能指标(时域) (二) 五. 系统误差分析与计算 直 观
§3-1时域响应及典型输入信号 一时域响应 在输入信号的作用下,其输出随时间的变化过程x,①。 x(t)=L'[Xo(s)]=L'[G(s).x(s)] 1.瞬态响应和稳态响应: 输入引起的时间响应由瞬态和稳态两部分组成。 →y0 00 图3.1k-m-c系统 图3.2受力分析 例3.1:m+c少+y=Fsinot 细-点 f 2y-Fsinot 非齐次常微分方程的完全解: ∴J0=Aesin(o,V1-5i+0)+Bsin(or+p)) 有由衰减震荡受迫振动 瞬态响应 稳态响应 瞬态响应一系统在某一输入信号的作用下,其输出量从初始状态 →稳定状态的响应过程。(过渡过程)
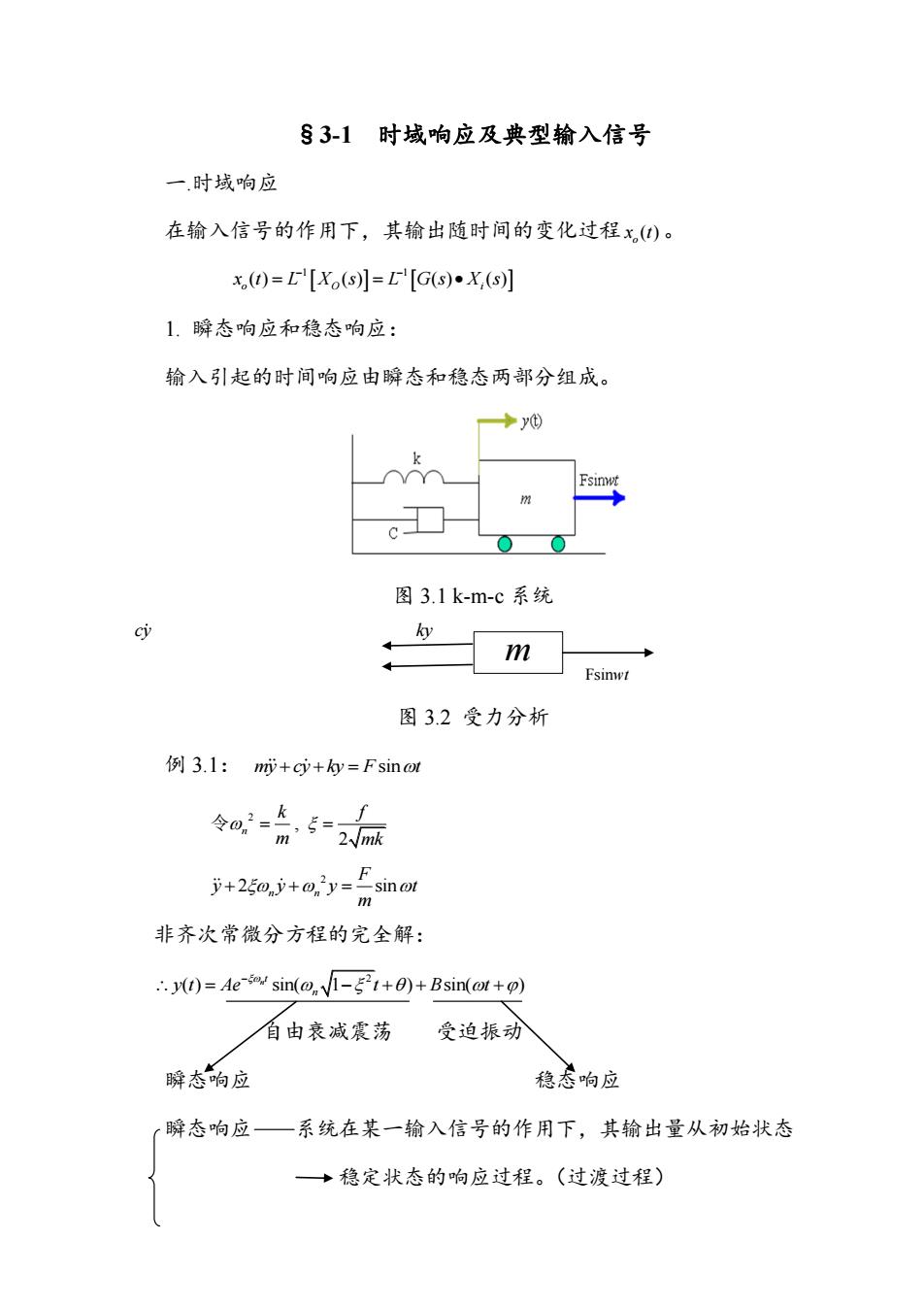
§3-1 时域响应及典型输入信号 一.时域响应 在输入信号的作用下,其输出随时间的变化过程 () o x t 。 1 1 ( ) ( ) ( ) ( ) o O i x t L X s L G s X s 1. 瞬态响应和稳态响应: 输入引起的时间响应由瞬态和稳态两部分组成。 图 3.1 k-m-c 系统 m Fsinwt 图 3.2 受力分析 例 3.1: my cy ky F t sin 2 , 2 n k f m mk 令 2 2 sin n n F y y y t m 非齐次常微分方程的完全解: 2 ( ) sin( 1 ) sin( ) n t n y t Ae t B t 自由衰减震荡 受迫振动 瞬态响应 稳态响应 瞬态响应 系统在某一输入信号的作用下,其输出量从初始状态 稳定状态的响应过程。(过渡过程) cy ky

稳态响应一当某一信号输入时,系统在时间趋于无穷大时的输出 状态。(静态) 2.系统的时域响应分析 在时间域内,研究各种形式的输入信号作用下,系统输出响应的时 间特征,即对系统施加一定形式的输入信号,然后研究系统的输出量随 时间的变化规律。 二、典型的输入信号 1.阶跃函数(图3.3) 0=6e0 a=1时,单位阶跃函数 图3.3阶跃函数 图3.4斜坡函数 2.斜坡函数(图3.4) 0=任8 a=1时,单位斜坡函数 3.加速度函数(图3.5) 1<0 a=)时,单位加速度函数 a/to +1 图3.5加速度函数 图3.6脉冲函数
稳态响应 当某一信号输入时,系统在时间趋于无穷大时的输出 状态。(静态) 2. 系统的时域响应分析 在时间域内,研究各种形式的输入信号作用下,系统输出响应的时 间特征,即对系统施加一定形式的输入信号,然后研究系统的输出量随 时间的变化规律。 二、典型的输入信号 1.阶跃函数(图 3.3) , 0 ( ) 0, 0 i a t x t t a 1 时,单位阶跃函数 xi t a xi t 图 3.3 阶跃函数 图 3.4 斜坡函数 2.斜坡函数(图 3.4) 0 ( ) 0, 0 i at t x t t , a 1 时,单位斜坡函数 3. 加速度函数(图 3.5) 2 , 0 ( ) 0, 0 i at t x t t 1 2 a 时,单位加速度函数 xi t xi t t0 a/t0 图 3.5 加速度函数 图 3.6 脉冲函数

4.脉冲函数(图3.6) lima,0<t<t x(0={6 a=1时,单位脉冲函数 0,t<0或1>6 5.正弦函数(图3.7) 40-8 X(s)=X(s)G(s)当X()=6()→0 :G(s)=X(S)=[x(]x)—脉冲响应函数 A! 图3.7正弦函数 输入信号的选择应视不同系统的具体工作状况而定: 1)若输入量是随时间逐渐变化的函数,如机床、雷达天线、火炮等, →选斜坡函数 2)若输入量是冲击量,如导弹发射等,→选脉冲函数 3)若输入量随时间往复运动,如机床振动,→选正弦函数 4)若输入量是突然变化的,如断电、合电等,→选阶跃函数
4. 脉冲函数(图 3.6) 0 0 lim , 0 ( ) 0, 0 0 i a t t x t t t t t 或 a 1 时,单位脉冲函数 5. 正弦函数(图 3.7) sin , 0 ( ) 0, 0 i a wt t x t t X s X s G s O i 当 X t t i r G s X s L x t O o x t o 脉冲响应函数 图 3.7 正弦函数 输入信号的选择应视不同系统的具体工作状况而定: 1)若输入量是随时间逐渐变化的函数,如机床、雷达天线、火炮等, 选斜坡函数 2)若输入量是冲击量,如导弹发射等, 选脉冲函数 3)若输入量随时间往复运动,如机床振动, 选正弦函数 4)若输入量是突然变化的,如断电、合电等, 选阶跃函数

§3.2一阶系统的时域响应 一阶系统:能够用一阶微分方程描述的系统。 典型形式:一阶惯性环节1 X,(s)Ts+1 一、一阶系统的单位阶跃响应M 11回11 X,)=5+1店+15s+7 +0=1-e7 x)=1-e7 表3-1单位阶跃响应 0T2T 3T 4T5T . x000.6320.8650.950.9820.993. 1 2 初始斜率= 1.865 图3.8一阶系统的单位阶跃响应曲线 可知: (1)一阶惯性系统总是稳定的,无振荡的。 (2)时间T上升到0.632的高度,反之,用实验方法测出曲线到达 63.2%高度点所用的=时间常数T
§3.2 一阶系统的时域响应 一阶系统:能够用一阶微分方程描述的系统。 典型形式:一阶惯性环节 0 ( ) 1 ( ) 1 i X s X s Ts 一、一阶系统的单位阶跃响应 M r ( ) 1 i x t 1 ( ) X s i s 1 2 1 1 ( 1) S T S T C X S Ts T s 0 1 1 1 ( ) 1 1 T X s Ts s s Ts 1 1 s 1 s T 0 ( ) 1 t T x t e 0 ( ) 1 t T x t e 表 3-1 单位阶跃响应 t 0 T 2T 3T 4T 5T . 0 x t() 0 0.632 0.865 0.95 0.982 0.993 . 1 图 3.8 一阶系统的单位阶跃响应曲线 可知: (1)一阶惯性系统总是稳定的,无振荡的。 (2)时间 T 上升到 0.632 的高度,反之,用实验方法测出曲线到达 63.2%高度点所用的 t=时间常数 T