《机械工程控制基础》课程授课教案（讲义）第二章 系统的数学模型

第二章 系统的数学模型 本章为基础章节 传递函数 建模：准确、简化 (状态空间表达式 基本概念：1微分方程；2.传递函数；3.方框图：4.相似原理 本章内容 一系统数学模型基本概念，应用机械动力学、电子学等基础知识建 立系统数学模型的基本方法，典型例子； 二传递函数的基本概念，其数学、物理意义，求取方法，输入输出 信号与传递函数的关系： 三，系统方框图，闭环控制系统及其传递函数，方框图的等效简化， 工程中典型的机、电系数的传递函数

第二章 系统的数学模型 本章为基础章节 传递函数 建模：准确、简化 状态空间表达式 基本概念：1.微分方程；2.传递函数；3.方框图；4.相似原理 本章内容 一.系统数学模型基本概念，应用机械动力学、电子学等基础知识建 立系统数学模型的基本方法，典型例子； 二.传递函数的基本概念，其数学、物理意义，求取方法，输入输出 信号与传递函数的关系； 三.系统方框图，闭环控制系统及其传递函数，方框图的等效简化， 工程中典型的机、电系数的传递函数

§2.1系统的微分方程 一线性系统与非线性系统： 1.线性：o 特性：叠加原理，多个输入量同时作用产生的响应，可单个处理→ 叠加 2.非线性： 实际只是一定的工作范围内，保持线性关系。 特点：不能叠加→线性化（一定的范围内）。 二线性系统微分方程的列写 设线性定常系统的输入为x(),输出为x(),则描述系统输入 一输出动态关系的微分方程为： anx(0）+an-xm-0）+.+a(0+a,0) =bxm()+bn-xm-(0)++()+bx()）(n之m) 例1.弹簧、质量、阻尼机械系统如图21所示，输入外力f0,输 出位移y),试写出系统的微分方程。 ACy m LjcT m 71777 ★f0) 图2.1k-m-c系统 受力分析图 解：对k-m-C系统进行受力分析，利用牛顿第二定律可得： i啦=f-少-y m+C少+y=f

§2.1 系统的微分方程 一.线性系统与非线性系统： 1.线性： T 特性：叠加原理，多个输入量同时作用产生的响应，可单个处理→ 叠加. 2.非线性： 实际只是一定的工作范围内，保持线性关系。 特点：不能叠加→线性化（一定的范围内）。 二.线性系统微分方程的列写 设线性定常系统的输入为 x t i   ，输出为 x t 0   ， 则描述系统输入 —输出动态关系的微分方程为：         ( ) ( 1) 0 1 0 1 0 0 0 ( ) ( 1) 1 1 0 ( ) ( ) . ( ) ( ) . ( ) n n n n m m m i m i i i a x t a x t a x t a x t b x t b x t b x t b x t n m               例 1. 弹簧、质量、阻尼机械系统如图 2.1 所示，输入外力 f t  ，输 出位移 y t  ，试写出系统的微分方程。 mcykyf t() 图 2.1 k-m-c 系统 受力分析图 解：对 k-m-c 系统进行受力分析，利用牛顿第二定律可得： my f cy ky my cy ky f      

例2.m-k振动系统，输入外力f),输出()、为()，求其动力学 方程。 05)0 m2(-) 手mm y m□0 图2.2m-k振动系统 受力分析图 解：对k-m-℃系统进行受力分析，利用牛顿第二定律可得： m=f-9-k(4-)(0) m=k(y-)(2) 三.系统非线性微分方程的线性化（略）P31页 四列写系统微分方程的一般步骤： 1.分析系统工作原理和系统中各变量间的关系，确定系统的输入量和 输出量。 2从系统的输入端开始，依物理定律，依次列写系统各元件的动力力 学方程，其中要考虑相邻元件间的负载效应。 3.将各方程式中的中间变量消去，求出输入量一输出量间的微分方程 4.在列写微分方程时，对非线性项进行线性化处理

例 2. m-k 振动系统，输入外力 f t  ，输出 y t 1  、 y t 2   ，求其动力学 方程。 k1 m1 k2 m2 f(t) y1(t) y2(t) m2 k y y 2 1 2    m1 f t() 1 ky k y y 2 1 2    图 2.2 m-k 振动系统 受力分析图 解：对 k-m-c 系统进行受力分析，利用牛顿第二定律可得：     1 1 1 2 1 2 2 2 2 1 2 .(1) .(2) m y f ky k y y m y k y y           三.系统非线性微分方程的线性化（略）P31 页 四.列写系统微分方程的一般步骤： 1.分析系统工作原理和系统中各变量间的关系，确定系统的输入量和 输出量。 2.从系统的输入端开始，依物理定律，依次列写系统各元件的动力力 学方程，其中要考虑相邻元件间的负载效应。 3.将各方程式中的中间变量消去，求出输入量—输出量间的微分方程 4.在列写微分方程时，对非线性项进行线性化处理

§2.2拉普拉斯(Laplace)变换 1熟悉L变换的定义 2.典型函数的拉氏变换 要求〈3.拉氏变换的基本原理 4部分分式展开式及待定系数法 5.查拉氏表 1方便求解，以时间表示的微分方程变为以S表示的代数方程 2.对零初始条件下，引入传递函数和传递矩阵的概念，直接在复（频） 域中研究系统的动态特性，以及对系统进行综合、校正，具实际意义。 一拉氏变换的定义 若)为t的函数，且0时，f)0,则f)的拉氏变换定义为： F(S)=[f()]=f()e“d 象函数 象函数 二.一些常用函数的拉氏变换 1单位阶跃函数40=01<0 11≥0 40 a 图2.3单位阶跃函数 F(S)=L[u()]=u"d=Sed=-se=

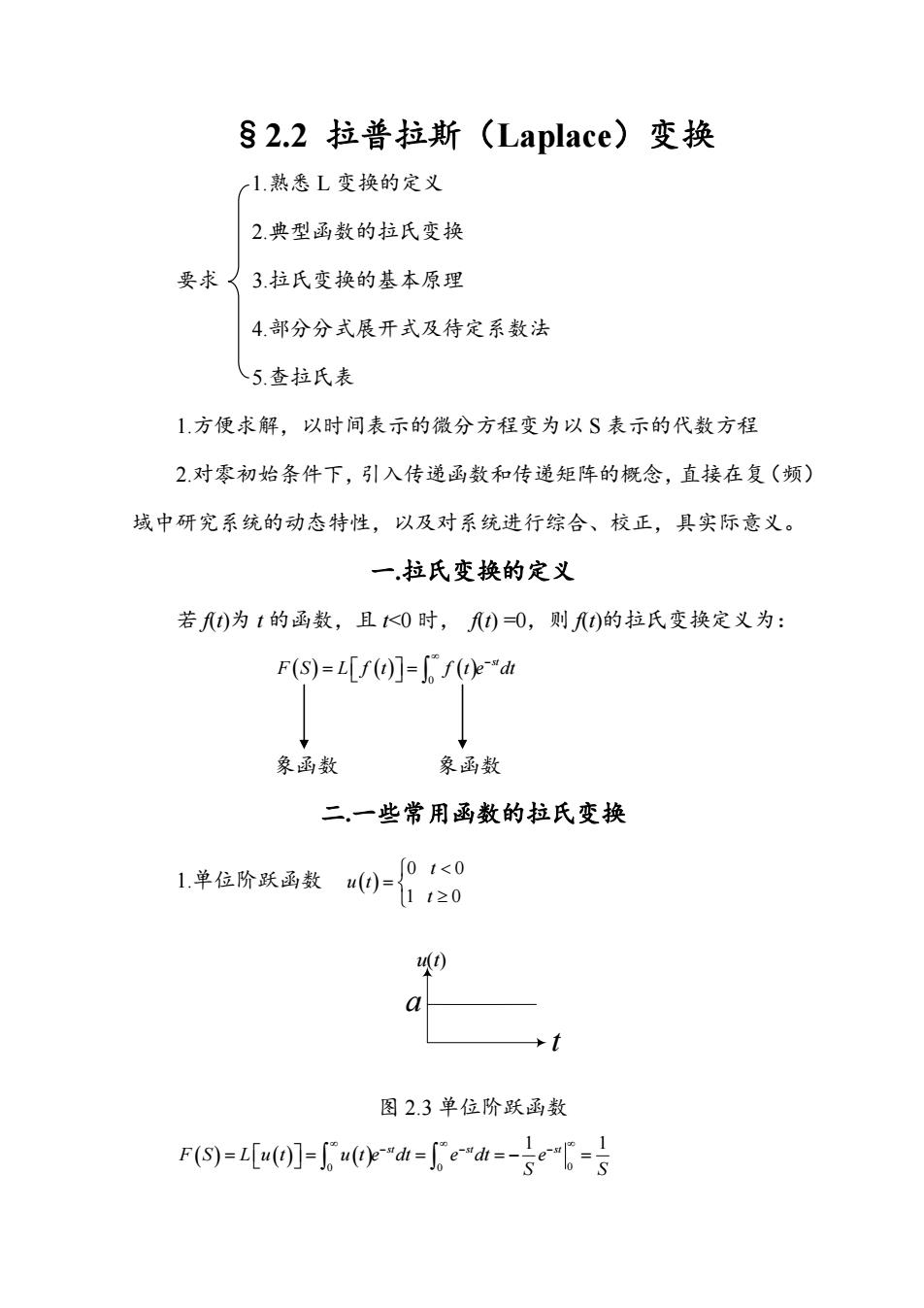
§2.2 拉普拉斯（Laplace）变换 1.熟悉 L 变换的定义 2.典型函数的拉氏变换 要求 3.拉氏变换的基本原理 4.部分分式展开式及待定系数法 5.查拉氏表 1.方便求解，以时间表示的微分方程变为以 S 表示的代数方程 2.对零初始条件下，引入传递函数和传递矩阵的概念，直接在复（频） 域中研究系统的动态特性，以及对系统进行综合、校正，具实际意义。 一.拉氏变换的定义 若 f(t)为 t 的函数，且 t<0 时， f(t) =0，则 f(t)的拉氏变换定义为：       0 st F S L f t f t e dt          象函数 象函数 二.一些常用函数的拉氏变换 1.单位阶跃函数   0 0 1 0 t u t t       u(t) t a 图 2.3 单位阶跃函数       0 0 0 st st st 1 1 F S L u t u t e dt e dt e S S                  

所：用-日 01<0 2.单位脉冲函数60= ©0s1s 04 1/e 图2.4单位脉冲函数 F-401-g片=2号 ]四 所以：6=1 3单位斜放函盘（建度画数）0-日0 ◆0 图2.5单位脉冲函数 F(S)=Lf()]=d=-de" 由∫w=n-∫ahr可知

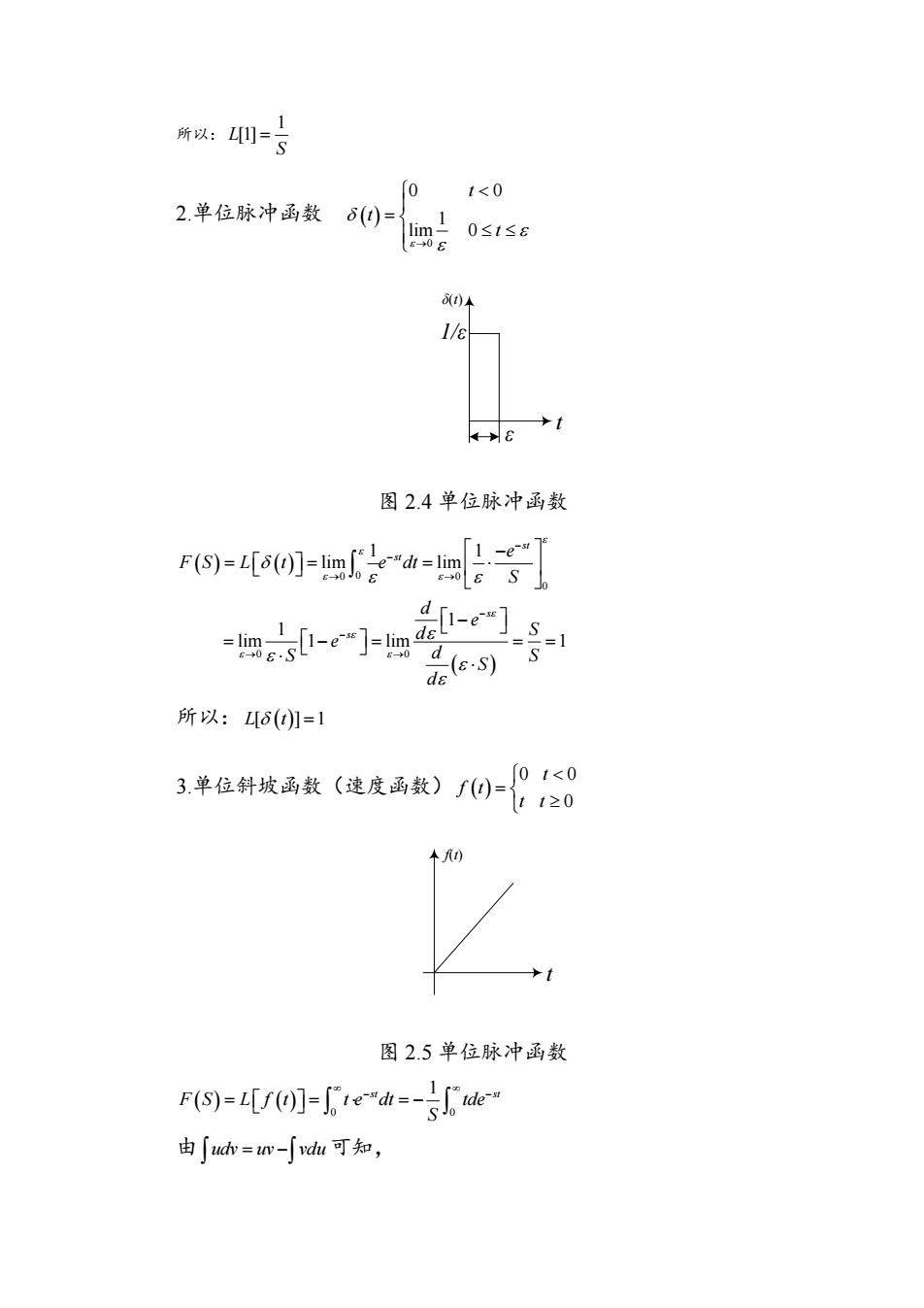
所以： 1 L[1] S  2.单位脉冲函数   0 0 0 1 lim 0 t t t               δ(t) t ε 1/ε 图 2.4 单位脉冲函数       0 0 0 0 0 0 1 1 lim lim 1 1 lim 1 lim 1 st st s s e F S L t e dt S d e d S e S S d S d                                                        所以： L t [ ] 1     3.单位斜坡函数（速度函数）   0 0 0 t f t t t       f(t) t 图 2.5 单位脉冲函数     0 0 st st 1 F S L f t t e dt tde S                由 udv uv vdu     可知