
一、定义 上述2个实例说明系统的稳定反映在干扰消失后的过渡过程 的性质上,因此,控制系统的稳定性可以这样定义: 若控制系统在任何足够小的初始偏差的作用下,其过渡过 程随时间的推移,逐渐衰减至零,具有恢复原平衡状态的性能, 则称该系统稳定。 xo(t) xo(t) x(t) 系统自由振荡输出三种情况 7/88
7/88 上述2个实例说明系统的稳定反映在干扰消失后的过渡过程 的性质上,因此,控制系统的稳定性可以这样定义: 若控制系统在任何足够小的初始偏差的作用下,其过渡过 程随时间的推移,逐渐衰减至零,具有恢复原平衡状态的性能, 则称该系统稳定。 xo(t) xo(t) xo(t) 系统自由振荡输出三种情况 一、定义

即:若线性系统受到扰动的作用而使输出量x()发生偏差, 产生△x,(①)。扰动消失后,经过足够长的时间,该偏差的 绝对值小于给定的正值。 lim△x,(t)≤& 100 则系统稳定,否则不稳定。 近稳定: 1imx,(t)→0 (一般所讲的线性系统的稳定性,就是渐近稳定性) 如果系统在任意初始条件下都保持近稳定,则称为大 范围内渐近稳定。 8/88
即:若线性系统受到扰动的作用而使输出量xo (t)发生偏差, 产生△ xo (t)。扰动消失后,经过足够长的时间,该偏差的 绝对值小于给定的正值ε。 8/88 0 lim ( ) t x t → 则系统稳定,否则不稳定。 0 lim ( ) 0 t x t → 渐近稳定: → (一般所讲的线性系统的稳定性,就是渐近稳定性) 如果系统在任意初始条件下都保持渐近稳定,则称为大 范围内渐近稳定
注意事项: 1.线性系统不稳定现象发生与否,取决于系统内部条件, 而与输入无关。 线性系统的稳定性只取决于系统本身的结构参数,而与 输入无关。(非线性系统的稳定性与输入有关) 2.系统发生不稳定现象必有适当的反馈作用。 X,(s) E(s) Xo(s) G(s) 9/88
注意事项: 1.线性系统不稳定现象发生与否,取决于系统内部条件, 而与输入无关。 线性系统的稳定性只取决于系统本身的结构参数,而与 输入无关。(非线性系统的稳定性与输入有关) 2.系统发生不稳定现象必有适当的反馈作用。 9/88 1 G s( ) ( ) X s i + − 0 X s( ) E s( )

3.控制理论中所讨论的稳定性其实都是指自由振荡下的 稳定性,即:讨论输入为0,系统仅存在有初始状态不为0时 的稳定性,即讨论系统自由振荡是收敛的还是发散的。 I川 讨论系统初始状态为0时,系统脉冲响应是收敛的还是发散的。 至于机械工程系统,往往用激励或加外力的方发施以强 迫振动或运动,因而造成系统共振(或谐振)或偏离平衡位 置越来越远,这不是控制理论所要讨论的稳定性。 10/88
3.控制理论中所讨论的稳定性其实都是指自由振荡下的 稳定性,即:讨论输入为0,系统仅存在有初始状态不为0时 的稳定性,即讨论系统自由振荡是收敛的还是发散的。 至于机械工程系统,往往用激励或加外力的方发施以强 迫振动或运动,因而造成系统共振(或谐振)或偏离平衡位 置越来越远,这不是控制理论所要讨论的稳定性。 10/88 讨论系统初始状态为0时,系统脉冲响应是收敛的还是发散的
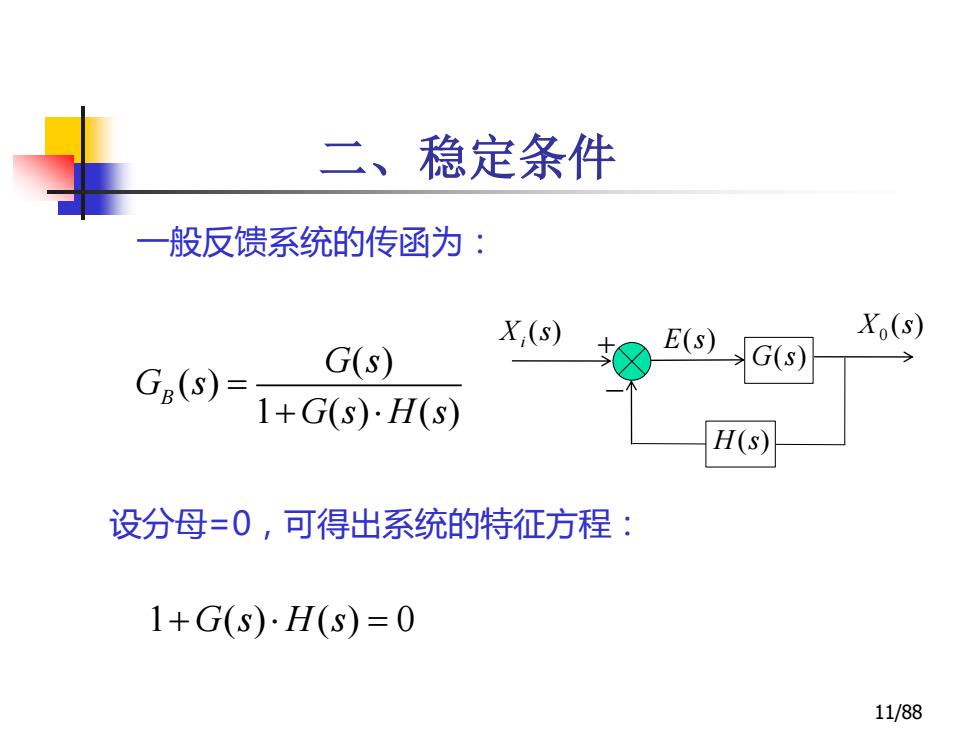
二、稳定条件 一般反馈系统的传函为: X,(s) E(s) Xo(s) G(s) G(S)= G(s) 1+G(s)·H(S) H(s) 设分母=0,可得出系统的特征方程: 1+G(s)H(s)=0 11/88
一般反馈系统的传函为: 11/88 二、稳定条件 G s( ) ( ) X s i + − 0 X s( ) E s( )H s( ) ( ) ( ) 1 ( ) ( ) B G s G s G s H s = + 设分母=0,可得出系统的特征方程: 1 ( ) ( ) 0 + = G s H s