《机械测试技术基础》课程教学资源（作业习题）测试技术习题与答案

机械测试技术基出 习 题 解 答 授课教师：杨文志

机械测试技术基础 习 题 解 答 授课教师：杨文志

第一章习题(P29) 1-1以下信号，个是周期信号？哪个是准周期信号？哪个是既变信号？它们的领谱各其传哪些符征？ (1)cos 2fte (2）sin2xfot+4 sin fot (3)o92xfk+2cos3πf.t 解： (1)瞬变信号一指数衰减振荡信号，其频谱具有连续性和衰减性。 (2)准周期信号，因为各简谐成分的频率比为无理数，其频谱仍具有离散 性。 (3)周期信号，因为各简谐成分的频率比为无理数，其频谱具有离散性、 谐波性和收敛性。 1-2求信号，6e=如2：的有效值（均方根值z-√2(0）： 解：x(t)=sin2:的有效值（均方根值）： VT。 = j0-cs40 1 1 2To dt= (T。一4河 smn4对。) 2T。 4 1 V2T。 sn4河oT。）=1/V2 1-}用傅里叶级数的三角茵数展开式和复指数展开式，求周期三角波（图121）的频谱，并作频谱州 1

1 第一章 习 题（P29） 解： （1）瞬变信号－指数衰减振荡信号，其频谱具有连续性和衰减性。 （2）准周期信号，因为各简谐成分的频率比为无理数，其频谱仍具有离散 性。 （3）周期信号，因为各简谐成分的频率比为无理数，其频谱具有离散性、 谐波性和收敛性。 解：x(t)=sin2 f t  0 的有效值（均方根值）： sin 4 ) 1/ 2 4 1 ( 2 1 sin 4 ) 4 1 ( 2 1 (1 cos 4 ) 2 1 sin 2 1 ( ) 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 0 0 2 0 0 0 0 0 = − = = − = − = =    f T f T T f t f T T f t dt T f t dt T x t dt T x T T T T rms      

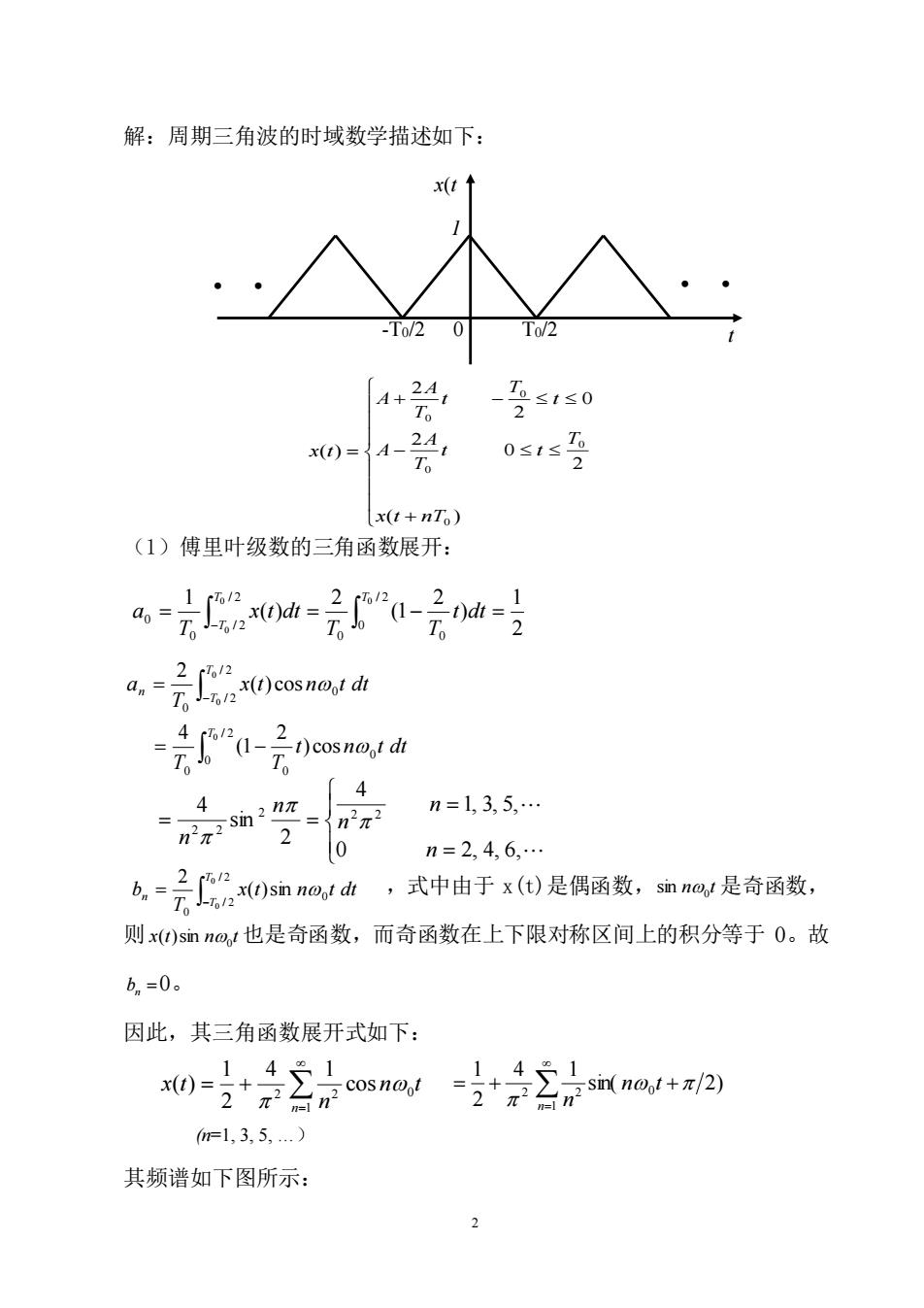
解：周期三角波的时域数学描述如下： x(1 0/20 4+-1≤0 0=4-24, x(t+nT) (1)傅里叶级数的三角函数展开： 2 .(csme T。 「4 京m- 4 n=l,3,5,. = 20 n=2,4,6, 么=号0由@山，式中由于0是偶函数，血@是奇函数。 则x)snn,1也是奇函数，而奇函数在上下限对称区间上的积分等于0。故 b。=0。 因此，其三角函数展开式如下： 1+41 1,41 0=2+产Σosna/2+7Σ7mau+/2 ml,3,5,.) 其频谱如下图所示：

2 解：周期三角波的时域数学描述如下： （1）傅里叶级数的三角函数展开： ，式中由于 x(t)是偶函数， n t 0 sin  是奇函数， 则 x t n t 0 ( )sin  也是奇函数，而奇函数在上下限对称区间上的积分等于 0。故 bn = 0。 因此，其三角函数展开式如下： 其频谱如下图所示： -T0/2 0 T0/2 1 x(t ) t . . . . . .          + −   + −   = ( ) 2 0 2 0 2 2 ( ) 0 0 0 0 0 x t nT T t t T A A t T t T A A x t 2 1 ) 2 (1 2 ( ) 1 / 2 0 0 0 / 2 / 2 0 0 0 0 0 = = − = −  T T T t dt T T x t dt T a   = − = − / 2 0 0 0 0 / 2 / 2 0 0 0 0 0 ) cos 2 (1 4 ( ) cos 2 T T T n t n t dt T T x t n t dt T a        = = = =   0 2, 4, 6, 1, 3, 5, 4 2 sin 4 2 2 2 2 2 n n n n n    − = / 2 / 2 0 0 0 0 ( )sin 2 T T n x t n t dt T b    = = + 1 2 2 0 cos 4 1 2 1 ( ) n n t n x t     = = + + 1 2 2 0 sin( 2) 4 1 2 1 n n t n    (n=1, 3, 5, .）

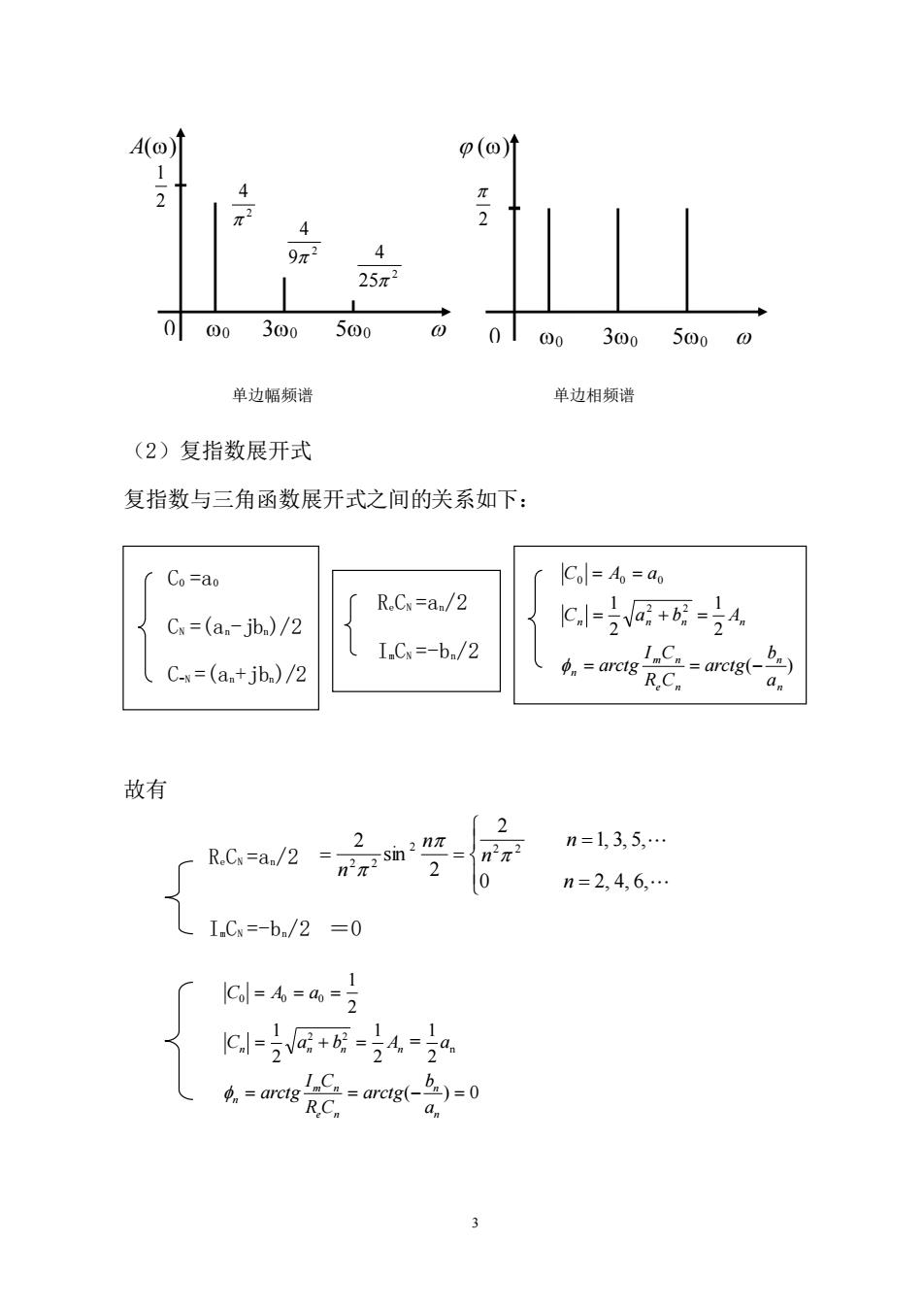
4) p(@) 4 25π 000 300 000 0100300500 单边幅须谱 单边相频谱 (2)复指数展开式 复指数与三角函数展开式之间的关系如下： Co=ao Col=Ao =ao R.Cx=a/2 Cw=(a.-jb.)/2 G园+6-4 I.Cw=-b./2 C-x=(a.+jb.)/2 arct B.C 故有 2 2 =n2π n=13,5,. n=2,4,6,. LI.Cw=-b./2=0 Cd=4=4=2 1 c=)匠+成=4=0 a 3

3 （2）复指数展开式 复指数与三角函数展开式之间的关系如下： 故有 ( ) 0 2 1 = 2 1 2 1 2 1 n 2 2 0 0 0 = = − = = + = = = = n n e n m n n n n n n a b arctg R C I C arctg C a b A a C A a  0  A() 0 30 50 0 0 30 50   () 2 4  2 9 4  2 25 4  2 1 2  C0 =a0 CN =(an-jbn)/2 C-N =(an+jbn)/2 ReCN =an/2 ImCN =-bn/2 ( ) 2 1 2 1 2 2 0 0 0 n n e n m n n n n n n a b arctg R C I C arctg C a b A C A a = = − = + = = =  ReCN =an/2      = = = =   0 2, 4, 6, 1, 3, 5, 2 2 sin 2 2 2 2 2 2 n n n n n    ImCN =-bn/2 ＝0 单边幅频谱 单边相频谱

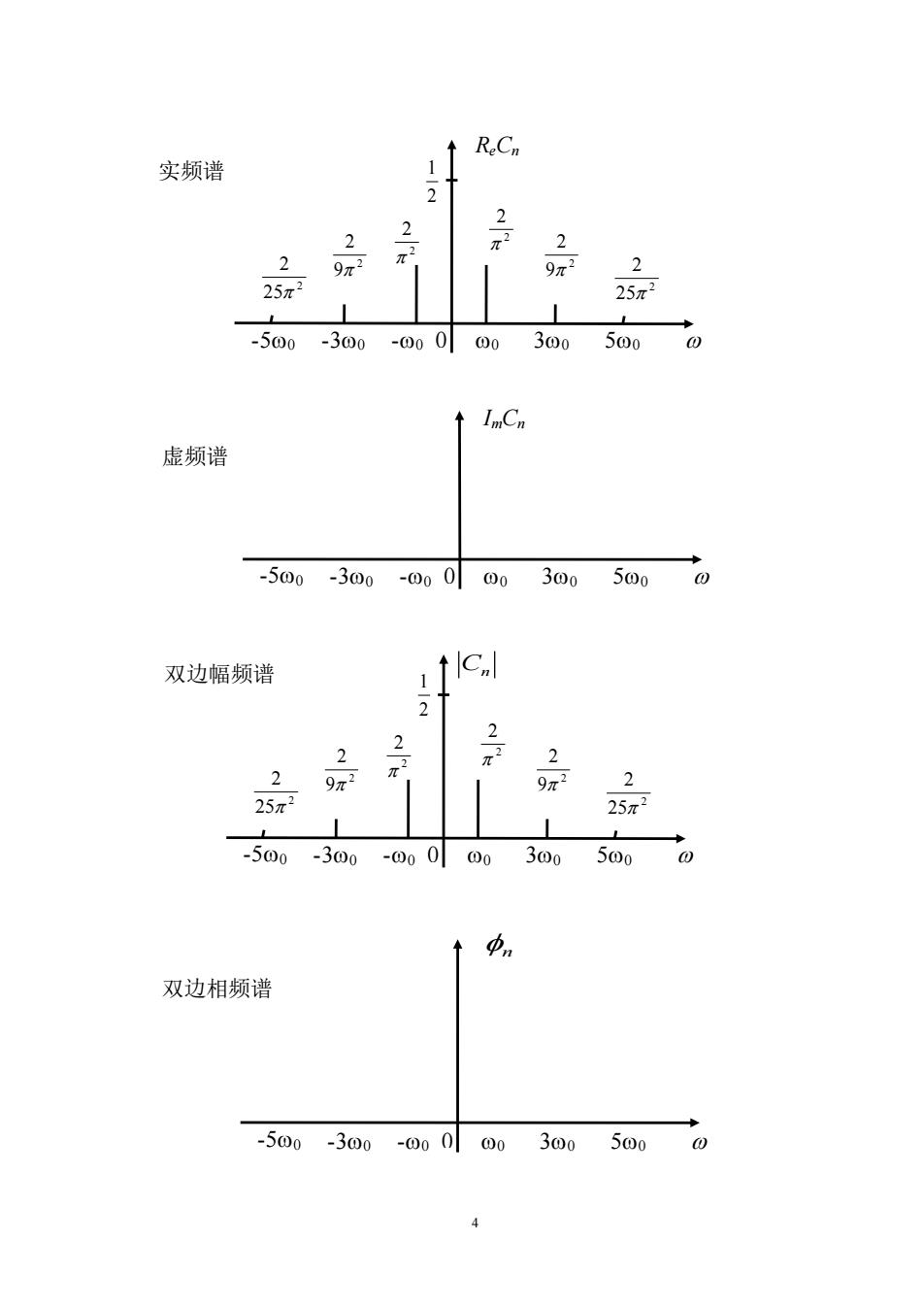
R.Cn 实频谱 2 2 2 2品 2 25r2 -500 -300-00000 300 InCn 虚频谱 -500-300-000003005000 双边幅频谱 2 2 2 2 2 9 25 25m -500-300-000003005000 中n 双边相频谱 -500-300-000003005000

4 0  n -50 -30 -0 0 30 50 0 0 30  2 2  2 1 2 9 2  2 25 2  -30 -0 50 2 9 2  2 25 2  -50 2 2  Cn 0  ImCn -50 -30 -0 0 30 50 0  ReCn 0 30 2 2  2 1 2 9 2  2 25 2  -30 -0 50 2 9 2  2 25 2  -50 2 2  虚频谱 双边相频谱 实频谱 双边幅频谱