《电路》课程教学资源（PPT课件）第6章 一阶电路（电路的过渡过程）

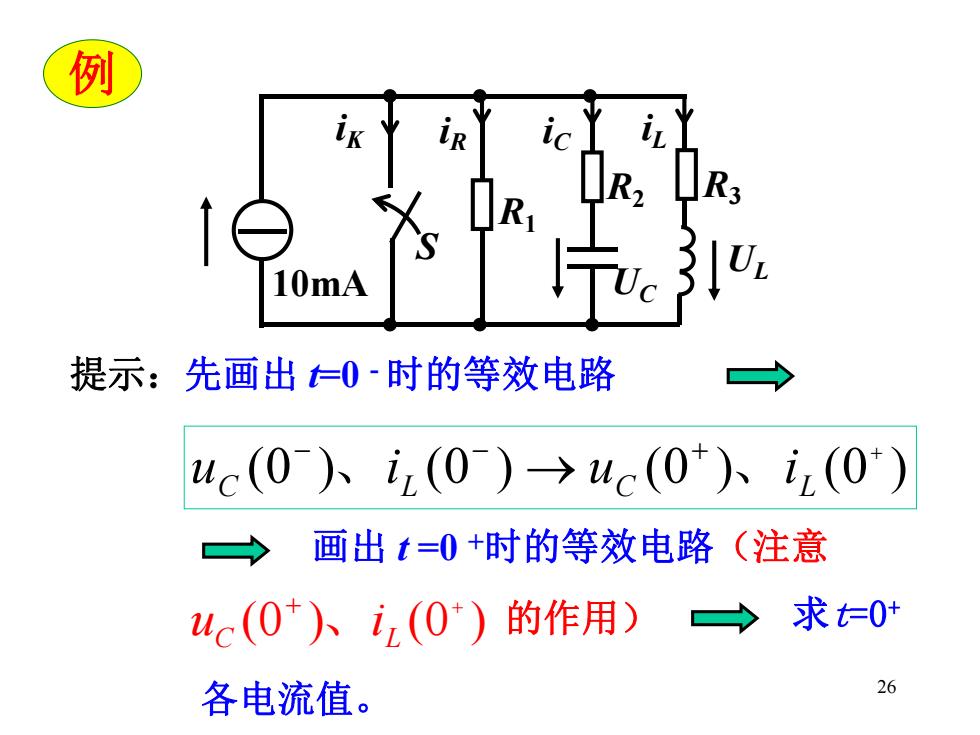
例 10mA 提示：先画出=0时的等效电路 uc(0)人z(0)→uc(0)iz(0) 画出t=0+时的等效电路（注意 uc(0)入iz(0)的作用) 求0 各电流值。 26

26 提示：先画出 t=0 - 时的等效电路 (0 ) (0 ) (0 ) (0 )      C L C L u 、i u 、i 画出 t =0 +时的等效电路（注意 (0 ) (0 )   C L u 、i 的作用） 求t=0 + 各电流值。 10mA iK iR iC iL S R1 R2 R3 UC UL 例

6-2 一阶电路的零输入响应 零输入响应（☑ero-input response):激励（电源）为零，由初 始储能引起的响应。 一阶电路：当电路中只含一个电容或电感时，根据KVL和KCL以 及元件的VCR建立的电路方程是以电容电压或电感电流为变量的 一阶微分方程。 ().一阶电阻电容电路（简称为RC电路)-对于含有一个 电容和一个电阻的电路，当电路的无源元件都是线性和时不变时， 电路方程将是一阶线性常微分方程，相应的电路称为RC电路 (2).一阶电阻电感电路（简称为RL电路)-对于含有一个 电感和一个电阻的电路，当电路的无源元件都是线性和时不变时， 电路方程将是一阶线性常微分方程，相应的电路称为RL电路。 3).一阶动态电路如果电路仅含一个动态元件，则可以把该动 态元件以外的电阻电路用戴维宁定理或诺顿定理置换为电压源和电 阻的串联组合，或电流源和电阻的并联组合，从而把它变换为RC 电路或RL电路

27 (3).一阶动态电路-如果电路仅含一个动态元件，则可以把该动 态元件以外的电阻电路用戴维宁定理或诺顿定理置换为电压源和电 阻的串联组合，或电流源和电阻的并联组合，从而把它变换为R C 电路或R L电路。 一阶电路:当电路中只含一个电容或电感时，根据KVL和KCL以 及元件的VCR建立的电路方程是以电容电压或电感电流为变量的 一阶微分方程。 (1).一阶电阻电容电路（简称为 R C电路）-对于含有一个 电容和一个电阻的电路，当电路的无源元件都是线性和时不变时， 电路方程将是一阶线性常微分方程，相应的电路称为R C电路 (2).一阶电阻电感电路（简称为 RL电路）- 对于含有一个 电感和一个电阻的电路，当电路的无源元件都是线性和时不变时， 电路方程将是一阶线性常微分方程，相应的电路称为RL电路。 6-2 一阶电路的零输入响应 零输入响应(Zeroinput response )：激励(电源)为零，由初 始储能引起的响应

米暂态过程按能量来源可分以下三种响应： 1.零输入响应： 在零输入的条件下，由其内部储能引起的响 应，为零输入响应；此时，u(0+)或i(0) 被视为一种输入信号。 2.零状态响应： 在零状态的条件下即无内部储能，仅由外加 电源激励信号产生的响应为零状态响应。 3.全响应： 电容（电感)上的内部储能和外加电源激励均 不为零时的响应，为全响应。 求解 1。经典法：用数学方法求解微分方程； 方法： 2。三要素法：求初始值，稳态值，时间常数

28 2. 零状态响应： 在零状态的条件下即无内部储能，仅由外加 电源激励信号产生的响应为零状态响应。 3. 全响应： 电容（电感）上的内部储能和外加电源激励均 不为零时的响应，为全响应。 1. 零输入响应： 在零输入的条件下，由其内部储能引起的响 应，为零输入响应； 此时， 被视为一种输入信号。 (0 )  uc (0 )  L 或 i  暂态过程按能量来源可分以下三种响应： 2。三要素法:求初始值，稳态值，时间常数。 求解 1。经典法: 用数学方法求解微分方程； 方法：

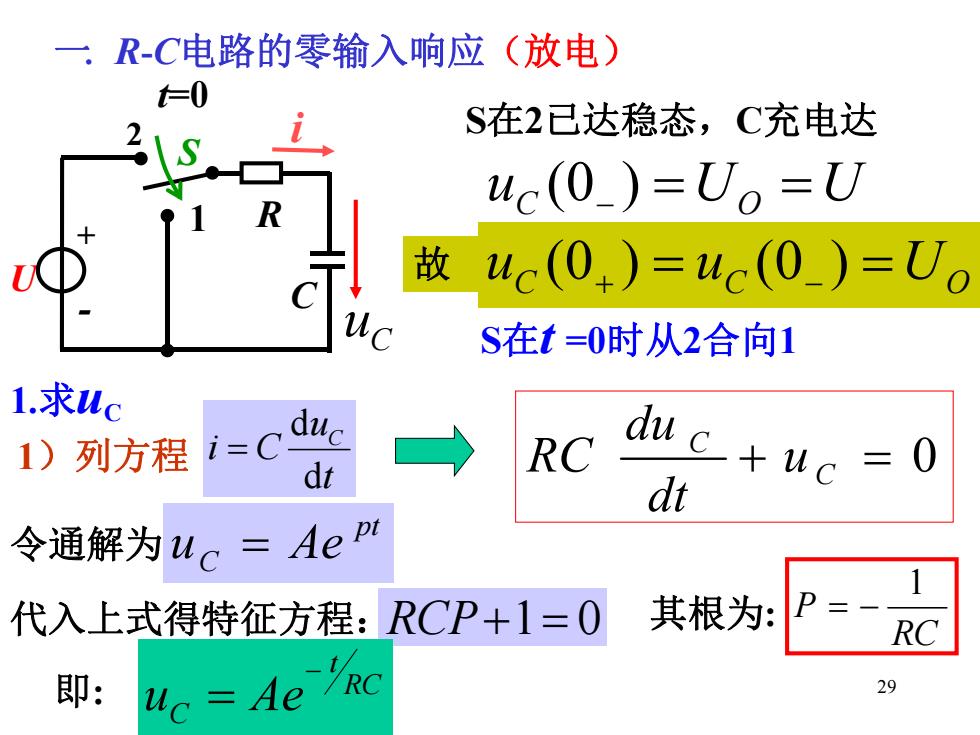
一.R-C电路的零输入响应（放电） =0 S在2已达稳态，C充电达 uc(0)=Uo=U 故uc(0)=uc(0_)=U。 S在t=0时从2合向1 1.求uc 1)列方程 iscd4 dt RC duc+uc :0 dt 令通解为uc= Ae p 1 代入上式得特征方程：RCP+1=0 其根为： RC 即： uc Ae Rc 29

29 2 U + - S 1 R t=0 C uC 一. R-C电路的零输入响应（放电） S在2已达稳态，C充电达 uC (0 ) UO U 故 uC   uC  UO (0 ) (0 ) 1.求uC   0 C C u dt du RC S在t =0时从2合向1 1）列方程 令通解为 pt uC  Ae 代入上式得特征方程：RCP1 0 RC P 1 其根为:   i t u i C C d d  即: RC t uC Ae  

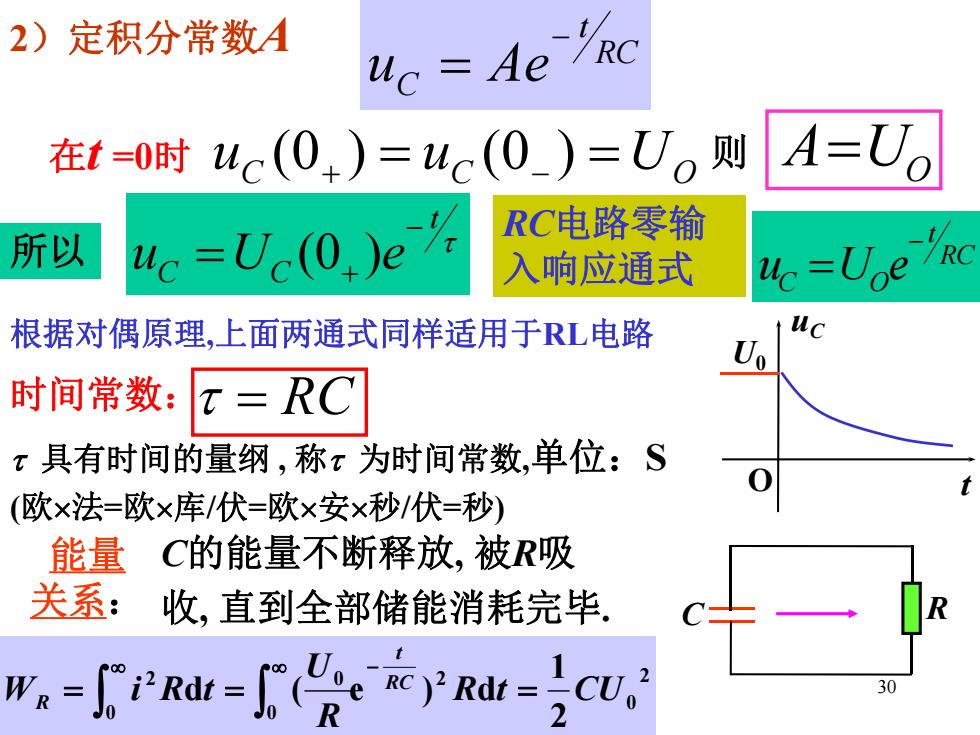
2)定积分常数A uc Ae Rc 在t-0时uc(0,)=uc(0_)=U。则 A=Uo RC电路零输 所以 uc=Uc(0.)e 入响应通式 uc =Uoe R 根据对偶原理，上面两通式同样适用于RL电路 U 时间常数： t=RC x具有时间的量纲，称x为时间常数，单位：S (欧×法=欧×库/伏=欧×安×秒/伏=秒) 能量 C的能量不断释放，被R吸 关系： 收，直到全部储能消耗完毕. wn=Rd=(

30 2）定积分常数A 在t =0时 uC   uC  UO (0 ) (0 ) 则 AUO RC t uC Ae   时间常数：  RC  具有时间的量纲 , 称 为时间常数,单位：S (欧法=欧库/伏=欧安秒/伏=秒) U0 t uC O C的能量不断释放, 被R吸 收, 直到全部储能消耗完毕. 能量 关系： 2 0 2 0 0 0 2 2 1 d ( e ) Rdt CU R U W i R t RC t R         C R RC t C O u U e  所以   t C C u U e    (0 ) RC电路零输 入响应通式 根据对偶原理,上面两通式同样适用于RL电路