四、分析方法 经典法 时域分析法 拉普拉斯变换法 频域分析法 状态变量法 时域分析法 解析法 数值法 +RC dr2 duc+uc=Us dt (0) 动态电路的阶数: 一阶电路:一阶微分方程所描述的电路」 二阶电路:二阶微分方程所描述的电路。 高阶电路:高阶微分方程所描述的电路. 6
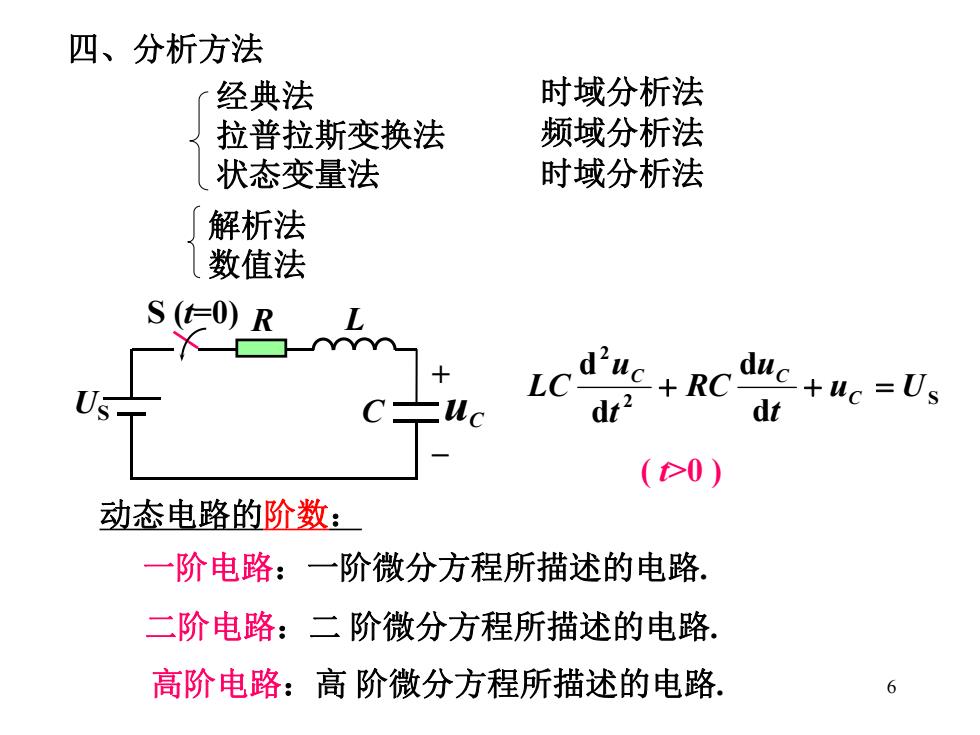
6 四、分析方法 2 S 2 d d d d u U t u RC t u LC C C C 一阶电路:一阶微分方程所描述的电路. 二阶电路:二 阶微分方程所描述的电路. S (t=0) L US C + –uC R ( t>0 ) 经典法 拉普拉斯变换法 状态变量法 时域分析法 频域分析法 时域分析法 解析法 数值法 动态电路的阶数: 高阶电路:高 阶微分方程所描述的电路
产生过渡过程的电路及原因? 一.电阻电路 t=0 R 无暂态过程 电阻是耗能元件,其上电流随电压成比例变化, 不存在暂态过程
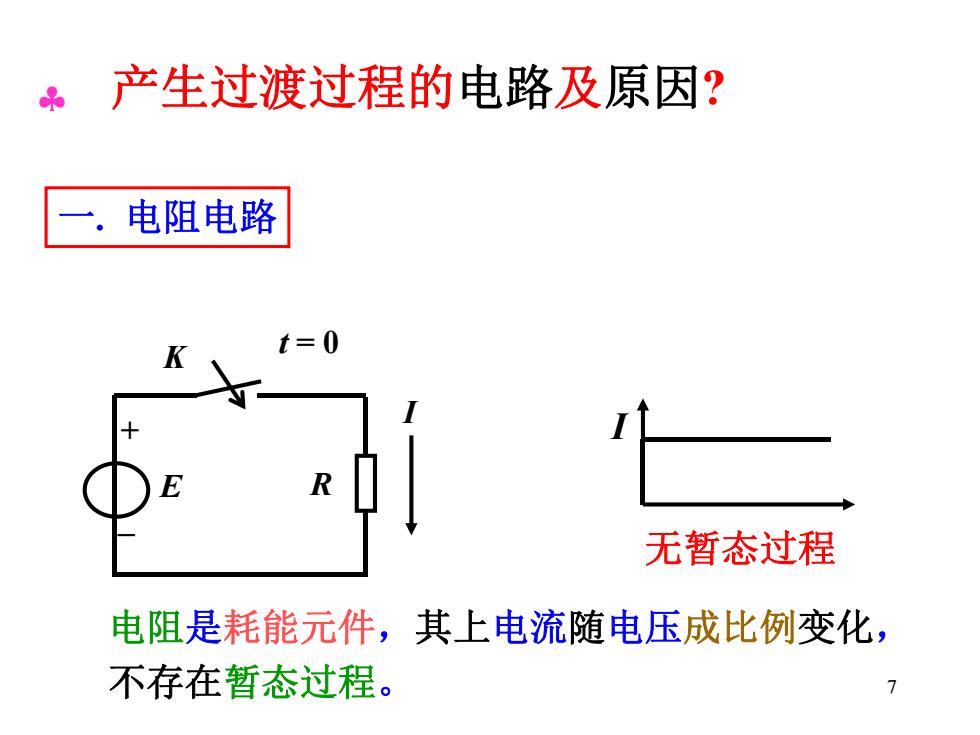
7 无暂态过程 I 一. 电阻电路 t = 0 E R + _ I K 电阻是耗能元件,其上电流随电压成比例变化, 不存在暂态过程。 产生过渡过程的电路及原因?
二,电容电路 储能元件 lc= dt 电容元件的电压和电流的约束关系是通过导数(或积分 )表达的,所以称为储能元件(动态元件)。它储存的 能量为电场能量,其大小为: c=边= -cuc 因为能量的存储和释放需要一个过程,所以有电 容的电路存在暂态过程。即 uc不能突变
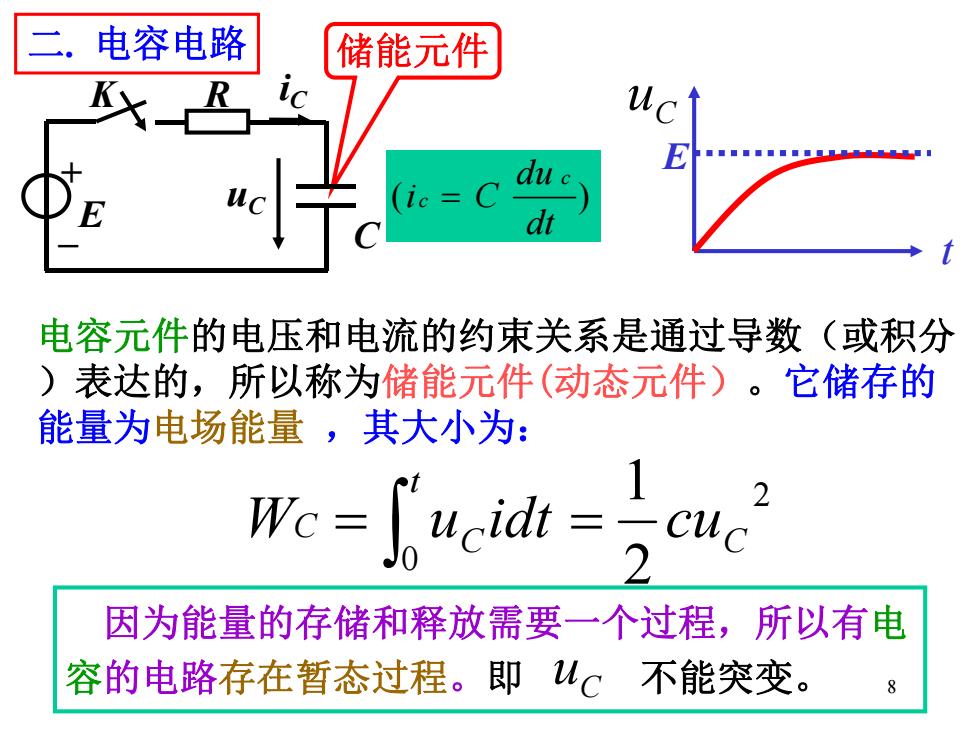
8 E t C u 2 0 2 1 C t C WC u idt cu 储能元件 C 因为能量的存储和释放需要一个过程,所以有电 容的电路存在暂态过程。即 u C 不能突变。 电容元件的电压和电流的约束关系是通过导数(或积分 )表达的,所以称为储能元件(动态元件)。它储存的 能量为电场能量 ,其大小为: ( ) dt du i C c c 二. 电容电路 E K R + _ uC iC

三。电感电路 储能元件 dt 电感元件的电压和电流的约束关系是通过导数(或 积分)表达的,所以称为储能元件(动态元件),它储 存的能量为磁场能量,其大小为: WL- ,h=24 因为能量的存储和释放需要一个过程,所以有电 感的电路存在暂态过程。即1,不能突变
9 t L i 储能元件 电感元件的电压和电流的约束关系是通过导数(或 积分)表达的,所以称为储能元件(动态元件) ,它储 存的能量为磁场能量,其大小为: 2 0 2 1 L L t W L ui dt Li 因为能量的存储和释放需要一个过程,所以有电 感的电路存在暂态过程。即 i L 不能突变。 ( ) dt di u C l l 三. 电感电路 K R E + _ t=0 iL + _ uL

结论 说明 有储能元件(L、C) 的电路 直流电路、交流 电路都存在暂态 在换路时存在暂态过程; 过程,本章只分 没有储能作用的电阻(R) 析讨论直流电路 电路,不存在暂态过程。 的暂态过程。 研究暂态过程的意义:暂态过程是一种自然现象, 对它的研究很重要。暂态过程的存在有利有弊。有 利的方面,如电子技术中常用它来产生各种波形; 不利的方面,如在暂态过程发生的瞬间,可能出现 过压或过流,致使设备损坏,必须采取防范措施。10
10 有储能元件(L、C)的电路 在换路时存在暂态过程; 没有储能作用的电阻(R) 电路,不存在暂态过程。 直流电路、交流 电路都存在暂态 过程,本章只分 析讨论直流电路 的暂态过程。 研究暂态过程的意义:暂态过程是一种自然现象, 对它的研究很重要。暂态过程的存在有利有弊。有 利的方面,如电子技术中常用它来产生各种波形; 不利的方面,如在暂态过程发生的瞬间,可能出现 过压或过流,致使设备损坏,必须采取防范措施。 结 论 说 明