
核心重难探究 知识点一:二次函数y=x-h)2+k的图象与性质 【例1】已知函数,2+22+2和2+22-3. (1)在同一个平面直角坐标系中画出这三个函数的图象; (2)分别说出这三个函数图象的开口方向、对称轴和顶点坐 标; (3)试讨论函数y=(c-2)2+3的性质. 导航页
导航页 核心重难探究 知识点一:二次函数y=a(x-h) 2+k的图象与性质 【例 1】 已知函数 y= 𝟏 𝟐 x 2 ,y= 𝟏 𝟐 (x+2)2 +2 和 y= 𝟏 𝟐 (x+2)2 -3. (1)在同一个平面直角坐标系中画出这三个函数的图象; (2)分别说出这三个函数图象的开口方向、对称轴和顶点坐 标; (3)试讨论函数y= (x-2)2+3的性质. 𝟏 𝟐
核心重难探究 思路点拨:1)建立 ,根据二次函数图象的作法画 出图象即可;2)分别由 可得出开口方向、对称轴 及顶点坐标;3)可以从开口方向、对称轴、顶,点坐标及 方面来谈 导航页
导航页 核心重难探究 思路点拨:(1)建立 ,根据二次函数图象的作法画 出图象即可;(2)分别由 可得出开口方向、对称轴 及顶点坐标;(3)可以从开口方向、对称轴、顶点坐标及 方面来谈
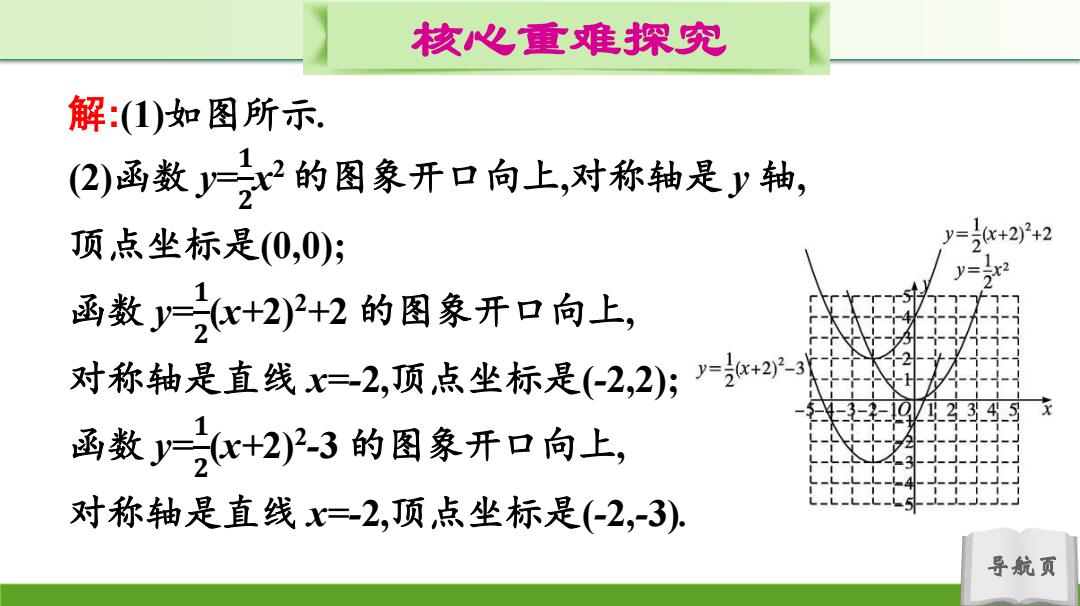
核心重难探究 解:1)如图所示. (2)函数x2的图象开口向上,对称轴是y轴, 顶点坐标是(0,0); y=+2)2+2 函数y=之+2)2+2的图象开口向上, 对称轴是直线x=-2,顶点坐标是(-2,2); =+22-3 函数2+2)3的图象开口向上, 对称轴是直线x=2,顶点坐标是(-2,-3), 导航页
导航页 核心重难探究 解:(1)如图所示. (2)函数 y= 𝟏 𝟐 x 2 的图象开口向上,对称轴是 y 轴, 顶点坐标是(0,0); 函数 y= 𝟏 𝟐 (x+2)2 +2 的图象开口向上, 对称轴是直线 x=-2,顶点坐标是(-2,2); 函数 y= 𝟏 𝟐 (x+2)2 -3 的图象开口向上, 对称轴是直线 x=-2,顶点坐标是(-2,-3)

核心重难探究 (3)函数yc-2)2+3的性质: ①图象的开口方向向上; ②图象的对称轴为x=2; ③图象的顶点坐标为(2,3); ④当x>2时,函数y的值随x的增大而增大;当x<2时,函数y的值 随x的增大而减小;当x=2时,函数y取得最小值3. 【方法归纳】 解决这类问题先要正确作出二次函数的图象,再利用数形结 合思想求解其他问题即可. 导航页
导航页 核心重难探究 【方法归纳】 解决这类问题先要正确作出二次函数的图象,再利用数形结 合思想求解其他问题即可. (3)函数 y= 𝟏 𝟐 (x-2)2 +3 的性质: ①图象的开口方向向上; ②图象的对称轴为x=2; ③图象的顶点坐标为(2,3); ④当x>2时,函数y的值随x的增大而增大;当x<2时,函数y的值 随x的增大而减小;当x=2时,函数y取得最小值3