
第4章动量和角动量 §4.1动量定理动量守恒定律 §4.2质心质心运动定理 §4.3碰撞问题 §4.4火箭飞行基本原理 §4.5质点的角动量角动量守恒定律 §4.6质点系的角动量
第 4 章 动量和角动量 §4.1 动量定理 动量守恒定律 §4.2 质心 质心运动定理 §4.3 碰撞问题 §4.5 质点的角动量 角动量守恒定律 §4.4 火箭飞行基本原理 §4.6 质点系的角动量
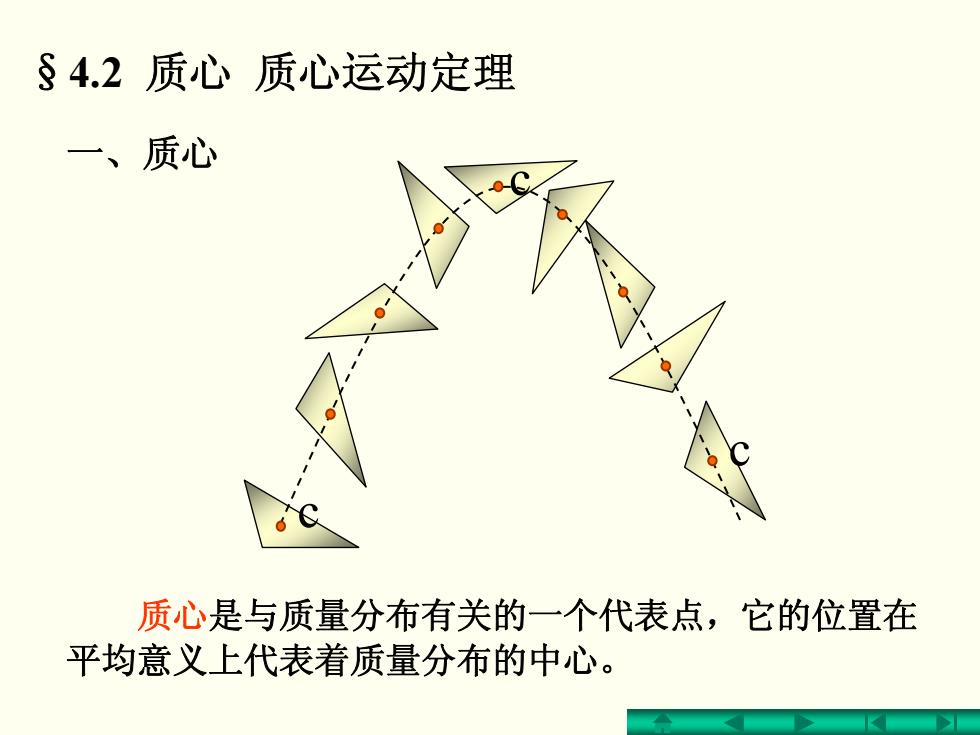
§4.2质心质心运动定理 一、质心 质心是与质量分布有关的一个代表点,它的位置在 平均意义上代表着质量分布的中心
§4.2 质心 质心运动定理 一、质心 质心是与质量分布有关的一个代表点,它的位置在 平均意义上代表着质量分布的中心。 c c c
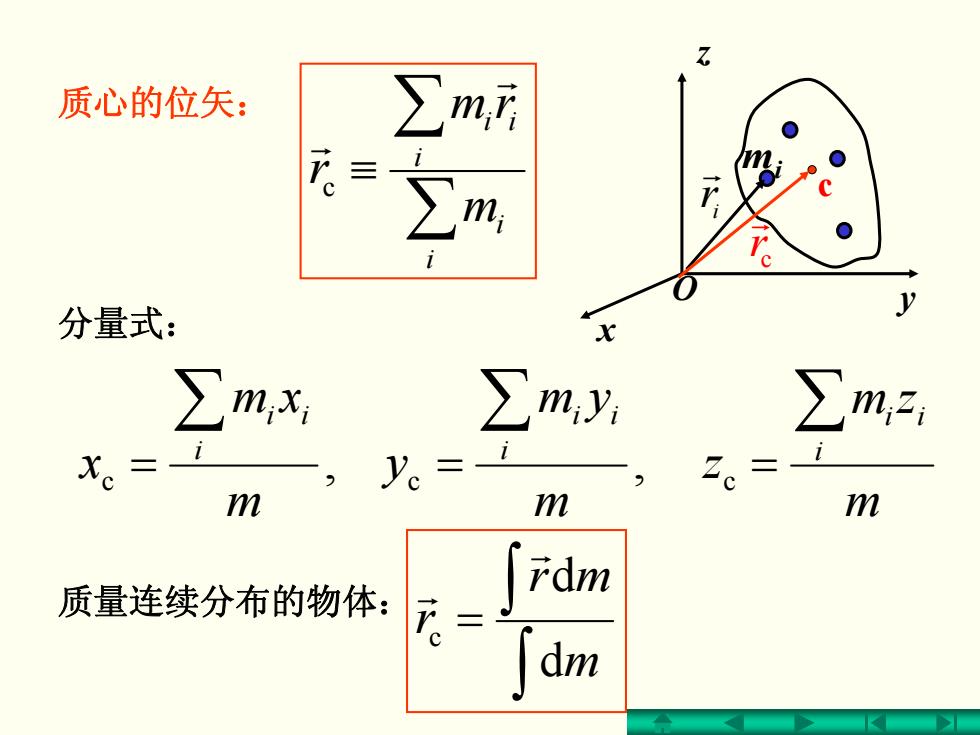
质心的位矢: ∑m,d 三 ∑ i 分量式: ∑m,x ∑m,y ∑m, 。= y。= 2。= m m m rdm 质量连续分布的物体: 元。= dm
质心的位矢: ∑ ∑ ≡ i i i ii m rm r r r c , c m xm x i ∑ ii = 分量式: ∫ ∫ = m mr r d d c r r , c m ym y i ∑ ii = m zm z i ∑ ii c = 质量连续分布的物体: x y z ir r mi cr r O c

rdm 分量式: 「dm ∫xdm ∫dm 质量线分布:dm=p,dl 质量面分布: dm=pds 质量体分布:dm=pdV
∫ ∫ = m mx x d d c 分量式: = ρ sdd sm = ρ dd Vm 质量线分布: 质量面分布: 质量体分布: ∫ ∫ = m mr r d d c r r ∫ ∫ = m my y d d c ∫ ∫ = m mz z d d c = ρ ldd lm

[例4-5求半圆环的质心。 解:dm=P,dl=P,Rd0 x。=∫xdn/m =jxp,Rd/元Rp, -@l0=2R 元 >质心不一定位于物体内部
[例4-5] 求半圆环的质心。 = ∫ l d πRRx ρθρ l mmxx ∫ = d c ∫ = π 0 dsin π 1 R θθ ¾ 质心不一定位于物体内部。 解: θ R x y O dl c π 2R = = ρ = ρll Rlm ddd θ