
第6章振动力学基础
第 6 章 振动力学基础

第6章振动力学基出 §6.1简谐振动动力学 §6.2简谐振动运动学 §6.3微振动的简谐近似 §6.4平行简谐振动的合成振动频谱 §6.5垂直简谐振动的合成 §6.6阻尼振动 §6.7受迫振动共振
第 6 章 振动力学基础 §6.1 简谐振动动力学 §6.2 简谐振动运动学 §6.3 微振动的简谐近似 §6.5 垂直简谐振动的合成 §6.4 平行简谐振动的合成 振动频谱 §6.6 阻尼振动 §6.7 受迫振动 共振

振动是一种普遍存在的运动形式: 物体的来回往复运动(弹簧振子、钟摆等) 电流、电压的周期性变化 机械振动:物体在一定位置附近作来回往复的运动 可以证明任何复杂的振动都可以认为是由若干个 简单的基本振动合成的。这种简单而又基本的振动形 式称为简谐振动
振动是一种普遍存在的运动形式: 物体的来回往复运动(弹簧振子、钟摆等) 电流、电压的周期性变化 机械振动: 物体在一定位置附近作来回往复的运动 可以证明任何复杂的振动都可以认为是由若干个 简单的基本振动合成的。这种简单而又基本的振动形 式称为简谐振动

§61简谐振动动力学 简谐振动:凡质点的运动遵从余弦(或正弦) 规律时,其运动形式为简谐振动。 x=Acos(@t+o)
简谐振动:凡质点的运动遵从余弦(或正弦) 规律时,其运动形式为简谐振动。 = ω tAx +ϕ )cos( §6.1 简谐振动动力学 t x o
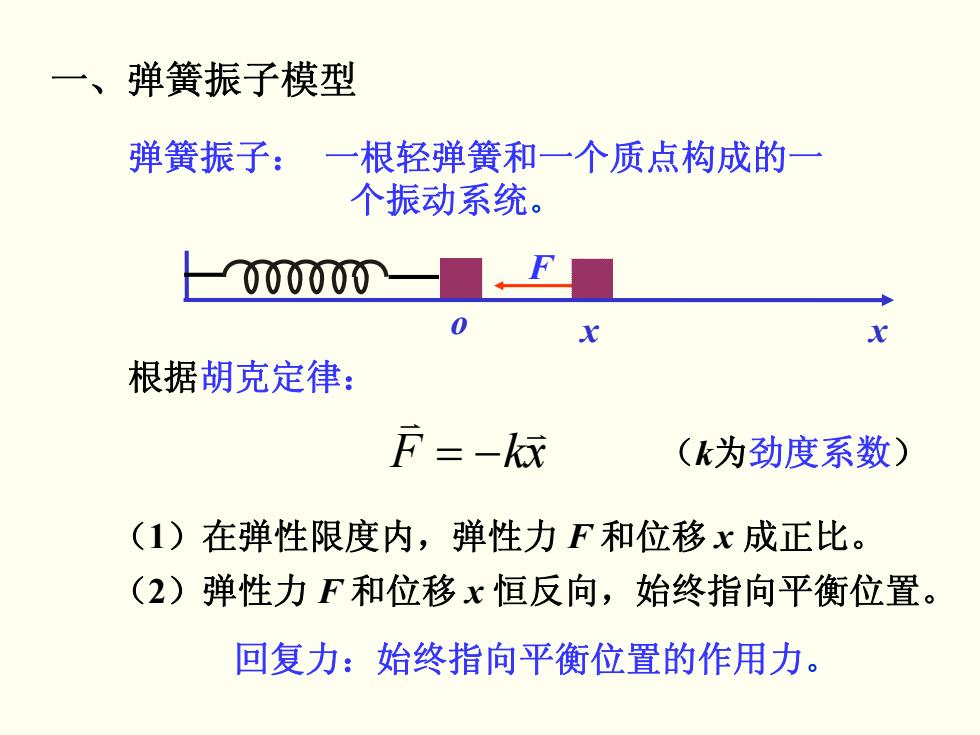
一、弹簧振子模型 弹簧振子:一根轻弹簧和一个质点构成的一 个振动系统。 000000 0 根据胡克定律: F=- (k为劲度系数) 1)在弹性限度内,弹性力F和位移x成正比。 (2)弹性力F和位移x恒反向,始终指向平衡位置。 回复力:始终指向平衡位置的作用力
一、弹簧振子模型 弹簧振子: 一根轻弹簧和一个质点构成的一 个振动系统 。 F 根据胡克定律: xkF ( k 为劲度系数 ) v v −= ( 1)在弹性限度内,弹性力 F 和位移 x 成正比。 ( 2)弹性力 F 和位移 x 恒反向,始终指向平衡位置。 回复力:始终指向平衡位置的作用力 。 o x x