
第5章刚体力学基出 §5.1刚体运动的描述 §5.2刚体的定轴转动定理 §5.3刚体的转动惯量 §5.4刚体定轴转动的角动量守恒定律 §5.5刚体定轴转动的功能原理 §5.6回转仪进动 §5.7刚体的平面运动
第 5 章 刚体力学基础 §5.1 刚体运动的描述 §5.2 刚体的定轴转动定理 §5.3 刚体的转动惯量 §5.4 刚体定轴转动的角动量守恒定律 §5.5 刚体定轴转动的功能原理 §5.6 回转仪 进动 §5.7 刚体的平面运动

§5.3刚体的转动惯量 一、刚体的转动惯量及其计算 定义: J=∑Am,r 单位(SI):kgm2 1.刚体由分立的质点组成时:J=∑m, 2.刚体为质量连续体时: J=∫r2dm >转动惯量仅取决于刚体本身的性质,即与刚体的形 状、大小、质量分布以及转轴的位置有关
定义: ∑Δ≡ i iirmJ 2 1. 刚体由分立的质点组成时: = ∑ i iirmJ 2 ∫ = dmrJ 2 2. 刚体为质量连续体时: 单位( SI ): 2 ⋅mkg ¾ 转动惯量仅取决于刚体本身的性质,即与刚体的形 状、大小、质量分布以及转轴的位置有关。 一、刚体的转动惯量及其计算 §5.3 刚体的转动惯量

[例5-4求均质细棒(m,)的转动惯量: ()转轴通过中心与棒垂直, J=Jridm (2)转轴通过棒的一端与棒垂直。 m 解:(1)dm=- m dx dm J=∫x2dm dx dx= -ml2 1 dm 2J=「 dx >可见,转动惯量因转轴位置而变,故必须指明 是关于某轴的转动惯量
[ 例5-4] 求均质细棒( m , l ) 的转动惯量: (1) 转轴通过中心与棒垂直, (2) 转轴通过棒的一端与棒垂直。 解: x l m m = dd ∫ = dmxJ 2 2 2 12 1 d 2 2 mlxx l l m l = = ∫− ∫ = = l mlxx l m J 0 2 2 3 1 d (1) ∫ = dmrJ 2 (2) ¾ 可见,转动惯量因转轴位置而变,故必须指明 是关于某轴的转动惯量 。 O x O dx x d m dx d m
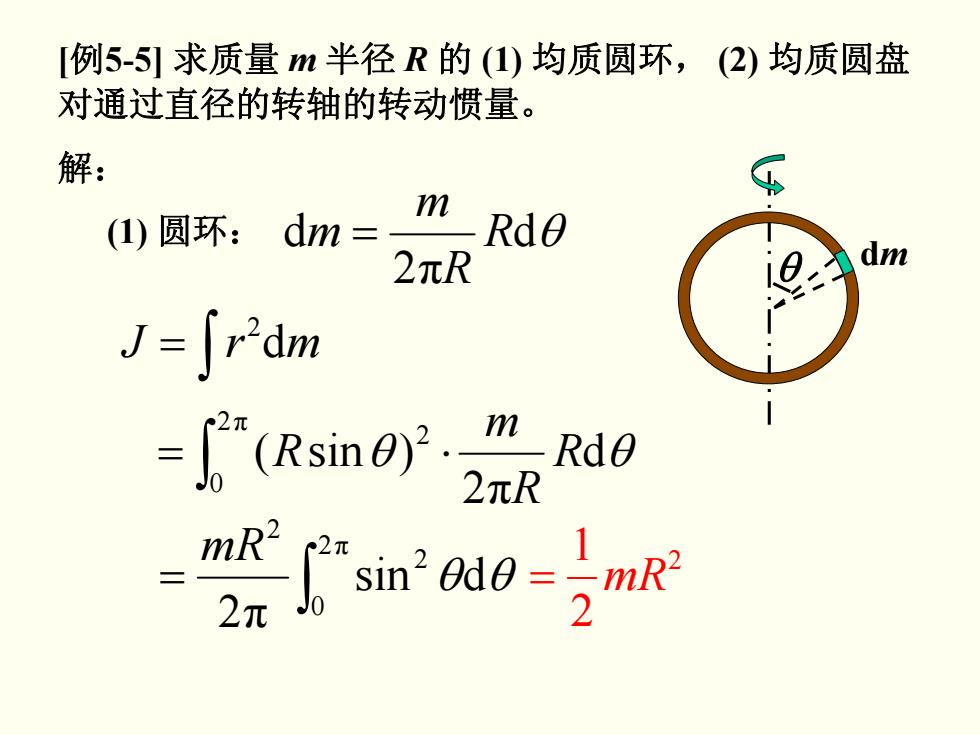
[例5-5求质量m半径R的(1)均质圆环,(2)均质圆盘 对通过直径的转轴的转动惯量。 解: m ()圆环:dm= Rd0 2元R dm J=∫rdm "(Rsin)m Rde 2元R mR- 2元 2 sin20de=mR2 2
[例5-5] 求质量 m 半径 R 的 (1) 均质圆环, (2) 均质圆盘 对通过直径的转轴的转动惯量。 解: dθ 2π d R R m m = ∫ = dmrJ 2 ∫ = ⋅ 2π 0 2 d 2π θ )sin( R θ Rm R 2 2 1 = mR (1) 圆环: dsin θθ 2π 2π 0 2 2 ∫ = mR θ dm

(2)圆盘:dm= 02p J-SdJ-JSpidm dm 1 mR2 >可见,转动惯量与刚体的质量分布有关
2 4 1 = mR o ρ dm (2) 圆盘: 2π dρρ π d 2 Rm m = ∫∫ JJ == dm 21 d 2 ρ ¾ 可见,转动惯量与刚体的质量分布有关。 ∫ = R Rm 0 2 2 2π d 2 π 1 ρρρ