
第22章量子力学基础 §22.1实物粒子的波动性 §22.2波函数及统计解释 §22.3不确定性关系 §22.4薛定谔方程 §22.5力学量算符的本征值问题 §22.6薛定谔方程的应用 §22.7氢原子量子理论 §22.8电子的自旋泡利不相容原理
§22.1 实物粒子的波动性 §22.2 波函数及统计解释 §22.3 不确定性关系 §22.4 薛定谔方程 §22.6 薛定谔方程的应用 §22.5 力学量算符的本征值问题 §22.7 氢原子量子理论 §22.8 电子的自旋 泡利不相容原理 第 22 章 量子力学基础
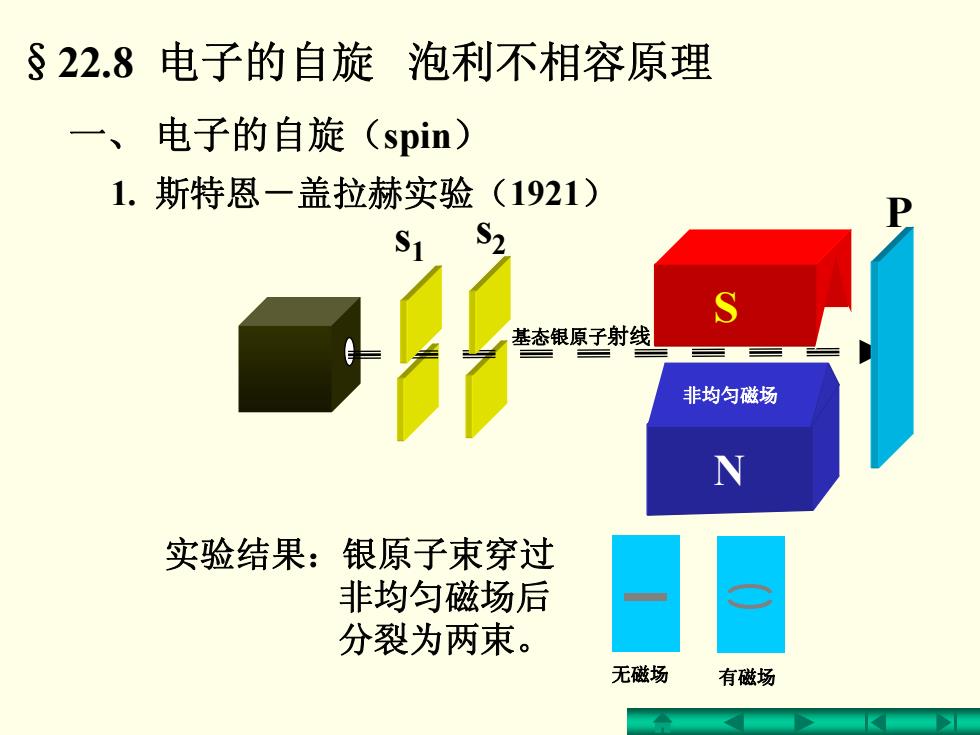
§22.8电子的自旋 泡利不相容原理 一、 电子的自旋(spin) 1.斯特恩一盖拉赫实验(1921) S1 S2 基态银原子射线 非均匀磁场 N 实验结果:银原子束穿过 非均匀磁场后 分裂为两束。 无磁场 有磁场
§22.8 电子的自旋 泡利不相容原理 一、 电子的自旋(spin) 无磁场 有磁场 1. 斯特恩-盖拉赫实验(1921) 实验结果:银原子束穿过 非均匀磁场后 分裂为两束。 s1 s2 P 基态银原子射线 N S 非均匀磁场

实验出现了新的矛盾: 实验用的银原子大部分处在基态(1=0),无磁 矩,银原子不应该受到磁力的偏转。 但按电磁学知,一磁偶极子在非均匀磁场中,除了 受力矩的作用,还受力的作用,且有 OB. F=4 Oz 其中4,为磁偶极子的磁矩,B/a为外磁场沿z方 向的梯度,F,为沿方向受的磁力。 ·但实验结果说明银原子有磁矩,而且沿外磁场方向 有两个分量(银原子分裂为两束)。 对应的“轨道”角动量在外磁场方向上的分量取21 +1=2种
但按电磁学知,一磁偶极子在非均匀磁场中,除了 受力矩的作用,还受 力的作用,且有 z B F z zz ∂ ∂ = μ 其中 μ z为磁偶极子的磁矩, ∂B z/ ∂z 为外磁场沿 z 方 向的梯度, Fz为沿 z方向受的磁力。 • 但实验结果说明银原子有磁矩,而且沿外磁场方向 有两个分量(银原子分裂为两束)。 实验出现了新的矛盾: • 实验用的银原子大部分处在基态( l = 0) ,无磁 矩,银原子不应该受到磁力的偏转。 对应的 “轨道 ”角动量在外磁场方向上的分量取 2l +1=2种

2.电子自旋 1925年,乌伦贝克和哥德斯密特(当时他俩还是 研究生)在分析上述实验的基础上假设: 电子除了“轨道”运动还有一种内禀的运动,称为 自旋。相应地有自旋角动量S和自旋磁矩4。 若自旋“轨道量子数”取S= 心称为自旋量子数) 则电子的自旋运动的描述和轨道角动量的描述相同, S=s(s+1)h
2. 电子自旋 1925年,乌伦贝克和哥德斯密特(当时他俩还是 研究生)在分析上述实验的基础上假设: 电子除了“轨道”运动还有一种内禀的运动,称为 自旋。相应地有自旋角动量S和自旋磁矩μ 。 若自旋“轨道量子数”取 21 s = 则电子的自旋运动的描述和轨道角动量的描述相同, ssS += )1( h (s 称为自旋量子数)
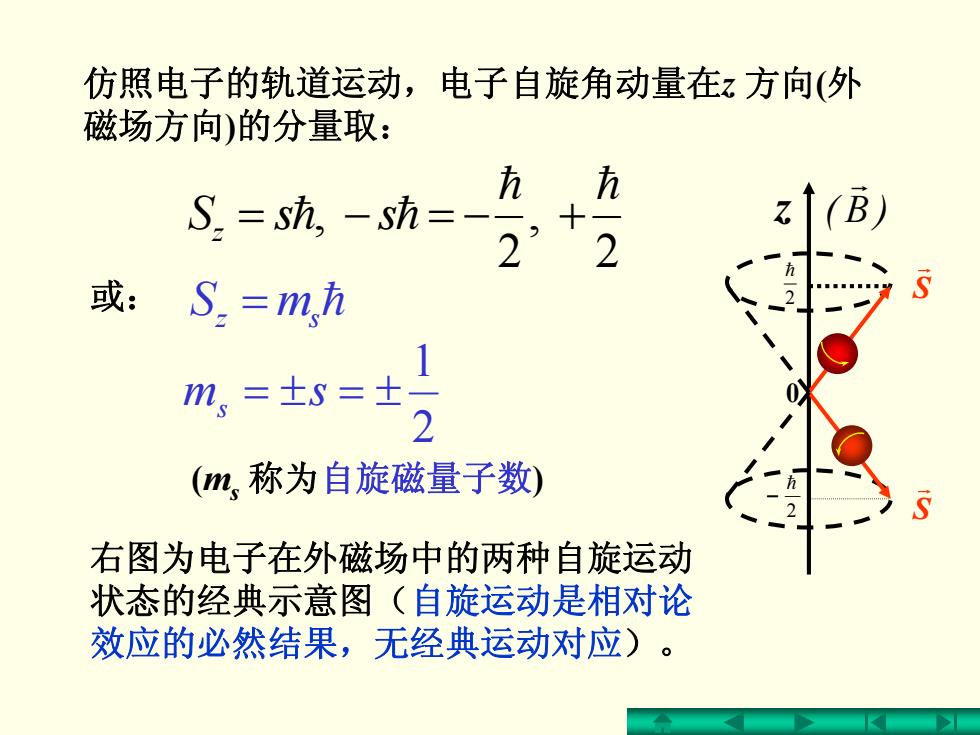
仿照电子的轨道运动,电子自旋角动量在z方向(外 磁场方向)的分量取: S=s吃,-sh= B 2’2 或:S.=m,h m,=士=土1 2 (m,称为自旋磁量子数) 右图为电子在外磁场中的两种自旋运动 状态的经典示意图(自旋运动是相对论 效应的必然结果,无经典运动对应)
仿照电子的轨道运动,电子自旋角动量在z 方向 ( 外 磁场方向 )的分量取: 2 , 2 , hh z ssS hh +−=−= 2 1 s sm ±=±= 或: = mS sz h ( m s 称为自旋磁量子数 ) S r S r )B( r z 2 h − 2 h 0 右图为电子在外磁场中的两种自旋运动 状态的经典示意图(自旋运动是相对论 效应的必然结果,无经典运动对应)