
第4章动量和角动量 §4.1动量定理动量守恒定律 §4.2质心质心运动定理 §4.3碰撞问题 §4.4火箭飞行基本原理 §4.5质点的角动量角动量守恒定律 §4.6质点系的角动量
第 4 章 动量和角动量 §4.1 动量定理 动量守恒定律 §4.2 质心 质心运动定理 §4.3 碰撞问题 §4.5 质点的角动量 角动量守恒定律 §4.4 火箭飞行基本原理 §4.6 质点系的角动量
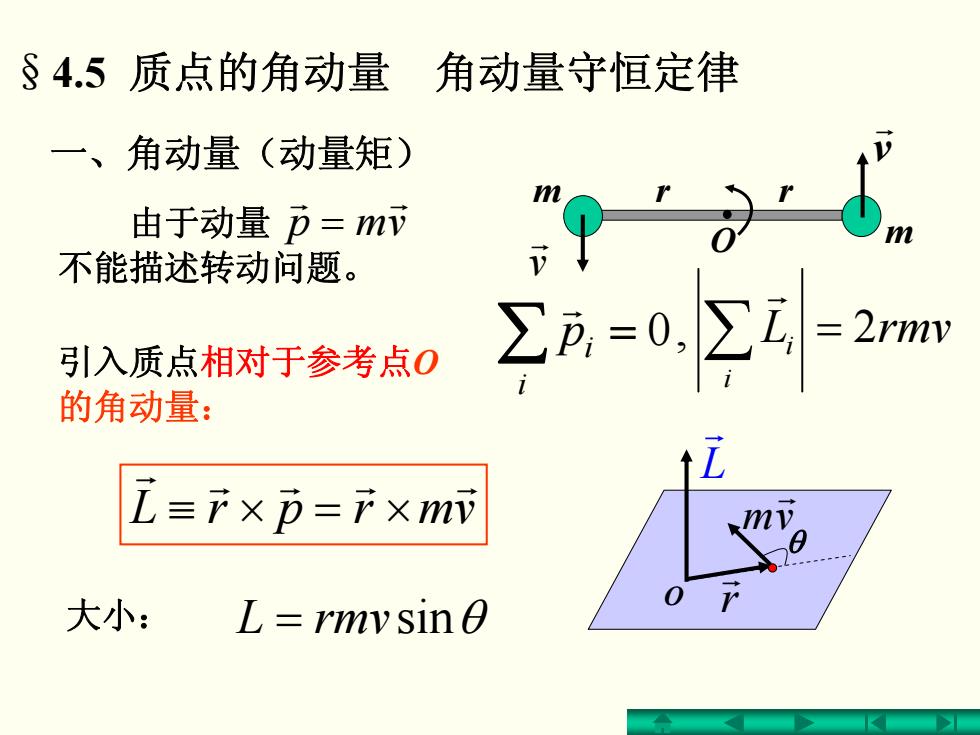
§4.5质点的角动量角动量守恒定律 一、角动量(动量矩) 由于动量p=m币 不能描述转动问题。 引入质点相对于参考点0 ∑元=0,∑-2mw 的角动量: i≡F×p=f×md 大小:L=rmy sin0
一、角动量(动量矩) vmrprL r r r r r ×=×≡ 大小: = rmvL sin θ L r r r vm r θ O §4.5 质点的角动量 角动量守恒定律 引入质点相对于参考点 O 的角动量: ∑ = ,0 i p i r vmpr r 由于动量 = 不能描述转动问题。 O m mr r v r v r rmvL i i ∑ = 2 r

i≡F×p=产×m时 分量式: L ymv:-zmvy Ly zmVx -xmv: L.=xmvy-ymvx Lx,L,L.即质点相对于三个坐标轴的角动量
分量式: z y x y x z x z y ymvxmvL xmvzmvL zmvymvL −= −= = − ,, LLL zyx 即质点相对于三个坐标轴的角动量。 vmrprL r r r r r ×=×≡

二、质点角动量定理 由F= d(mi) dt →F×P=产xd(m di =0 dI d(下×m) d(m)d拉 Xmv dt dt dt =Tx d(mv) =元× dt M 合力对参考点O的力矩: M=产×京 d M=Fd=Frsin0
t vm F d )(d r r = t vm rFr d )(d r r r r ×=×⇒ 合力对参考点O的力矩: 二、质点角动量定理 = = FrFdM sinθ vm t r t vm r t vmr t L r r r r r r r Q ×+×= × = d d d )(d d )(d d d 由 t vm r d )(d r r ×= Fr r r = × =0 F r r r θ d M r M Fr O r r r = ×

M= dt 质点的角动量定理:质点对某固定参考点的角动量的变 化率等于质点所受合力对同一参考点的力矩。 >角动量定理是描述质点转动的动力学方程 Mdt dL (微分形式) Ndr=d=I- (积分形式) ∫Mdt称合力矩在。→1时间内的角冲量或冲量矩
质点的角动量定理:质点对某固定参考点的角动量的变 化率等于质点所受合力对同一参考点的力矩。 t L M d d r r = LtM r r = dd ∫ ∫ −== tt LL LLLtM0 0 dd 0 r r r r r r ¾ 角动量定理是描述质点转动的动力学方程 (微分形式) (积分形式) ∫ tt tM0 d r 称合力矩在 时间内的 0 → tt 角冲量或冲量矩