
第5章刚体力学基础 §5.1刚体运动的描述 §5.2刚体的定轴转动定理 §5.3刚体的转动惯量 §5.4刚体定轴转动的角动量守恒定律 §5.5刚体定轴转动的功能原理 §5.6回转仪进动 §5.7刚体的平面运动
第 5 章 刚体力学基础 §5.1 刚体运动的描述 §5.2 刚体的定轴转动定理 §5.3 刚体的转动惯量 §5.4 刚体定轴转动的角动量守恒定律 §5.5 刚体定轴转动的功能原理 §5.6 回转仪 进动 §5.7 刚体的平面运动

§5.4刚体定轴转动的角动量守恒定律 定轴转动角动量定理:M= d(Jo) dt 当M=0时,有 d(Jo) 0 即J0=J00(常量) 定轴转动角动量守恒定律:刚体在定轴转动中,当 对转轴的合外力矩为零时,刚体对转轴的角动量保 持不变。 适用于刚体,非刚体和物体系
定轴转动角动量定理: ( ) t J M d d ω = 定轴转动角动量守恒定律:刚体在定轴转动中,当 对转轴的合外力矩为零时,刚体对转轴的角动量保 持不变。 适用于刚体,非刚体和物体系。 §5.4 刚体定轴转动的角动量守恒定律 M 0= ( ) 0 。 d d = t Jω 当 时, 有 ω ω00 即 = JJ (常量 )
一、 刚体(J不变)的角动量守恒 若M=O,则Jo=常量,而刚体的J不变,故o的 大小,方向保持不变。 如:直立旋转陀螺不倒。 此时,即使撤去轴承的支撑作用,刚体仍将作 定轴转动一定向回转仪一可以作定向装置
一、 刚体( J 不变)的角动量守恒 若 M=0,则 Jω =常量,而刚体的 J 不变,故 ω 的 大小,方向保持不变。 如:直立旋转陀螺不倒。 此时,即使撤去轴承的支撑作用, 刚体仍将作 定轴转动——定向回转仪—— 可以作定向装置。 o

二、非刚体(J可变)的角动量守恒 J0=J0。=常量 当J增大,o就减小,当J减小,o就增大。 如:芭蕾舞,花样滑冰中的转动, 恒星塌缩(R,)→(R,@)中子星 的形成等
二、非刚体( J 可变)的角动量守恒 当 J 增大,ω 就减小,当 J 减小,ω 就增大。 ω = JJ ω00 = 常量 如:芭蕾舞,花样滑冰中的转动, 恒星塌缩 (R0,ω0) → (R,ω) 中子星 的形成等
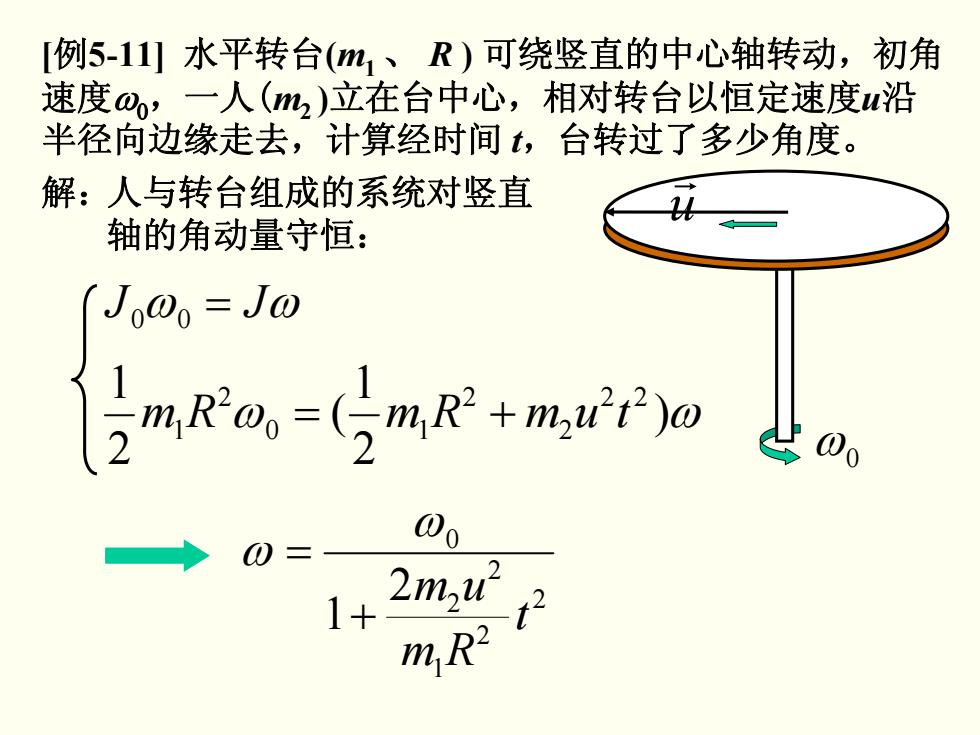
[例5-11]水平转台(m1、R)可绕竖直的中心轴转动,初角 速度@,一人(m2)立在台中心,相对转台以恒定速度u沿 半径向边缘走去,计算经时间,台转过了多少角度。 解:人与转台组成的系统对竖直 轴的角动量守恒: J00=J0 jmR@o=(-mR+mawt)@ 0=- 2mu 1+ 3 mR2
r u ω0 人与转台组成的系统对竖直 轴的角动量守恒: ω00 = JJ ω ω ) ω 2 1 ( 2 1 22 2 2 0 1 2 1 += tumRmRm 2 2 1 2 2 0 2 1 t Rm um + = ω ω [ 例5-11] 水平转台 ( m1 、 R ) 可绕竖直的中心轴转动,初角 速度 ω0,一人( m2 )立在台中心,相对转台以恒定速度 u 沿 半径向边缘走去,计算经时间 t,台转过了多少角度。 解: