
第3章 机械能和功 §3.1功质点动能定理 §3.2保守力非保守力耗散力 §3.3质点在保守力场中的势能 §3.4质点系的势能 §3.5功能原理 能量守恒定律
第 3 章 机械能和功 §3.1 功 质点动能定理 §3.2 保守力 非保守力 耗散力 §3.3 质点在保守力场中的势能 §3.4 质点系的势能 §3.5 功能原理 能量守恒定律
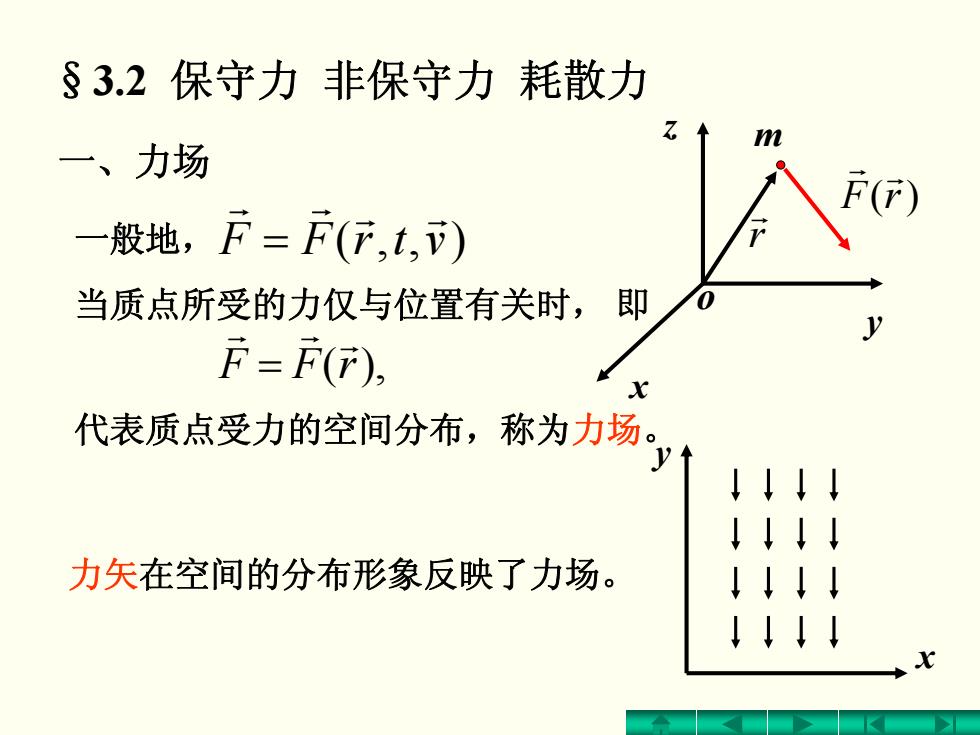
§3.2保守力非保守力耗散力 一、力场 一般地,F=F(行,,) 当质点所受的力仅与位置有关时,即 F=F(), 代表质点受力的空间分布,称为力场。 ↓↓↓↓ ↓↓↓↓ 力矢在空间的分布形象反映了力场。 ↓↓↓↓ ↓↓↓
一、力场 vtrFF ),,(r r r r = x y §3.2 保守力 非保守力 耗散力 力矢在空间的分布形象反映了力场。 x y z r r rF )(r r m o 一般地, rFF ),(r r r = 当质点所受的力仅与位置有关时, 即 代表质点受力的空间分布,称为力场
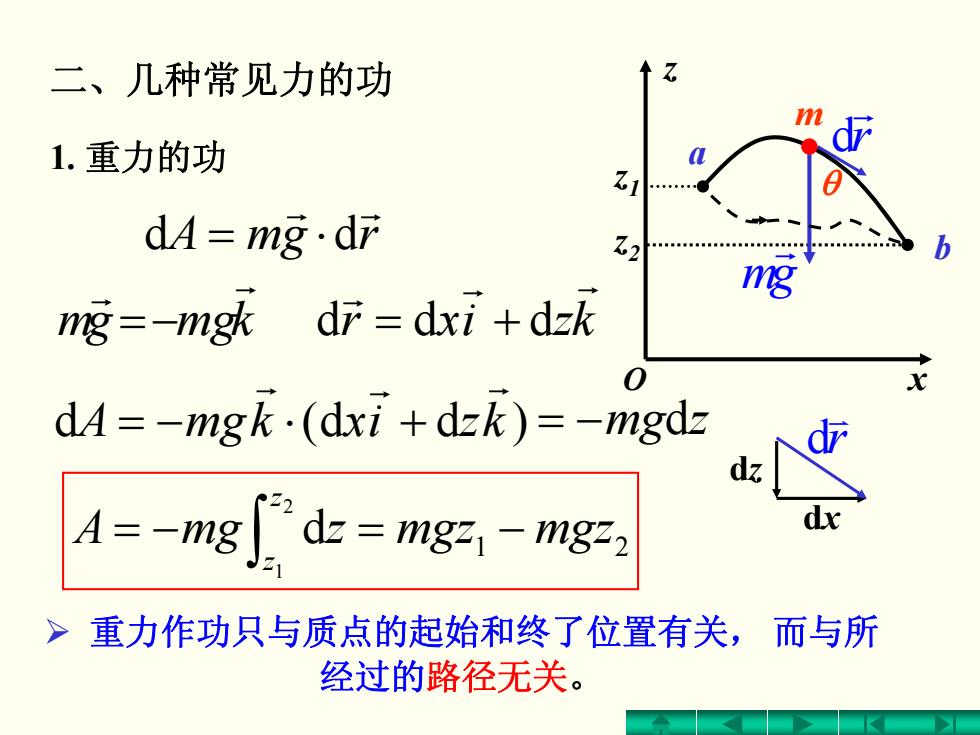
二、几种常见力的功 m 1.重力的功 dA=mg·df ng=-ng欧dF=dxi+dzk 0 dA=-mgk.(dxi+dzk)=-mgdz dz 4=-mg"d==mgz mgz2 重力作功只与质点的起始和终了位置有关,而与所 经过的路径无关
二、几种常见力的功 1. 重力的功 rgmA r r = ⋅dd kmggm r r −= kzixr r r r += ddd d kzixkmgA )dd( r r r +⋅−= 1 2 2 1 d mgzmgzzmgA z z −=−= ∫ ¾ 重力作功只与质点的起始和终了位置有关, 而与所 经过的路径无关 。 r v d d z dx z r r d θ gm r z 1 z2 a b m O x = − dzmg

2.万有引力的功 设质量为M的质点固定,另一质量为m的质点在M的引 力场中从a点运动到b点。 Mm F=-G A-d r+dr 7.d=rdcosa rdr >万有引力的功仅由物体的始末位置决定,而与路径无关
2. 万有引力的功 设质量为M的质点固定,另一质量为m的质点在M的引 力场中从a点运动到b点。 r r Mm GF r r 3 −= ∫ ⋅−= b a r r rr r Mm GA rr d 3 =⋅ α = dcosdd rrrrrrr r r ) 11( d2 ba r r rr GMm r r GMmA b a −= −−= ∫ dr rr r r + d r r α d ¾ 万有引力的功仅由物体的始末位置决定,而与路径无关。 rb ra a b M m r r F v
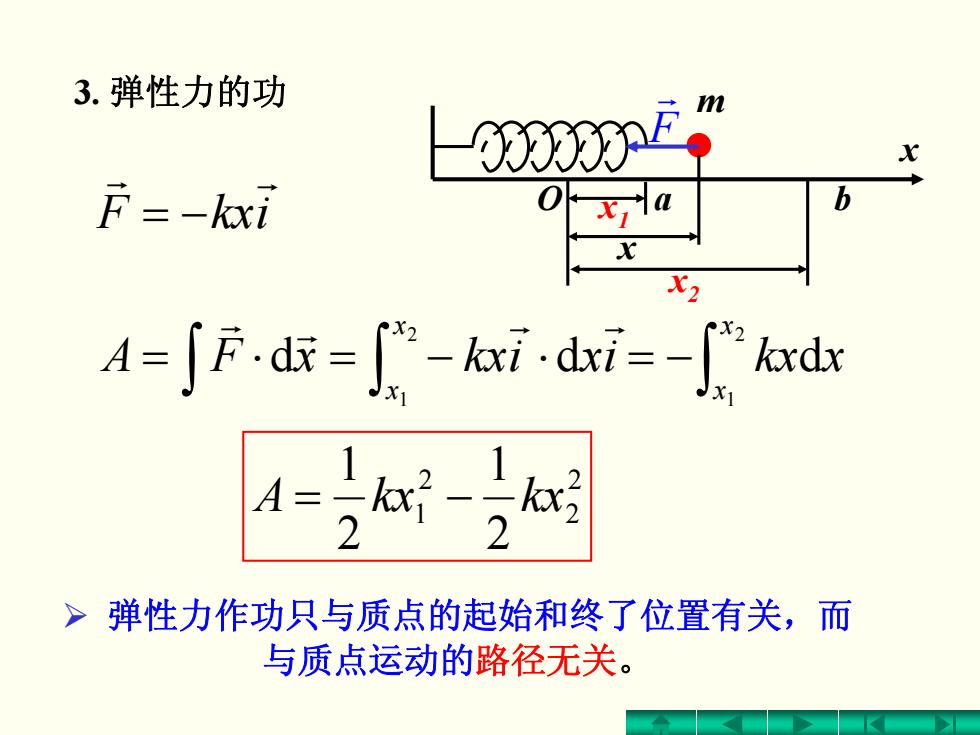
3.弹性力的功 0000355 F=-kxi t,J =dexdx kordz A- >弹性力作功只与质点的起始和终了位置有关,而 与质点运动的路径无关
3. 弹性力的功 ikxF r r −= ∫ ∫ ⋅−=⋅= 21 d d xx ixikxxFA r r r r 2 2 2 1 2 1 2 1 −= kxkxA ¾ 弹性力作功只与质点的起始和终了位置有关,而 与质点运动的路径无关。 x m x2 x1 O a b x F r ∫ −= 21 d xx xkx