
第22章量子力学基础 §22.1实物粒子的波动性 §22.2波函数及统计解释 §22.3不确定性关系 §22.4薛定谔方程 §22.5力学量算符的本征值问题 §22.6薛定谔方程的应用 §22.7氢原子量子理论 §22.8电子的自旋泡利不相容原理
§22.1 实物粒子的波动性 §22.2 波函数及统计解释 §22.3 不确定性关系 §22.4 薛定谔方程 §22.6 薛定谔方程的应用 §22.5 力学量算符的本征值问题 §22.7 氢原子量子理论 §22.8 电子的自旋 泡利不相容原理 第 22 章 量子力学基础

§22.7氢原子量子理论 氢原子中的电子在中心力场中运动 Ur)=- e2 4元8' 2+U 2m 采用球坐标系 h2 1 6 2 2mr20r' +U(r)
§22.7 氢原子量子理论 氢原子中的电子在中心力场中运动 U m H +∇−≡ 2 2 2 ˆ h r e rU 0 2 4π )( ε −= )( 2 ˆ 1 2 ˆ 2 2 2 2 2 rU mr L r r rrm H ⎟ ++⎠⎞ ⎜⎝⎛ ∂∂ ∂∂ −= h 采用球坐标系

其中2为电子绕核的轨道角动量平方算符 L,的为轨道角动量在方向的分量: ∂ L:=-ih 一、角动量算符的本征值问题 通过求解2和,的本征方程得到本征函数和本征 值如下(过程略):
θθ θ θθ 2 2 2 2 sin ˆ sin sin ˆ Lz L ⎟ +⎠⎞ ⎜⎝⎛ ∂∂ ∂∂ −= h ∂ϕ ∂ −= ih ˆ L z 一、角动量算符的本征值问题 其中L2为电子绕核的轨道角动量平方算符 Lz的为轨道角动量在z方向的分量: 通过求解L2和Lz 的本征方程得到本征函数和本征 值如下(过程略):
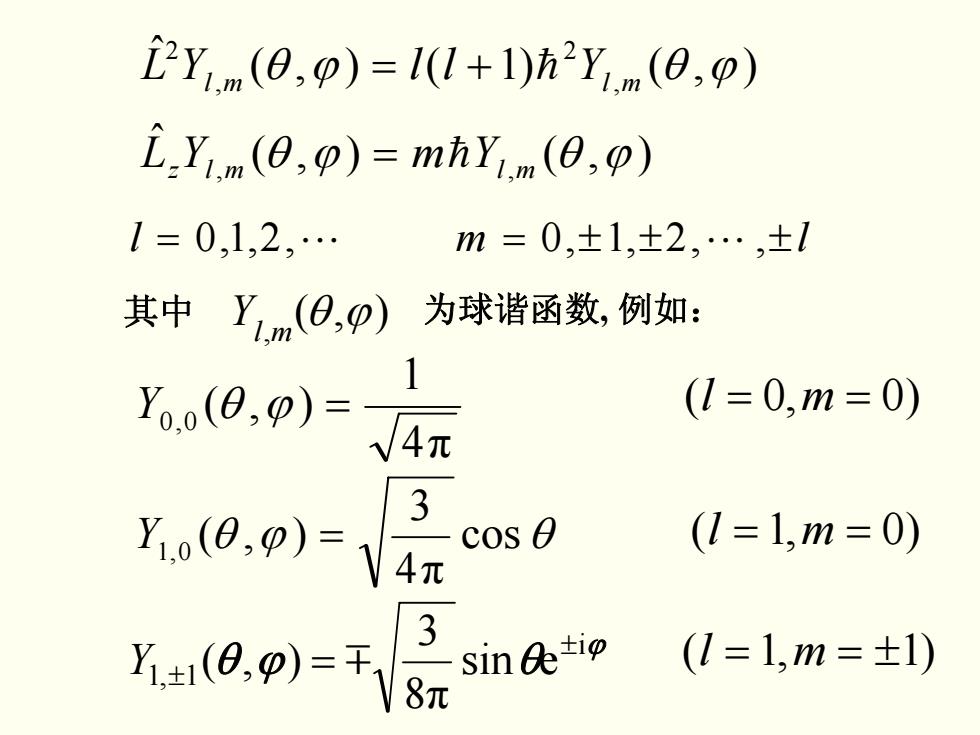
2Ym(0,p)=1(1+1)h2Y.m(0,p) i.Y,m(0,p)=mhY.m(0,p) 1=0,1,2,… m=0,±1,±2,…,±l 其中Ym(O,p)为球谐函数,例如: Yo.0(8,p)= (1=0,m=0) 3 Y(0,p)=4元 cos 0 (1=1,m=0) 3 Y±(8,p)=干 sin ti (1=1,m=±1) 8元
l = ,2,1,0 L m = ± ± L ,,2,1,0 ±l ),()1(),( ˆ , 2 , 2YL ml ϕθ += h Yll ml ϕθ ),(),( ˆ YL ,mlz ϕθ = hYm ,ml ϕθ 其中 ),( , θ ϕ ml Y 为球谐函数, 例如: 4π 1 ),( Y 0,0 ϕθ = = ml = )0,0( = ml = )0,1( = ml = ± )1,1( ϕθ cos θ 4π3 ),( Y 0,1 = ϕ ϕθ θ i 1,1 esin 8π3 ),( ± Y ± = m

1.主要结论 ·和L,有共同的本征函数Y,m(O,p) 。的本征值为 L2=1(1+1)h2 =0,1,2..称为角量子数。 角动量的大小:L=V√1(1+1)方 =0,√2h,V6h, 角动量L的取值是量子化的(量子力学很自然地给出角 动量的量子化),最小值可取零(与玻尔假设不同)
llL += )1( h 角动量L的取值是量子化的(量子力学很自然地给出角 动量的量子化),最小值可取零(与玻尔假设不同)。 1. 主要结论 • 和 有共同的本征函数 Yl, m(θ,ϕ) 2 Lˆ Lz ˆ • 的本征值为 2 Lˆ 2 2 llL += )1( h l=0,1,2… 称为角量子数。 角动量的大小: = hh ,...6,2,0