
核心重难探究 思路点拨:1)把 分别代入y=-x2+bx+c中得到关于 b,c的方程组,解方程组即可得到b,c的值;然后计算x= 时y的值即可得到n的值;2)利用表中数据求解 导航页
导航页 核心重难探究 思路点拨:(1)把 分别代入y=-x 2+bx+c中得到关于 b,c的方程组,解方程组即可得到b,c的值;然后计算x= 时y的值即可得到n的值;(2)利用表中数据求解

核心重难探究 解:1)根据表格数据可得 -4-2b+c=5,解得 b=-2, -1+b+c=2, c=5. ∴y=-x2-2x+5. 当x=-1时y=-x2-2x+5=6,即n=6. (2)根据表中数据得当0≤x≤2时,y的最大值是5. 【方法归纳】 根据所给的表格求二次函数关系式时,要仔细观察表格中的 数据,选择恰当的数据代入数值求解 导航页
导航页 核心重难探究 解:(1)根据表格数据可得 -𝟒-𝟐𝒃 + 𝒄 = 𝟓, -𝟏 + 𝒃 + 𝒄 = 𝟐, 解得 𝒃 = -𝟐, 𝒄 = 𝟓. ∴y=-x 2 -2x+5. 当x=-1时,y=-x 2 -2x+5=6,即n=6. (2)根据表中数据得当0≤x≤2时,y的最大值是5. 【方法归纳】 根据所给的表格求二次函数关系式时,要仔细观察表格中的 数据,选择恰当的数据代入数值求解
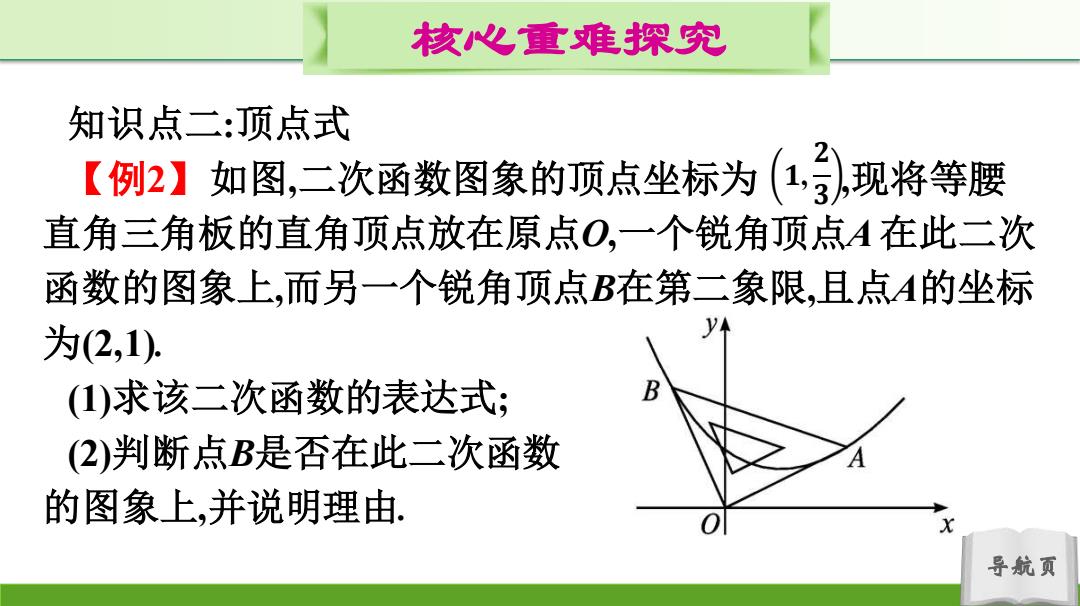
核心重难探究 知识点二:顶点式 【例2】如图,二次函数图象的顶点坐标为(1,现将等腰 直角三角板的直角顶点放在原点O,一个锐角顶点A在此二次 函数的图象上,而另一个锐角顶点B在第二象限,且点A的坐标 为(2,1). (1)求该二次函数的表达式; (2)判断点B是否在此二次函数 的图象上,并说明理由. 导航页
导航页 核心重难探究 知识点二:顶点式 【例2】如图,二次函数图象的顶点坐标为 ,现将等腰 直角三角板的直角顶点放在原点O,一个锐角顶点A 在此二次 函数的图象上,而另一个锐角顶点B在第二象限,且点A的坐标 为(2,1). (1)求该二次函数的表达式; (2)判断点B是否在此二次函数 的图象上,并说明理由. 𝟏, 𝟐 𝟑