
定积分的应用 第五章 单变量函数的积分学 参数曲线的弧长 设曲线由参数方程 8as例给甜,脚a0w在 [a,B]上有连续导数.弧长微元为: ds =/(dx)2+(dy)2=()+w(t)di. 故弧长为:s=∫Vp()+y()d 特别地,对极坐标曲线r=r(θ)(≤0≤),设r(0)连续可导,则 曲线有参数化(x,y)=(r(0)cosO,r(0)sinO),代入上式可得: s=vf产(0)+(f(ada. 7
7 定积分的应用 第五章 单变量函数的积分学 设曲线由参数方程 给出,其中 在 参数曲线的弧长 : 上有连续导数. 弧长微元为 : 故弧长为 : 特别地,对极坐标曲线 设 连续可导,则 曲线有参数化 代入上式可得 :

定积分的应用 第五章 单变量函数的积分学 3 2 1.求曲线y=一x2上相应于x从1到2的一段弧的长度, 3 2.求旋轮线x=a(t-sint),y=a(1-cost)一支的弧长. x2 3.求椭圆 21的周长 8
8 定积分的应用 第五章 单变量函数的积分学 2. 求旋轮线 一支的弧长. 1. 求曲线 上相应于 从1到2的一段弧的长度. 3. 求椭圆 的周长
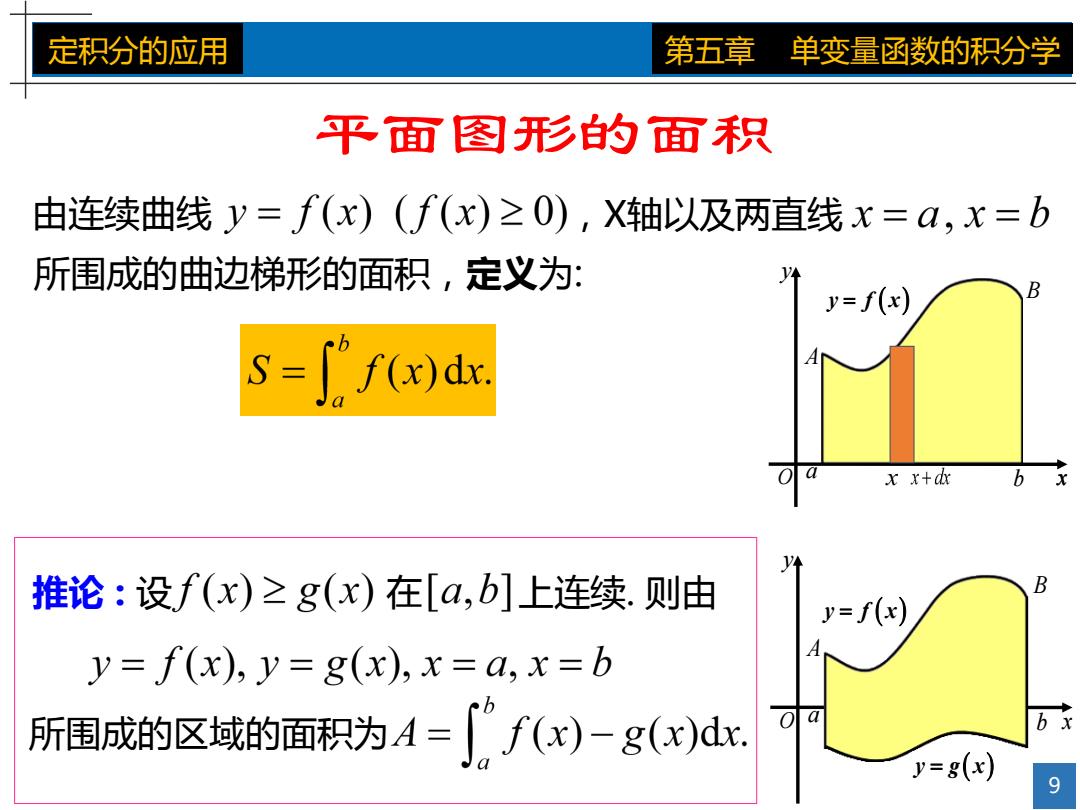
定积分的应用 第五章 单变量函数的积分学 平面图形的面积 由连续曲线y=f(x)(f(x)≥0),X轴以及两直线x=a,x=b 所围成的曲边梯形的面积,定义为: y=f(x) S=∫fx)dx xx+dx 6 推论:设f(x)≥g(x)在[a,b]上连续.则由 B y= f y=f(x),y=g(x),x=a,x=b 所围成的区域的面积为A=f(x)-g(x)dx y=g(x) 9
9 定积分的应用 第五章 单变量函数的积分学 平面图形的面积 由连续曲线 ,X轴以及两直线 所围成的曲边梯形的面积,定义为: 推论 : 设 在 上连续. 则由 所围成的区域的面积为 b a x A B x y O y f x y O x A B b a y g x y f x