
练习:解二元线性方程组 3x1-2x2=12 2x+x2=11 解: D= 3-2 21 =3-(4)=7+0, D,= 12 =-21, 14 X1= D. -21-3. D 7 上页
. 2 1 3 2 12 1 2 1 2 + = − = x x x x 2 1 3 − 2 D = 1 1 12 2 1 − D = = 14, 2 1 3 12 D2 = = −21, D D x 1 1 = 2, 7 14 = = D D x 2 2 = 3. 7 21 = − − = 练习: 解二元线性方程组 解: = 3 – (–4) = 7 0

三阶行列式 用高斯消元法,解三元一次线性方程组 a11+a12x2+a3x3=b a21X+a22X2+a23x3=b2, (1.2) a31+a32x2+a33x3=b 也可以得到类似二元一次线性方程组的结果。 即如果引入三阶行列式 11 412 13 D 421 42 23 031 32 33 列标 行标 上页 这回
用高斯消元法,解三元一次线性方程组 也可以得到类似二元一次线性方程组的结果。 (1.2) 三阶行列式 列标 行标 即如果引入三阶行列式

则当(1.2) 的所有行列式 du 12 413 6 a12 a D= L22 a23 ≠0 D- b, a22 32 133 b, 432 a33 b a13 a11 a12 b D2 5% b2 a23 D3= a21 a22 a31 b a33 a32 方程组(1.2)的解可以用三阶行列式表示为
11 12 13 21 22 23 31 32 33 0 a a a D a a a a a a = 方程组(1.2)的解可以用三阶行列式表示为 , , . 3 3 2 2 1 1 D D x D D x D D x = = = 3 32 33 2 22 23 1 12 13 1 b a a b a a b a a D = 31 3 33 21 2 23 11 1 13 2 a b a a b a a b a D = 31 32 3 21 22 2 11 12 1 3 a a b a a b a a b D = 则当(1.2)的所有行列式

三阶行列式的计算 (1)对角线法则 =41122433+41223031+013421032 13223厂012L21L334112332: 注意:红线上三元素的乘积冠以正号,蓝线上三元 素的乘积冠以负号. 说明1.对角线法则只适用于二阶与三阶行列式 说明2.三阶行列式包括3!项,每一项都是位于不 回
三阶行列式的计算 11 22 33 = a a a . 11 23 32 − a a a (1)对角线法则 13 21 32 + a a a 12 23 31 + a a a 13 22 31 − a a a 12 21 33 − a a a 31 32 33 21 22 23 11 12 13 a a a a a a a a a 说明2. 三阶行列式包括3!项, 每一项都是位于不 同行, 不同列的三个元素的乘积, 其中三项为正, 三项 为负. 注意:红线上三元素的乘积冠以正号, 蓝线上三元 素的乘积冠以负号. 说明1. 对角线法则只适用于二阶与三阶行列式.
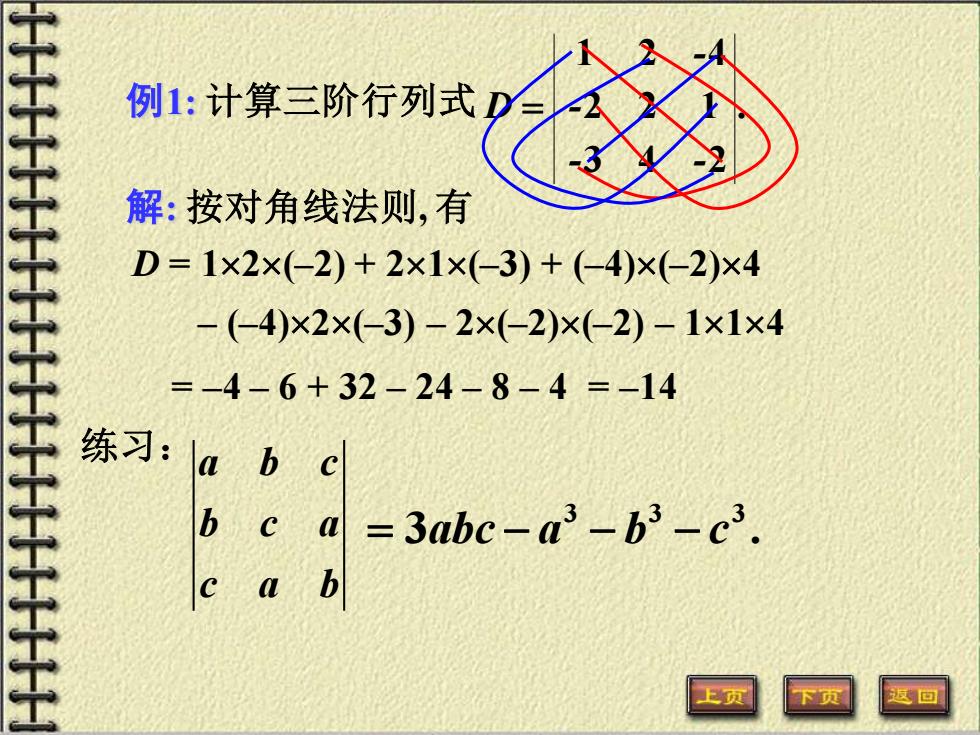
例1:计算三阶行列式 解:按对角线法则,有 D=1×2×(-2)+2×1x(-3)+(-4)×(-2)×4 -(-4)×2×(-3)-2×(-2)×(-2)-1×1×4 =-4-6+32-24-8-4=-14 练习: a b c b c =3abc-a3-b3-c3. e a b 上页
. 3 4 2 2 2 1 1 2 4 - - - - 例1: 计算三阶行列式 D = 解: 按对角线法则, 有 D = 12(–2) + 21(–3) + (–4)(–2)4 – (–4)2(–3) – 2(–2)(–2) – 114 = –4 – 6 + 32 – 24 – 8 – 4 = –14 练习: abc b c a c a b 3 3 3 = − − − 3 . abc a b c