
这个积分已在例题4.5.3计算出了。在那里,确定了带电满带的二这样,用0/gpK,(4.524)式即变成所求的矢量位。等值4,曲面的剖面示于图8.1.1.记咨这些也就是磁通密度uH线。例 8. 1. 2 二维的磁偶极子场图8.1.2 示出--对载有显值为反方向电流的很接近的导体。电流搭z方商流向+初一无限远,阅此,最终的场是:二维的并且能用 A,来插述。在极坐标系中,从右边导体 (它离开 ≥ 轴的距离是 4)到观察点的距离近似地为acoap。每个导线的A,都取(16)式的形式,这里,从导线到观察点的距离。这样,把两根导线产生的尖最位相叠加给出(19)[1a (-dcos0)-Inr]--n(1-cos0)A8在极限dr时,这个表达式变成A d(20)这样,等值A,曲面与常值之平面的相交线是一族,如图8.1.3所示。这些球密度线,这可由(17)式导出(ng+sd)(21)uHo如果用线电荷代替线电流,则得到的等位线(即等位面与4-4平面的相交线)与图8.1,3所示均线相重合。因此,图8.1.3中所示磁构型的电对偶的电场强度钱沿着与所示典线相垂直的曲线,起始于右边的正线电围8.1.3等俏4,曲的机钱面,扭即是图8.1.2构型的磁通密度线荷,而终止于左边的负线电荷。8.2毕奥沙伐重叠积分经从8.1节的重叠积分确定了矢量位,即可由curIA计算出磁通密度。然而在某些场的计算中,最好是对场本身有一个重叠积分公式。例如,在数值计算中,数值导数应该避免。在进行积分计算之前,对(8.1.8)式给出的尖量位求旋度可得出场的选加积分式J(r')ldH-xA=V×J(1)这个积分是对源坐标r'进行的,而旋度运算涉及到对观察点坐标「求导数。因此,可在进行积!分计算之前,先进行旋度计算,这样(1)式变成H=, []ao(2)为了求取这个表达式中被积函数所需要的cur1运算可以进行,而不用考虑电流密度的特定分布,这是因为导数是对r的而不是对r"的。为了进行这一计算,注意到curl是对矢量J和标量—{r-r"-的乘积的运算。这-运算遵循矢疑恒等式×()=× x(3)中FJ与无关,上式右边第一项是零。因此,(2)式成为()xJdo(4)+241
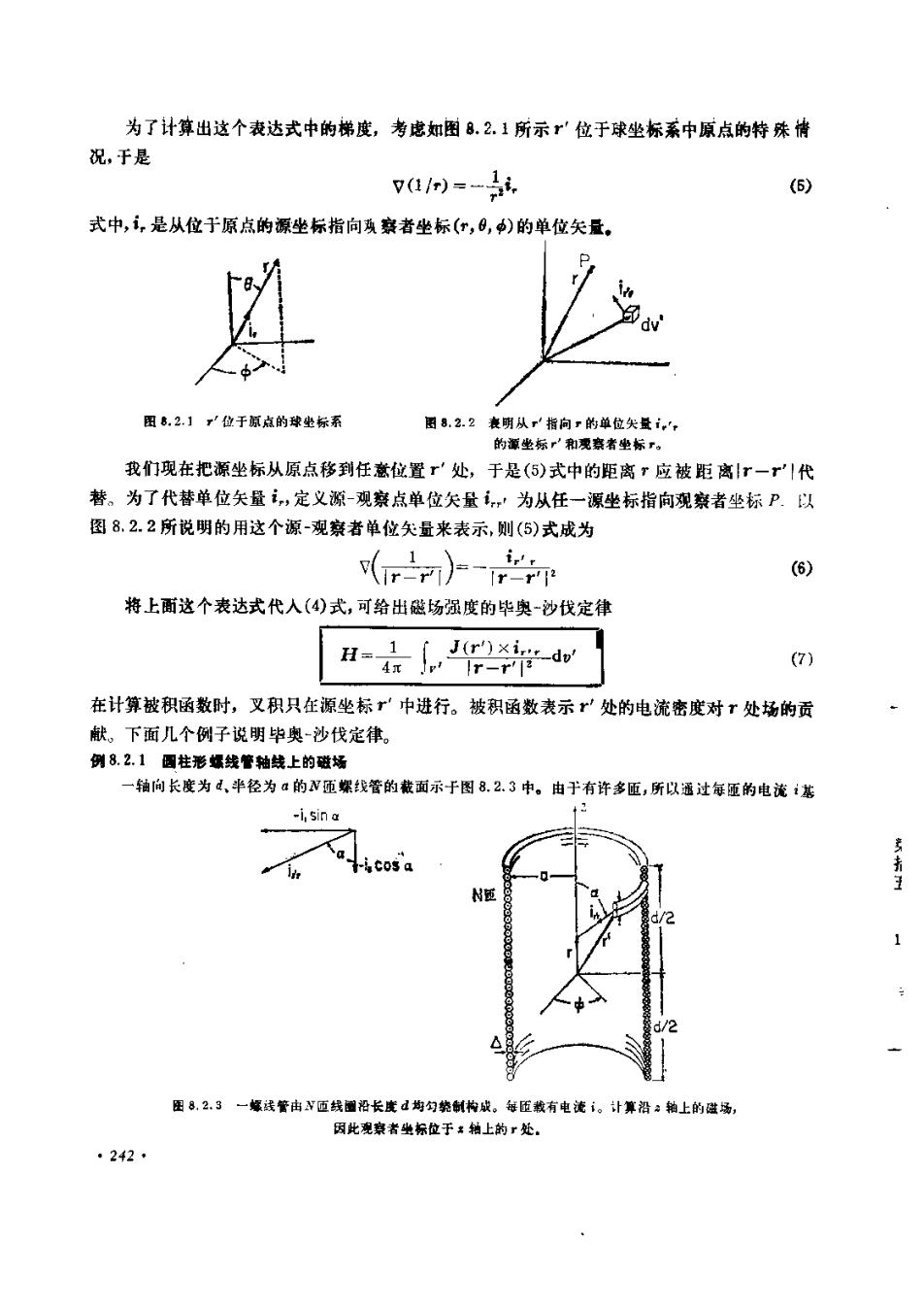
为了计算出这个表达式中的梯度,考虑如图 8.2. 1 所示 r 位于球坐标系中原点的特殊情况,于是v(1/0)=-1i.(6)式中,i,是从位于原点的源坐标指向观察者坐标(r,,$)的单位矢盈。图8.2.1位于原点的球坐标系图 8.2. 2 明从 指向=的单位尖量 i, ,的源坐标和观察者坐标。我们现在把源坐标从原点移到任意位置r处,于是(5)式中的距离,应被距离Ir一r代替。为了代替单位矢量i,定义源-观察点单位欠量 i,为从任一源坐标指向观察者坐标 P。以图 8. 2. 2 所说明的用这个源-观察者单位欠量来表示,则(5)式成为(6)(1r-)--re将上面这个表达式代入(4)式,可给出磁场强度的毕奥-沙伐定律 2-d(7)在计算被积函数时,又积只在源坐标r中进行。被积函数表示r"处的电流密度对r处场的贡献。下面几个例子说明毕奥-沙伐定律。例 8.2.1 固柱形螺线管轴线上的磁场一轴长度为 4、半径为 α的N还螺线管的截面示于图 8.2.3 中。 由于有许多匠,所以遥过每匾的电流 1基i,sir新MNE1上沿抽上的造因此观察者坐标位于轴上的处·242·

本上是沿方向的。为了使积分简单起见,我们只展于求之轴上的 H,2辅是对称轴。在圆柱坐标系中,源坐标增量体积元d=r'da'ar'd2。对于一均勾分布在厚度A上的许多线圈来说,电流密度基本上为总匝数乘以每區电流再除以电流流过的面积JEiN(8) 殖叠积分(7)式首先对"进行计算。这个积分的计算区间是沿线函的径向厚度从=a到"=α+A。因为A≤α,所以在这个间隔内,源点到观察点的距离及方向谌本上保持为常值。因此,此积分等于被^相乘的乘积。轴对称性要求z轴上的H应沿z方向。对z和的积分是-ad'da(9)H,-(a)用图8.2.3示出的角度α和它的余角来表示,源-观察点单位失且是(10)i,,--i.nina-i,osa因此(11)(igxir)r2+(72)(9)式中的被积函效与无关,则对中的积分等于乘以 2元2d(12)H.-2J2[a+(22)42利用替换关系"可得量一兴一三2+三(13)H.-NAh-(a-)+(%+)在d/2a1的极限下,螺线管变成中心位于z=0平面的平径为。的N匝μ形线。这个线圈中心处的磁场可由(13)式求得为等于安伍数除以圆环直径H-Ni(14)达样,~个具有乎径a=5cm(比它的轴向长度&大),匝数为100匝的载电流i=1A的圆环,其中心处的磁场强度将是 1000 A /m。 此时,磁强计测得的磁通密度是 B,=μl1,=4n×10-7(1000)T=4元Gs。主下面演示中,将进一步讨论这一结果的含意。演示8. 2.1 显柱形螺线管的磁场图8.2.4所示螺线管有N=141巨,轴向长度d=70.5cm,半径a=13.6cm。歪尔型磁强计用来测量线圈内部及其周国H的盘值和方向。图8.2.4示出当实验线照的长度对直径之比为4/2g=2.58时,由(13)式计算出的H,沿轴分布。如果1A,中心处的磁通密度接近2.5Gs。理论值和实验值符合的精度很可能受象探戴尔强20回I图8.2.4记录例惠七开,的侧雨图· 243 *

头所放位暨和滋强计的校准等的限制。还须满足在线阖邻近没有磁化材料(例如铁)的要求。为了避免舱球磁场的影响(数最级约为1高斯),应该使用交流场。如果使用交流场,附近不应该有其中可能感应出涡流的大块导体存在(本书下面两章将分别讨论磁化和涡流)无限长螺线管可看作是“平行板电容器”在MQS系统中的类比。正如电容器可被假成在两板间能产生均电场,而在板外区域的电场为零一样,长螺线管在其内部区域也会产出一均句磁场,而外部场是零。这可从探察到的场不仅足轴胞位置的菌数,而且也是半径的函数著出。对于有限长螺线管,图 8. 2. 4 中的沿轴的内部场用H。表示,在它轴上/2》处的值由(13)式给出(15)+H=[+(a/2a)-]在螺线管长度也远远大于它的乎径的极限下,即&/2a》1,这个表达成为H.---Ni/d(16)磁场测量表明场化内部截面上各点也都保持(16)式的值和方向。它也表明在线图外部沿轴向离端部数倍半径a 处,磁场强度相对地很小。通连续性要求沿≥轴方向穿过螺线管的总磁通必须在螺线管外部沿一α方向返回。那末,长螺线管的外部磁场与内部场相比为多大时才能够忽略呢1外磁道沿一α方向返回时所穿过的面积比内磁通所案过的面积元”大得多。事实上,当线图变成无限长时,这个返回磁通扩展在沿和方向都伸向无限远的外部面积上,当线圈做得非常长时,线图外部磁场糙于零,计算电磁铁磁场的棒模型对于为数不多的构型可以解析地完成毕奥-沙伐重叠积分。然而,它的计算差不多相当于求每个电流元对场的贡献之和。这样,在计算机上,它的计算是一件直截了当的事情。许多实际电流分布是或者可近似为相连接的许多直线电流段或电流“棒”。现在,我们将利用毕奥-沙伐定律求与任愈位置的一电流棒相关的在观察位置 r处的磁场。这个结果是一个有实效的办法,因为对微分体积电流元的数值求和可用对椿的数值求和来代替。图8.2.5所示的电流棒可用一矢量α来表示。这样,电流在这个矢量的底端r+b和顶端r十c之间星均勾分布。源坐标r沿着电流棒。下面儿段内容的目的是沿电流捧长度进行积分,并得到 H(r)的表达式。由于在它的两端,电流棒并不表示无数的电流密度,只有当它与其它电流棒相连接后共同表示一连续的电流分布时,所求得的场才有物理意义。EE=E电统格泰者位量E-t,-9E-O图8.2.5一线电流沟勾分布在起始于+b终止于+。图8.2.6图8.2.5的电流元在包含c、6的欠盘a的长度上,要确定观察点,处的避场强以及。的平面上的視域· 244

电流棒的详细外观,图8.2.6表明源坐标专表示沿着棒的位置,这个坐标的源点位于棒的延长线上离观察点最近处。b在矢最a上的投影是=a·b/!al。这样,如图8.2.6所示,电流棒的起始点与多=0的距离是,而终止在距离为。处,c在a轴上的投影也示于图中。叉积c×a/lal垂直于图8.2.6的平面,其模等于c在位于图8.2.6的平面内且垂直于a的某一矢量上的投影。这样,观察者的位置和电流体轴线间的最短距离是=c×al/αl。由这一事实和义积的定义可得出[cxa]dsxs(17)这里ds是沿着线电流的微分,且Ir-r'l=(g+r)ua对毕奥-沙伐定律(7)式的积分首先在棒的截面上进行。由于截面的几何尺寸很小,因此在7进行积分的过程中被积函数基本上保持常值。这样,电流密度可以代之以总电流,并丑积分可化为沿着棒的轴向坐标的积分H-去[受新"丰5(18)考虑到(17)式,这个积分可用源坐标积分变量专表示成xad(19)H-.a+:完成这个积分可得H-t[ (20)静当在积分端点计算这个表达式时,注意到根据定义式(8% +)1/2 =lcl, (%- ) 1/2 =b)(21)风此,(20)式成为用确定电流棒的相对位置的矢量a、b 和tc表示的观察者位置处的场强表达式。[=exa (-)(22)以下说明如何可将这个表达式反复地用于确定由电流棒以分段形式描述的电流所产生的磁场。如果选而笛卡儿坐标表示的话,矢量是规定构成一复杂绕组的一些电流棒的一个方便工具。在计算机上,(22)式的计算可用一个可以使用许多次的子程序方便地完成。例题 8.2. 2一对正方形线圈的轴向磁场图8.2.7示出一对正方形线圈,每个线图都有N匠且裁有电流。电流沿这样的方向流动使每个线照沿·245