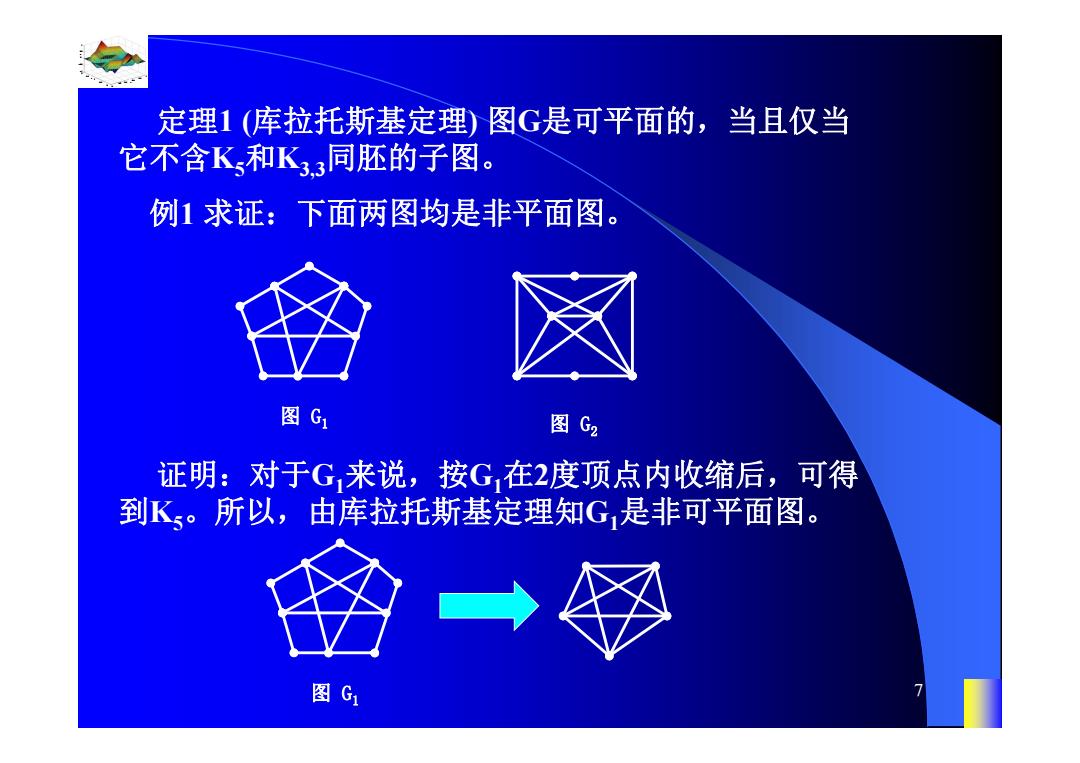
定理1(库拉托斯基定理)图G是可平面的,当且仅当 它不含K和K.3同胚的子图。 例1求证:下面两图均是非平面图。 图G 图G2 证明:对于G,来说,按G,在2度顶点内收缩后,可得 到K。所以,由库拉托斯基定理知G,是非可平面图。 图G
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 7 定理1 (库拉托斯基定理) 图G是可平面的,当且仅当 它不含K5和K3,3同胚的子图。 例1 求证:下面两图均是非平面图。 图 G1 图 G2 证明:对于G1来说,按G1在2度顶点内收缩后,可得 到K5。所以,由库拉托斯基定理知G1是非可平面图。 图 G1
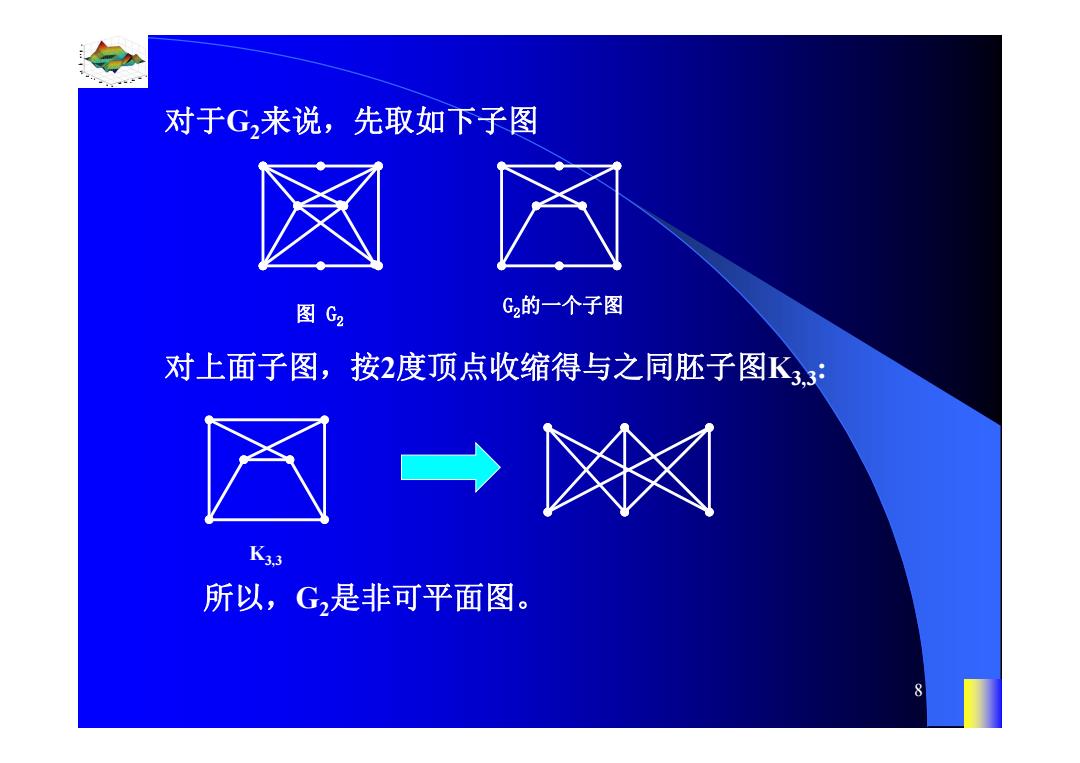
对于G,来说,先取如下子图 图G2 G2的一个子图 对上面子图,按2度顶点收缩得与之同胚子图K,3 → 飞3 所以,G是非可平面图。 8
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 8 对于G2来说,先取如下子图 G2的一个子图 对上面子图,按2度顶点收缩得与之同胚子图K3,3: K3,3 所以,G2是非可平面图。 图 G2
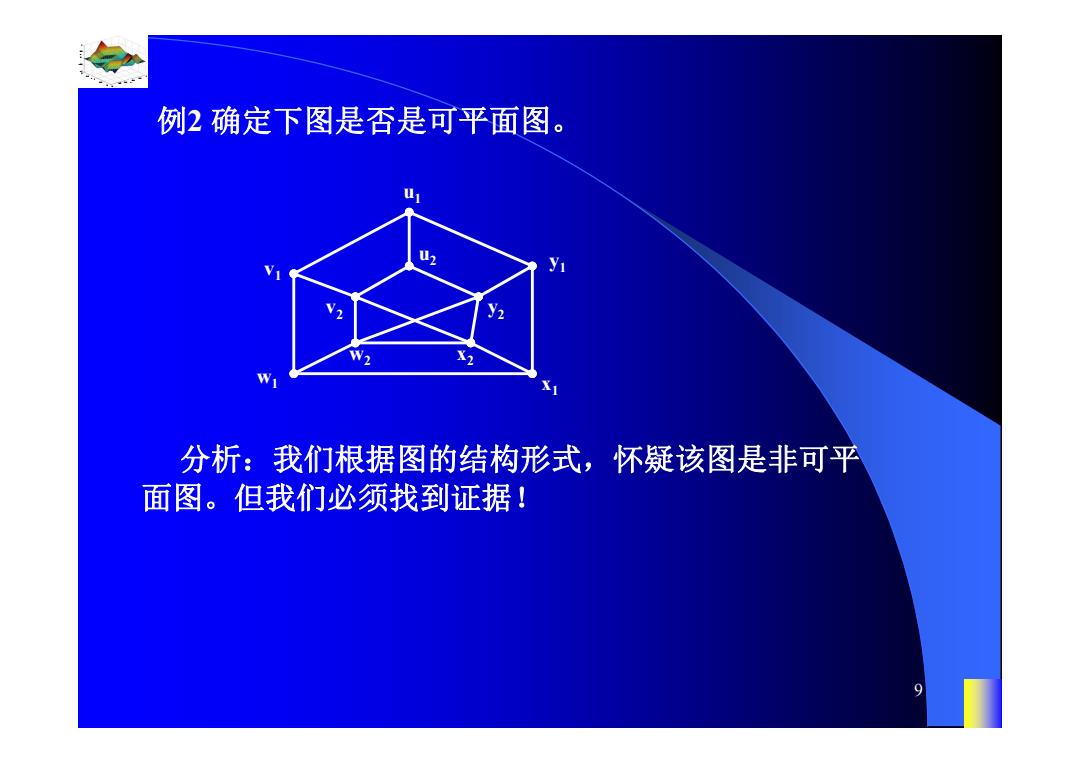
例2确定下图是否是可平面图。 分析:我们根据图的结构形式,怀疑该图是非可平 面图。但我们必须找到证据!
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 9 例2 确定下图是否是可平面图。 u1 u2 v1 v2 y1 y2 x1 x2 w1 w2 分析:我们根据图的结构形式,怀疑该图是非可平 面图。但我们必须找到证据!
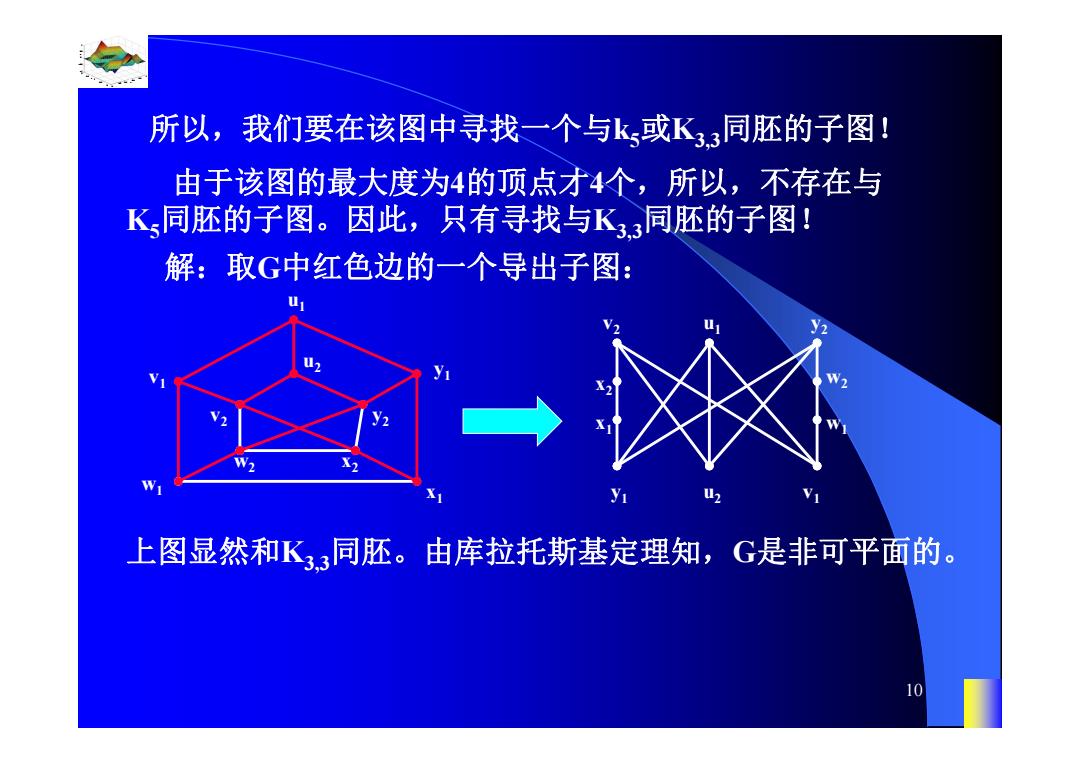
所以,我们要在该图中寻找一个与k或K33同胚的子图! 由于该图的最大度为4的顶点才4个,所以,不存在与 K同胚的子图。因此,只有寻找与K3同胚的子图! 解:取G中红色边的一个导出子图: u 2 上图显然和K33同胚。由库拉托斯基定理知,G是非可平面的。 10
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 10 u1 u2 v1 v2 y1 y2 x1 x2 w1 w2 所以,我们要在该图中寻找一个与k5或K3,3同胚的子图! 由于该图的最大度为4的顶点才4个,所以,不存在与 K5同胚的子图。因此,只有寻找与K3,3同胚的子图! 解:取G中红色边的一个导出子图: u1 u2 v1 v2 y1 y2 x1 x2 w1 w2 上图显然和K3,3同胚。由库拉托斯基定理知,G是非可平面的

注:1) 库拉托斯基定理可以等价叙述为: 库拉托斯基定理:图G是非可平面的,当且仅当它含有 K或K3.3同胚的子图。 (2)库拉托斯基(1896--1980)波兰数学家。1913年开始 在苏格兰格拉斯哥大学学习工程学,1915年回到波兰发沙 大学转学数学,主攻拓扑学。1921年获博士学位。1930年 在利沃夫大学作数学教授期间,发现并证明了图论中的库 拉托斯基定理。1939年后到发沙大学做数学教授。他的 生主要研究拓扑学与集合论。 了 库拉托斯基于1954年率波兰数学家代表团对我国进行 学术访问,还送给了华罗庚一些波兰数学家写的数论函数 论文
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 11 注: (1) 库拉托斯基定理可以等价叙述为: 库拉托斯基定理:图G是非可平面的,当且仅当它含有 K5或K3,3同胚的子图。 (2) 库拉托斯基 (1896---1980) 波兰数学家。1913年开始 在苏格兰格拉斯哥大学学习工程学,1915年回到波兰发沙 大学转学数学,主攻拓扑学。1921年获博士学位。1930年 在利沃夫大学作数学教授期间,发现并证明了图论中的库 拉托斯基定理。1939年后到发沙大学做数学教授。他的一 生主要研究拓扑学与集合论。 库拉托斯基于1954年率波兰数学家代表团对我国进行了 学术访问,还送给了华罗庚一些波兰数学家写的数论函数 论文