
性质2行列式某行(列)元素的公因子可提到行列式符号之外:即ayaylay2anap2n....··::.::...AairMa2..Aain=元aiai?Win..::.!.:anianannan2annan2.或者说,以一数乘行列式的一行(列)就相当于用这个数乘此行列式kr,kc;推论行列式中某一行(列)为零,则行列式为零R区F32.4行列式的性质
§2.4 行列式的性质 行列式某行(列)元素的公因子可提到 行列式符号之外.即 11 12 11 12 1 1 1 2 1 2 1 2 1 2 n n i i in i i in n n nn n n nn a a a a a a a a a a a a a a a a a a = 推论 行列式中某一行(列)为零,则行列式为零. 性质2 或者说,以一数乘行列式的一行(列)就相当于 用这个数乘此行列式. i kr i kc
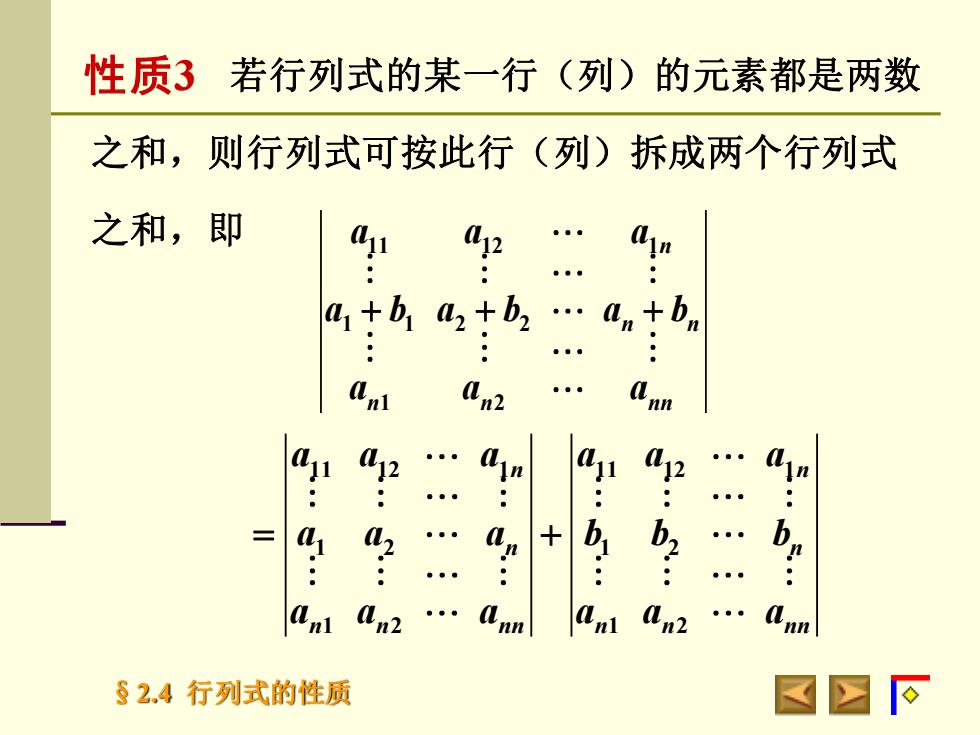
性质3若行列式的某一行(列)的元素都是两数之和,则行列式可按此行(列)拆成两个行列式之和,即ayiap2ayn.....+b,ai+b,a, +b,...a.-...anan2anna2aynay2::......"...b...十ananlannannan2an2下82.4行列式的性质
§2.4 行列式的性质 若行列式的某一行(列)的元素都是两数 11 12 1 11 12 1 1 2 1 2 1 2 1 2 n n n n n n nn n n nn a a a a a a a a a b b b a a a a a a = + 之和,则行列式可按此行(列)拆成两个行列式 之和,即 性质3 11 12 1 1 1 2 2 1 2 n n n n n nn a a a a b a b a b a a a + + +