
常见的连续性随机变量的分布 (1)均匀分布若X的df为 a<x<b 0, 其他 则称X服从区间(a,b)上的均匀分布或称 X服从参数为a,b的均匀分布.记作 X~U(a,b)
(1) 均匀分布 常见的连续性随机变量的分布 若 X 的 d.f. 为 = − 0, 其他 , 1 ( ) a x b f x b a 则称 X 服从区间( a , b)上的均匀分布或称 X ~ U(a,b) X 服从参数为 a , b的均匀分布. 记作

X的分布函数为 x<a, F=m- a≤x≤b: h-a X≥b
X 的分布函数为 − − = 1 , 0, b a x a x b a x b x a , , − = x F(x) f (t) dt
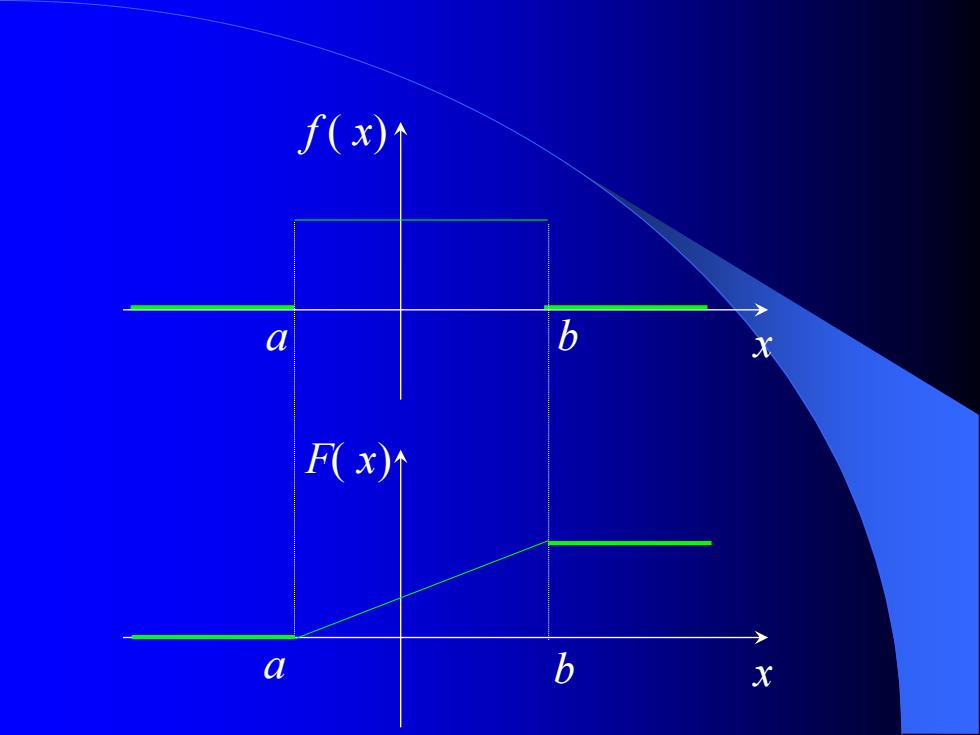
f(x) F(x)
x f ( x) a b x F( x) a b

V(c,d)E(a,b),P(c<X<d)=d dx= d-c b-a 即X落在(a,b)内任何长为dc的小区间的 概率与小区间的位置无关,只与其长度成正 比.这正是几何概型的情形 应用场合 进行大量数值计算时,若在小数点后第 k位进行四舍五入,则产生的误差可以看作 服从 -100 的水随机变量
(c,d) (a,b), x b a P c X d d 1 ( ) d c − = b a d c − − = 即 X 落在(a,b)内任何长为 d – c 的小区间的 概率与小区间的位置无关, 只与其长度成正 比. 这正是几何概型的情形. 进行大量数值计算时, 若在小数点后第 k 位进行四舍五入, 则产生的误差可以看作 服从 的 r.v. 随机变量 − −k −k U 10 2 1 10 , 2 1 应用场合

(2)指数分布 若X的dlf为 ,x>0 见>0为常数 其他 则称X服从参数为入的指数分布 记作X~E(2) X<0 X的分布函数为
(2) 指数分布 若 X 的d.f. 为 = − 0, 其他 , 0 ( ) e x f x x 则称 X 服从 参数为 的指数分布 记作 X ~ E() X 的分布函数为 − = − 1 , 0 0, 0 ( ) e x x F x x > 0 为常数