
解根据题意待检假设可设为 H:4≤0.8; H1:4>0.8 σ未知,故选检验统计量: T X-4 S/V16 ~T15) 查表得t.0s(15)=1.753,故拒绝域为 x-0.8 >1.7 3→x>0.8+1.75303 =0.94 s//n 4 现x=0.92<0.94 故接受原假设,即不能否定厂方断言
H0 : µ ≤ 0.8 ; H1 : µ > 0.8 σ 未知, 故选检验统计量: ~ (15) / 16 X T T S − µ = 查表得 t0.05(15) = 1.753, 故拒绝域为 0.8 1.753 / x s n − > ⇒ 0.32 0.8 1.753 0.94 4 x >+ = 现 x = < 0.92 0.94 故接受原假设, 即不能否定厂方断言. 解 根据题意待检假设可设为
2、关于o2的检验 x检验法 原假设 备择假设 检验统计量及其在 拒绝域 H H H为真时的分布 02=002 02≠002 x2≤g(m) ∑X- 或x2之X(m) 022002 02<002 z2≤X.(m ~x(n) (u己知) 02≤002 62>002 X2≥xa(n)
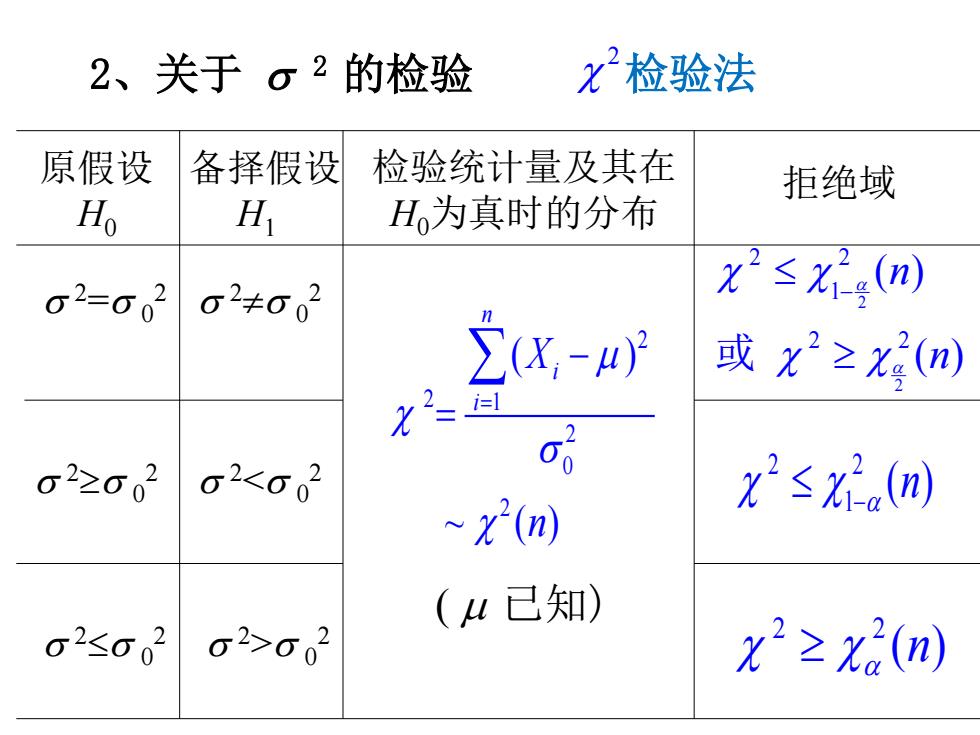
σ 2≤σ 0 2 σ 2>σ 0 2 2 2 ( ) n χ χα ≥ σ 2<σ 0 2 2 2 1 ( ) n α χ χ − σ ≤ 2≥σ 0 2 σ 2=σ 0 2 σ 2≠σ 0 2 原假设 H0 备择假设 H1 检验统计量及其在 H0为真时的分布 拒绝域 检验法 2 χ ( µ 已知) 2 2 1 2 0 2 ( ) ~ () n i i X n µ χ σ χ = − = ∑ 2 2 2 2 1 2 2 ( ) ( ) n n α α χ χ χ χ − ≤ 或 ≥ 2、关于 σ 2 的检验