其图形如图1-10所示。h(t在一阶系统中,时间常数是反映系统特性的重要参数,实际上它决定了一阶系统适用的频率范围:(1)当激励频率の远小于1/T时(约①),其A4()值接近于1(误差不超过2%),即输出、输入幅值几乎相等。(2)当激励频率の=时,4(一)=一号,而201g(方)-3dB,所以通常把当=处的频率称为系统的“转折频率”(在滤波器中称为截止频率)。(3)当激励频率の>(2~3)/t时,H()=1/jot,与之相应的微分方程式为(0)=I x(0)dt即输出和输入的积分成正比,系统相当于一个积分器。其中A(o)几乎与激励频率成反比,相位滞后90°。例 1-1已知某一阶系统的时间常数 t=6ms,试求相应于QT=1时的频率?若输入为此频率的正弦信号,则其实际输出的幅值误差是多少?解:因为t=1,故の=,则0=x1-rd/ -167ra/ 对应于OT=1的频率为-号- 167 ±=26.52元2元将QT=1代入式(1-33),得~0.707A(0) :V1+(to)2则输出的幅值误差为(1-0.707)×100%=29.3%。(二)二阶系统图1-11是弹簧---质量---阻尼系统和RLC电路,是两种典型的二阶测量系统。与一阶系统相比,二阶系统的特点是系统中有两个储能元件,输入、输出关系可用二阶微分方程来-11
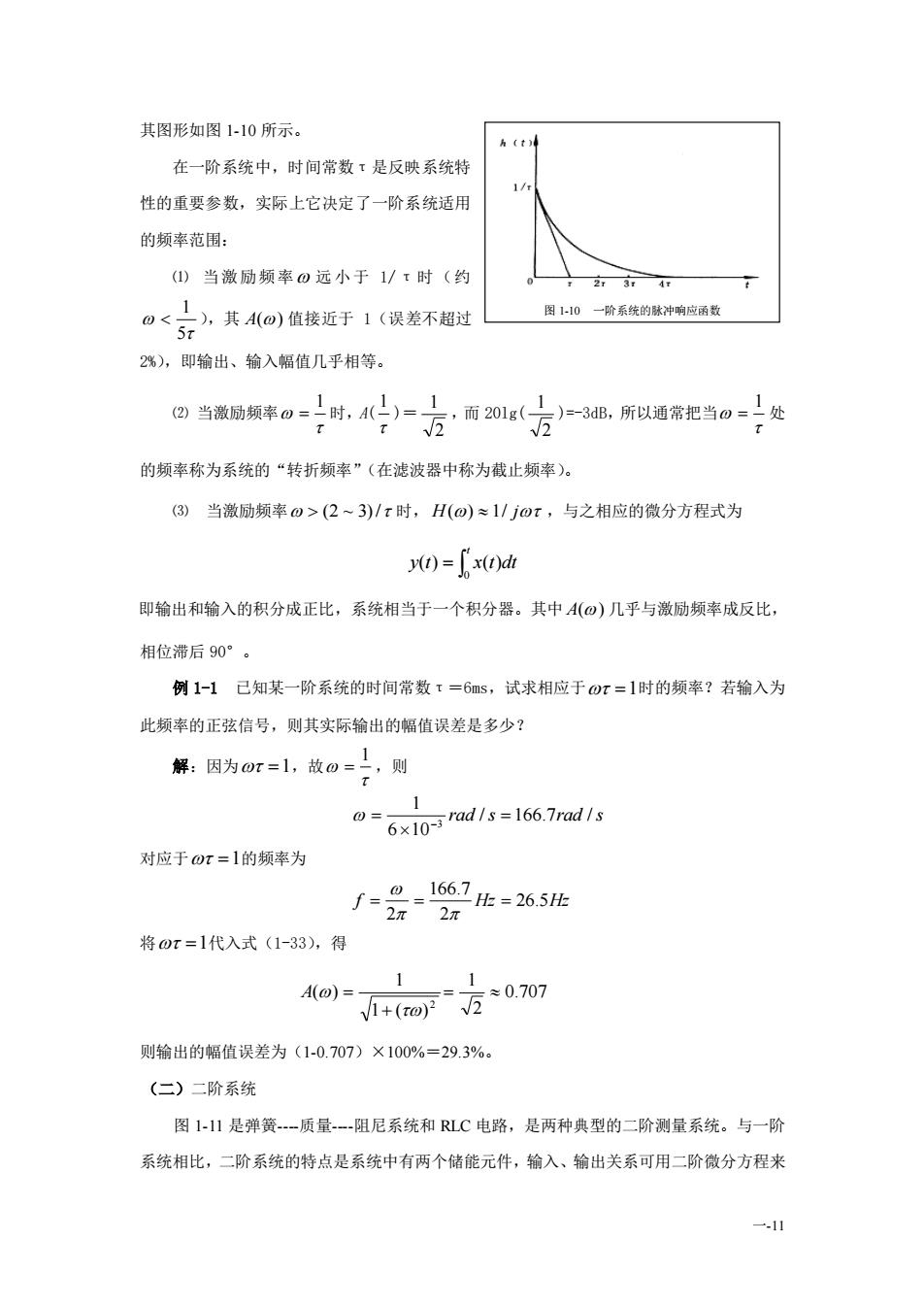
一-11 其图形如图 1-10 所示。 在一阶系统中,时间常数τ是反映系统特 性的重要参数,实际上它决定了一阶系统适用 的频率范围: ⑴ 当激励频率 远小于 1/τ时(约 5 1 ),其 A() 值接近于 1(误差不超过 2%),即输出、输入幅值几乎相等。 ⑵ 当激励频率 1 = 时,A( 1 )= 2 1 ,而 20lg( 2 1 )=-3dB,所以通常把当 1 = 处 的频率称为系统的“转折频率”(在滤波器中称为截止频率)。 ⑶ 当激励频率 (2 ~ 3)/ 时, H() 1/ j ,与之相应的微分方程式为 = t y t x t dt 0 ( ) ( ) 即输出和输入的积分成正比,系统相当于一个积分器。其中 A() 几乎与激励频率成反比, 相位滞后 90°。 例 1-1 已知某一阶系统的时间常数τ=6ms,试求相应于 =1 时的频率?若输入为 此频率的正弦信号,则其实际输出的幅值误差是多少? 解:因为 =1 ,故 1 = ,则 rad /s 166.7rad /s 6 10 1 3 = = − 对应于 =1 的频率为 f Hz 26.5Hz 2 166.7 2 = = = 将 =1 代入式(1-33),得 0.707 2 1 1 ( ) 1 ( ) 2 = + = A 则输出的幅值误差为(1-0.707)×100%=29.3%。 (二)二阶系统 图 1-11 是弹簧-质量-阻尼系统和 RLC 电路,是两种典型的二阶测量系统。与一阶 系统相比,二阶系统的特点是系统中有两个储能元件,输入、输出关系可用二阶微分方程来 图 1-10 一阶系统的脉冲响应函数
描述。类似于一阶系统,二阶系统微分方程的通式为d'yl +a, 0 + 0(0)=bx()(135)dtdt令测试系统的固有频率为:aoWn=a2测试系统的阻尼比系数为:f(c)a_ 2Jaod2测试系统的灵敏度为:20)S=5(b)ao图1-11二阶系统实例(a)弹策一质量一阻尼系统(b)RLC振荡电路则式(1-35)可改写成+250. 4+0:0)-Se:0(1-36)dt?ndt其中,对具体系统而言,S是一个常数。可令S=1,便得到归一化的二阶微分方程式,可作为研究二阶系统特性的标准式。由此可求得二阶系统的传递函数为02Y(s)H(s) =(1 37) X(s)s? +250,s+0)相应的频响函数H(o)=(1-38)[1-(-)1+ j25 %幅频特性和相频特性分别为(1-39)A(の) =[1-()P+4()-12
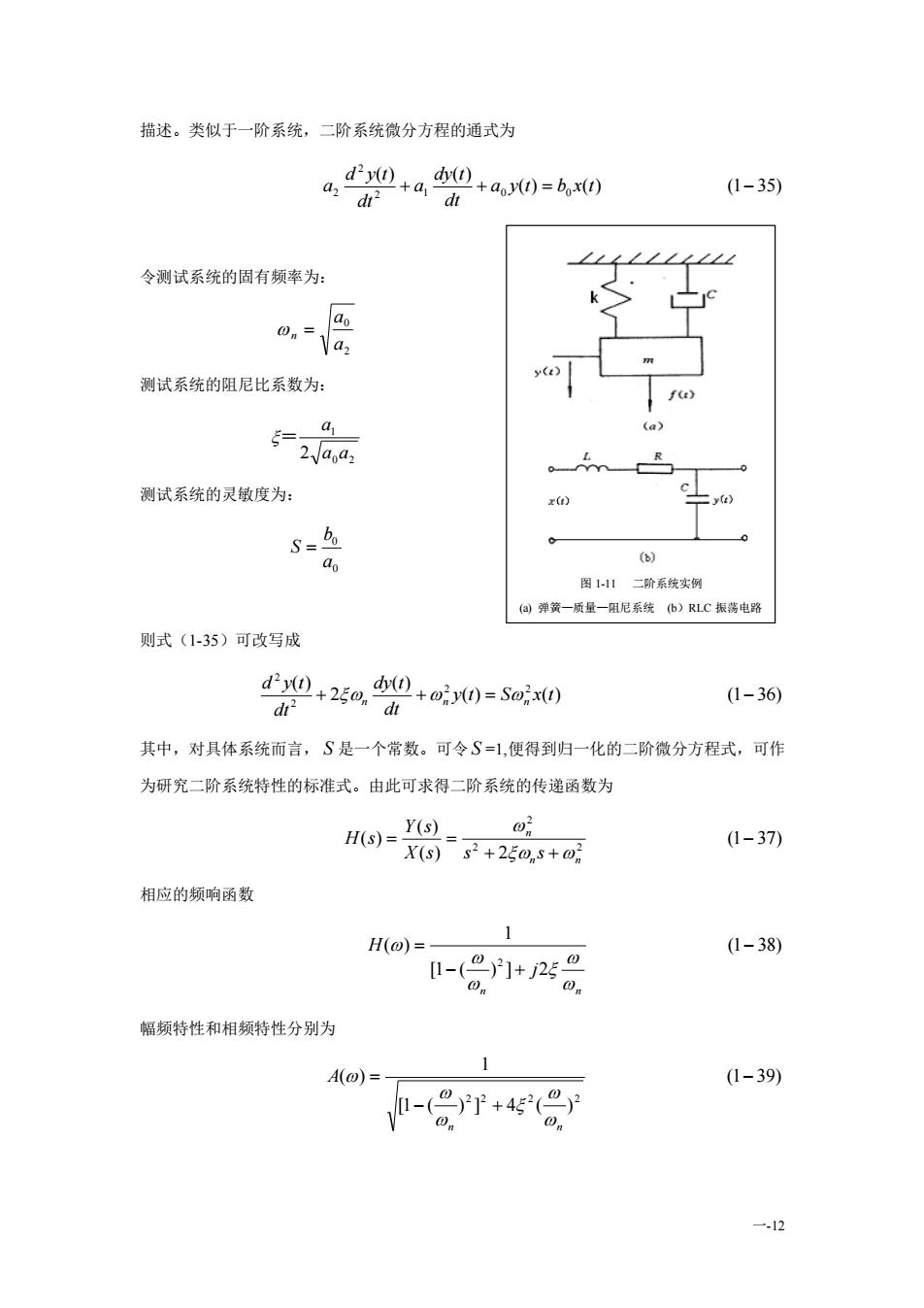
一-12 描述。类似于一阶系统,二阶系统微分方程的通式为 ( ) ( ) (1 35) ( ) ( ) 2 1 0 0 2 2 + + a y t = b x t − dt dy t a dt d y t a 令测试系统的固有频率为: 2 0 a a n = 测试系统的阻尼比系数为: 0 2 1 2 a a a = 测试系统的灵敏度为: 0 0 a b S = 则式(1-35)可改写成 ( ) ( ) (1 36) ( ) 2 ( ) 2 2 2 2 + + y t = S x t − dt dy t dt d y t n n n 其中,对具体系统而言, S 是一个常数。可令 S =1,便得到归一化的二阶微分方程式,可作 为研究二阶系统特性的标准式。由此可求得二阶系统的传递函数为 (1 37) ( ) 2 ( ) ( ) 2 2 2 − + + = = n n n X s s s Y s H s 相应的频响函数 (1 38) [1 ( ) ] 2 1 ( ) 2 − − + = n n j H 幅频特性和相频特性分别为 (1 39) [1 ( ) ] 4 ( ) 1 ( ) 2 2 2 2 − − + = n n A 图 1-11 二阶系统实例 (a) 弹簧—质量—阻尼系统 (b)RLC 振荡电路

25()(0) =-arctan -(1-40)1-()相应的幅频、相频特性曲线如图1-12所示。elo1图1-12二阶系统的幅频、相频特性曲线(a)幅频特性(6) 相频特性二阶系统的脉冲响应函数为0h(t) =Fe sin i-go,10<5<1(1-41)1-52其图形如图1-13所示。0.1图1-13阶系统的脉由式(1-41)和图(1-14)可知,二阶系统的频率特性受两个参数の,和三的共同影响。当阻尼三很大时(5>1),二阶系统的频率特性和一阶系统的频率特性比较接近,此时系统可近似为一阶系统。当很小时(0<《1)时,在の,处,系统响应幅值最大,即系统发生13
一-13 (1 40) 1 ( ) 2 ( ) ( ) arctan 2 − − = − n n 相应的幅频、相频特性曲线如图 1-12 所示。 二阶系统的脉冲响应函数为 sin 1 0 1 (1 41) 1 ( ) 2 2 − − − = − h t e t n n t n 其图形如图 1-13 所示。 由式(1-41)和图(1-14)可知,二阶系统的频率特性受两个参数 n 和 的共同影响。 当阻尼 很大时( >1),二阶系统的频率特性和一阶系统的频率特性比较接近,此时系统 可近似为一阶系统。当 很小时(0< <<1)时,在 n 处,系统响应幅值最大,即系统发生 图 1-13 二阶系统的脉冲响应函数 图 1-12 二阶系统的幅频、相频特性曲线 (a)幅频特性 (b) 相频特性