
第三节测量装置的动态特性当被测参数随时间变化时,测量装置处于动态测量状态。则动态特性指动态测量时,测量装置的输出量与被测输入量之间随时间变化的函数关系。在动态测量情况下,测量装置的输入、输出关系除与静态特性有关外,还受动态特性影响。且动态特性不仅取决于测量装置的结构,而且还与输入信号有关。所以描述测量装置的动态特性,实质上就是建立输入信号、输出信号和测量装置三者之间的关系。通常用测量装置的传递函数、频率相应函数和脉冲相应函数来描述测量装置的动态传递特性。三者从不同角度表示出测量装置的动态特性,它们之间既互相联系又各有其特点。一、传递函数若测量装置处于零初始条件,即当1≤0时,输入信号x()、输出信号y()及其各阶导数均为零,则对式(1-1)进行拉普拉斯变换,可得:(a,s" +a-s"- +.+ais+ao)Y(s)=(b.s" +b.-ism- +..+b,s+bo)X(s)则Y(s) _ bms"+b-s"++bys+bo(1-14)X()a,sa-".a+a式中an、an-1、*、ar、ao和bm、bm-1、、bi、bo均是由测量装置确定的常数。式(1-14)是测量装置传递特性的一种表达式。为此,将初始条件为零时,输出信号和输入信号的拉普拉斯变换之比称为测量装置的传递函数 H(s),即O-10(1-15) Y(s)= I, y(0)e"dy(t)x(tX(s) = x(0)e" dtX(s)H(a)Y(s)式中Y(s)——输出信号y()的拉普拉斯变换;输入输出图 1-4 测试系统、输入与输出三者关系X(s)——输入信号x()的拉普拉斯变换;——拉普拉斯算子,S=α+joα和o皆为实变量)(α>0,--6
一-6 第三节 测量装置的动态特性 当被测参数随时间变化时,测量装置处于动态测量状态。则动态特性指动态测量时,测 量装置的输出量与被测输入量之间随时间变化的函数关系。在动态测量情况下,测量装置的 输入、输出关系除与静态特性有关外,还受动态特性影响。且动态特性不仅取决于测量装置 的结构,而且还与输入信号有关。所以描述测量装置的动态特性,实质上就是建立输入信号、 输出信号和测量装置三者之间的关系。通常用测量装置的传递函数、频率相应函数和脉冲相 应函数来描述测量装置的动态传递特性。三者从不同角度表示出测量装置的动态特性,它们 之间既互相联系又各有其特点。 一、传递函数 若测量装置处于零初始条件,即当 t ≤0 时,输入信号 x(t) 、输出信号 y(t) 及其各阶导 数均为零,则对式(1-1)进行拉普拉斯变换,可得: ( ) ( ) ( ) ( ) 1 0 1 1 1 0 1 1 b s b s b s b X s a s a s a s a Y s m m m m n n n n = + + + + + + + + − − − − 则 (1 14) ( ) ( ) 1 0 1 1 1 0 1 1 − + + + + + + + + = − − − − a s a s a s a b s b s b s b X s Y s n n n n m m m m 式中 an、an-1、.、a1、a0 和 bm、bm-1、.、b1、b0 均是由测量装置确定的常数。式(1-14) 是测量装置传递特性的一种表达式。为此,将初始条件为零时,输出信号和输入信号的拉普 拉斯变换之比称为测量装置的传递函数 H(s) ,即 (1 15) ( ) ( ) ( ) = − X s Y s H s − − = = 0 0 ( ) ( ) ( ) ( ) X s x t e dt Y s y t e dt st st 式中 Y(s)——输出信号 y(t)的拉普拉斯变换; X(s)——输入信号 x(t)的拉普拉斯变换; s——拉普拉斯算子, s = + j ( 0, 和皆为实变量) 输入 输出 图 1-4 测试系统、输入与输出三者关系 x(t) X(s) Y(s) y(t)

传递函数表示测量装置的输入信号与输出信号之间在复数域内的关系(图1-4)),它有如下特点:1、H(s)描述系统本身的固有特性,与输入信号x()的类型无关。x()不同时,y(t)也不同,但二者拉普拉斯变换的比值H(s)保持不变。2、H(s)反映测量装置的传输、转换和响应特性,与具体物理结构无关。同一形式的传递函数可以表征具有相同传输特性的不同物理系统2、H(s)起传递作用,只要知道X(s)、Y(s)、H(s)三者中的任意两个,则可以很方便地求出第三者。二、频率响应函数若能在频域中研究测量装置对任意输入的响应,则将有可能简化研究过程。为此,将s-j@代入(1-14),就可得到Y(jo)_ b.(Go)*+b.(jo)++b(jo)+b.(116)X(jo) .,(jo)+.(jo)*+,(o)+.o对比复数域传递函数的定义,可得测量装置在频域的传递函数,称为频率响应函数(简称频响函数),即- (1-17)式中Ya)——输出信号y(的傅氏变换,Y(jo)=y()e-adt;XG)——输出信号x(0的傅氏变换;X(jo)=x(1)e-adt用频响函数来描述系统的最大优点是它可以通过实验求得。即依次用不同频率の,的简谐信号去激励被测装置,同时测得激励(输入)和装置的稳态输出幅值%i、6和相位差9。Yoi这样对于某个の,便有一=4和9,全部的4-0和9-0(=1,2),便可表To达测量装置的频率响应函数。三、脉冲响应函数若输入为单位脉冲8()(图1-5a),即x(0=8(t),则其拉氏变换X(s)=L[6(1)=1。根据式(1-15),测量装置的相应输出将是Y(s)=H(s)X(s)=H(s),其时域描述可以通过对 Y(s)-7
一-7 传递函数表示测量装置的输入信号与输出信号之间在复数域内的关系(图 1-4),它有 如下特点: 1、H(s)描述系统本身的固有特性,与输入信号 x(t) 的类型无关。x(t)不同时,y(t)也不 同,但二者拉普拉斯变换的比值 H(s)保持不变。 2、H(s)反映测量装置的传输、转换和响应特性,与具体物理结构无关。同一形式的传 递函数可以表征具有相同传输特性的不同物理系统。 2、H(s)起传递作用,只要知道 X(s)、Y(s)、H(s)三者中的任意两个,则可以很方便地求 出第三者。 二、频率响应函数 若能在频域中研究测量装置对任意输入的响应,则将有可能简化研究过程。为此,将 s=jω代入(1-14),就可得到 (1 16) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 1 0 1 1 1 0 1 1 − + + + + + + + + = − − − − a j a j a j a b j b j b j b X j Y j n n n n m m m m 对比复数域传递函数的定义,可得测量装置在频域的传递函数,称为频率响应函数(简称频 响函数),即 (1 17) ( ) ( ) ( ) = − X j Y j H j 式中 Y(jω)——输出信号 y(t)的傅氏变换, − = 0 Y( j ) y(t)e dt jt ; X(jω)——输出信号 x(t)的傅氏变换; − = 0 X( j ) x(t)e dt jt 用频响函数来描述系统的最大优点是它可以通过实验求得。即依次用不同频率 i 的简 谐信号去激励被测装置,同时测得激励(输入)和装置的稳态输出幅值 X0i、Y0i 和相位差 i 。 这样对于某个 i ,便有一组 i i i A X Y = 0 0 和 i ,全部的 Ai −i 和 i −i (i=1,2,.),便可表 达测量装置的频率响应函数。 三、脉冲响应函数 若输入为单位脉冲δ(t)(图 1-5a),即 x(t)= δ(t),则其拉氏变换 X(s) = L (t) =1。 根据式(1-15),测量装置的相应输出将是 Y(s)=H(s)X(s)=H(s),其时域描述可以通过对 Y(s)

的拉普拉斯反变换得到,即(0) = L-[H(s)] = h(0) (118)h(t)称为测量装置的脉冲响应函数或权函数(图1-5b)。脉冲响应函数可作为系统特性的时域描述。综上所述,系统特性在时域可用脉冲响应函数h()来描述,在频域可用频率响应函数 HG)来描述,在复数域可-5单位脉冲和脉冲响应函用传递函数 H(s)来描述。三者的关系也是一对应的。脉冲响应函数 h()和传递函数 H(s)是一个拉普拉斯变换对,h()与频率响应函数H()是一个傅氏变换对。四、环节的串联和并联如果测试系统是由两个环节串联而成(图1-6),它们的传递函数分别为Hi(s)和 H(s),则该串联系统的传递函数为_ Y() - ZY = H(S)H(s)H(s)=(1-19) X(s)X(s) Z(s)可以推出,若测试系统有多个环节串联而成,其总的传递函数为H(s)= H(s)H,(s)..H,(s)- IIH(s)(120)如果测试系统有两个环节并联而成(图1-7),它们的传递函数分别为H,(s)和H,(s),则该并联系统的传递函数为--+-H()+H()H(s) =(1-21)X()" X(s) +X(s)由此可推出,多个环节并联而成的测试系统,总的传递函数为H(s)= H;(s)+H,(s)+H,(s)=2h,(s)(122) 同样,令s-jo代入式(1-20)和式(1-22)得到n个环节串联系统频响函数为H(0)=IIH(o)(I-23) -8
一-8 的拉普拉斯反变换得到,即 ( ) [ ( )] ( ) (1 18) 1 = = − − y t L H s h t h(t)称为测量装置的脉冲响应函数或权 函数(图 1-5b)。脉冲响应函数可作为系 统特性的时域描述。 综上所述,系统特性在时域可用脉 冲响应函数 h(t)来描述,在频域可用频 率响应函数 H(jω)来描述,在复数域可 用传递函数 H(s)来描述。三者的关系也是一一对应的。脉冲响应函数 h(t)和传递函数 H(s) 是一个拉普拉斯变换对,h(t)与频率响应函数 H(ω)是一个傅氏变换对。 四、环节的串联和并联 如果测试系统是由两个环节串联而成(图 1-6),它们的传递函数分别为 H1(s)和 H2(s), 则该串联系统的传递函数为 ( ) ( ) (1 19) ( ) ( ) ( ) ( ) ( ) ( ) ( ) = = = H1 s H2 s − Z s Y s X s Z s X s Y s H s 可以推出,若测试系统有多个环节串联而成,其总的传递函数为 ( ) ( ) ( ) ( ) ( ) (1 20) 1 = 1 2 = − = n i n i H s H s H s H s H s 如果测试系统有两个环节并联而成(图 1-7),它们的传递函数分别为 ( ) 1 H s 和 ( ) 2 H s , 则该并联系统的传递函数为 ( ) ( ) (1 21) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 1 2 1 2 = = + = H s + H s − X s Y s X s Y s X s Y s H s 由此可推出,多个环节并联而成的测试系统,总的传递函数为 ( ) ( ) ( ) ( ) ( ) (1 22) 1 = 1 + 2 + + = − = n i n i H s H s H s H s H s 同样,令 s=jω代入式(1-20)和式(1-22)得到 n 个环节串联系统频响函数为 ( ) ( ) (1 23) 1 = − = n i H Hi 1-5 单位脉冲和脉冲响应函数
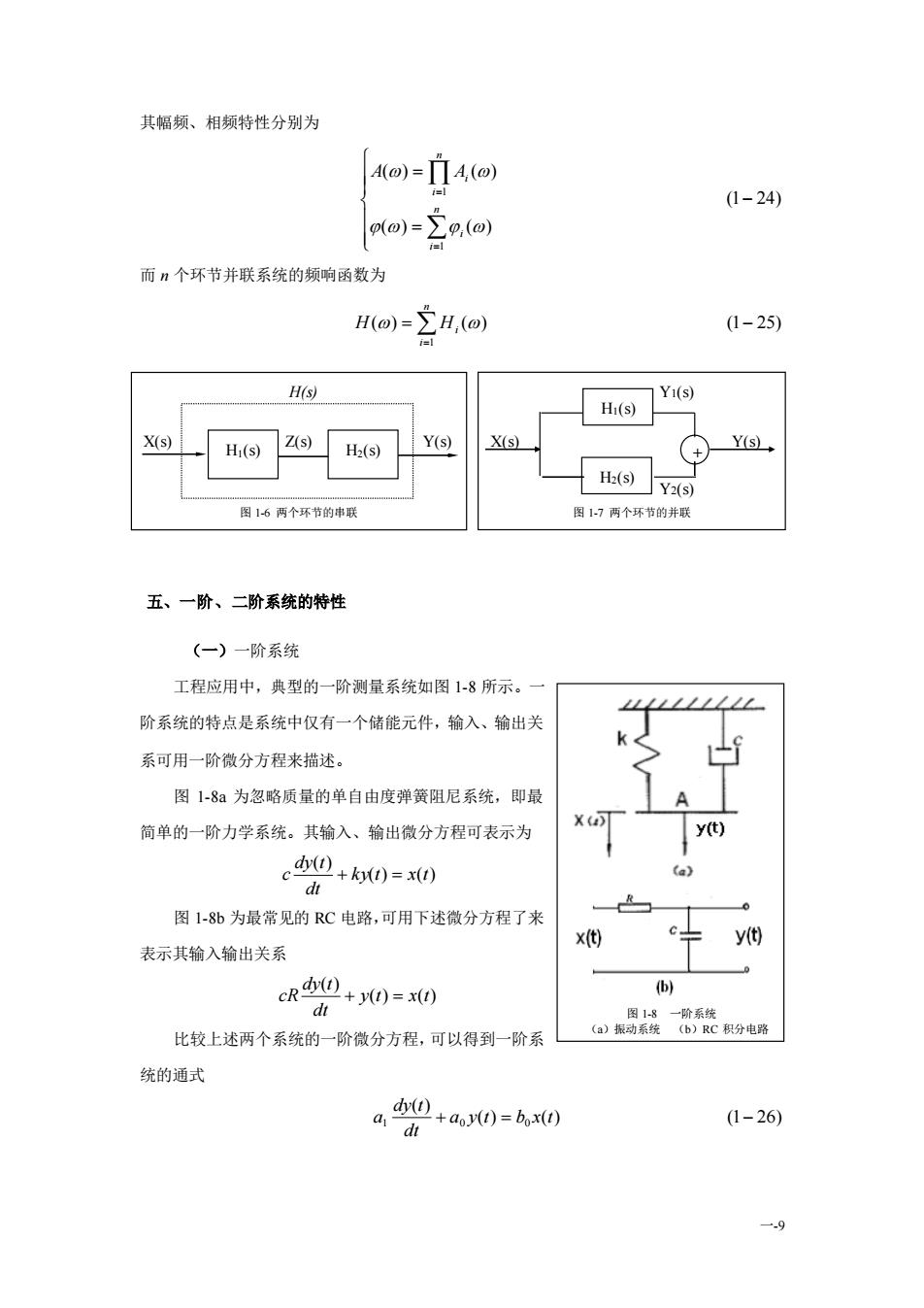
其幅频、相频特性分别为A(0)=I/4(0)(1-24)Zg,(0)而n个环节并联系统的频响函数为H(0)=ZH,(o)(125)H(s)Y1(s)Hi(s)X(s)(S)H(s)X(s)Hi(s)H2(s)Y2(S)图1-6两个环节的串联图1-7两个环节的并联五、一阶、二阶系统的特性(一)一阶系统工程应用中,典型的一阶测量系统如图1-8所示阶系统的特点是系统中仅有一个储能元件,输入、输出关k<系可用一阶微分方程来描述。图1-8a为忽略质量的单自由度弹簧阻尼系统,即最X4[y(t)简单的一阶力学系统。其输入、输出微分方程可表示为d() + ky(0)= x()(a)图1-8b为最常见的RC电路,可用下述微分方程了来十y(t)x(t)表示其输入输出关系cR ≤ + () =x)(b)1() 显联线一的系能 积分电路比较上述两个系统的一阶微分方程,可以得到一阶系统的通式 + ao)()= box()( 26) 1dt
一-9 其幅频、相频特性分别为 (1 24) ( ) ( ) ( ) ( ) 1 1 − = = = = n i i n i A Ai 而 n 个环节并联系统的频响函数为 ( ) ( ) (1 25) 1 = − = n i H Hi 五、一阶、二阶系统的特性 (一)一阶系统 工程应用中,典型的一阶测量系统如图 1-8 所示。一 阶系统的特点是系统中仅有一个储能元件,输入、输出关 系可用一阶微分方程来描述。 图 1-8a 为忽略质量的单自由度弹簧阻尼系统,即最 简单的一阶力学系统。其输入、输出微分方程可表示为 ( ) ( ) ( ) ky t x t dt dy t c + = 图 1-8b 为最常见的 RC 电路,可用下述微分方程了来 表示其输入输出关系 ( ) ( ) ( ) y t x t dt dy t cR + = 比较上述两个系统的一阶微分方程,可以得到一阶系 统的通式 ( ) ( ) (1 26) ( ) 1 + a0 y t = b0 x t − dt dy t a H(s) X(s) Z(s) Y(s) 图 1-6 两个环节的串联 图 1-7 两个环节串连 H1(s) H2(s) Y1(s) X(s) Y(s) Y2(s) 图 1-7 两个环节的并联 H1(s) H2(s) + 图 1-8 一阶系统 (a)振动系统 (b)RC 积分电路
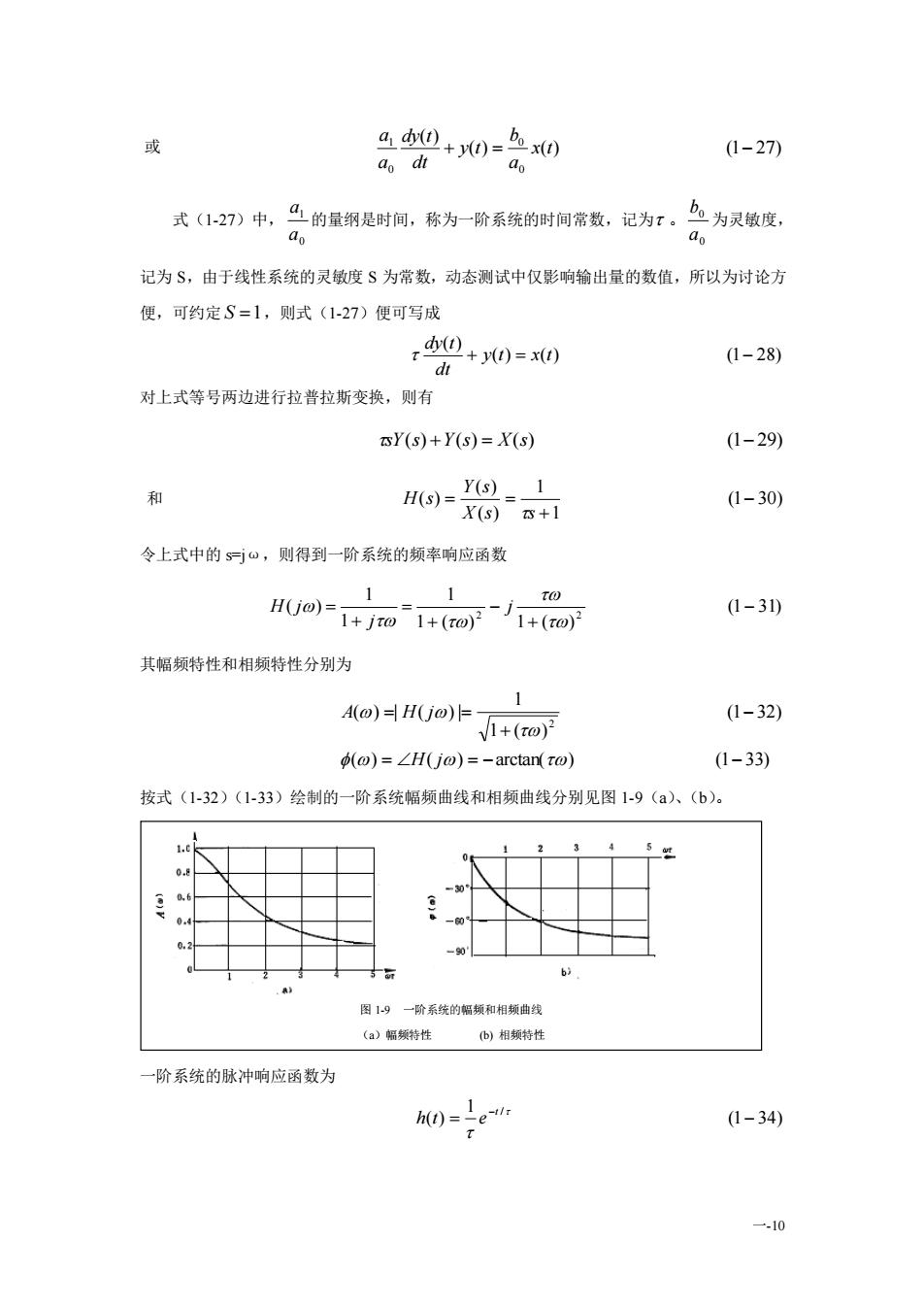
+ (0)=x()或(127)aodtbo为灵敏度,"的量纲是时间,称为一阶系统的时间常数,记为T。式(1-27)中记为S,由于线性系统的灵敏度s为常数,动态测试中仅影响输出量的数值,所以为讨论方便,可约定S=1,则式(1-27)便可写成 + y(0)= x()(28)dt对上式等号两边进行拉普拉斯变换,则有Y(s)+Y(s) = X(s)(1-29)H(s)= Y() _和(130)X(s)$+1令上式中的sjo,则得到一阶系统的频率响应函数TOH(jo)=(1-31)+ jto1+(to)?1+(t0)2其幅频特性和相频特性分别为(1 32) A(o)= H(jo)=-/1+(to)?(1-33)(o) = ZH(jo) = -arctan( to)按式(1-32)(1-33)绘制的一阶系统幅频曲线和相频曲线分别见图1-9(a)、(b)。:图1-9一阶系统的幅频和相频曲线(a)幅频特性(b)相频特性一阶系统的脉冲响应函数为ho -1e":(134)--10
一-10 或 ( ) ( ) (1 27) ( ) 0 0 0 1 + = x t − a b y t dt dy t a a 式(1-27)中, 0 1 a a 的量纲是时间,称为一阶系统的时间常数,记为 。 0 0 a b 为灵敏度, 记为 S,由于线性系统的灵敏度 S 为常数,动态测试中仅影响输出量的数值,所以为讨论方 便,可约定 S =1 ,则式(1-27)便可写成 ( ) ( ) (1 28) ( ) + y t = x t − dt dy t 对上式等号两边进行拉普拉斯变换,则有 sY(s) +Y(s) = X(s) (1− 29) 和 (1 30) 1 1 ( ) ( ) ( ) − + = = X s s Y s H s 令上式中的 s=jω,则得到一阶系统的频率响应函数 (1 31) 1 ( ) 1 ( ) 1 1 1 ( ) 2 2 − + − + = + = j j H j 其幅频特性和相频特性分别为 ( ) ( ) arctan( ) (1 33) (1 32) 1 ( ) 1 ( ) | ( ) | 2 = = − − − + = = H j A H j 按式(1-32)(1-33)绘制的一阶系统幅频曲线和相频曲线分别见图 1-9(a)、(b)。 一阶系统的脉冲响应函数为 (1 34) 1 ( ) / = − − t h t e 图 1-9 一阶系统的幅频和相频曲线 (a)幅频特性 (b) 相频特性