
第六章系统的性能与校正 讲授内容 6.1系统的性能指标 系统性能指标,按其类型可分为: (1)时域性能指标,它包括瞬态性能指标和稳态性能指标。其 中,瞬态性能指标一般是在单位阶跃输入下,由输出的过渡过程 所给出的,实质上是由瞬态响应所决定的,它主要包括延迟时间 14、上升时间1,、峰值时间1。、最大超调量或最大百分比超调量M 及调整时间(或过渡过程时间)·,等稳态性能指标主要指稳态 误差。 (2)频域性能指标,主要包括相位裕度y、幅值裕度K,、复 现频率0m、复现带宽0~0m、截止频率o,和截止带宽0~0等。 必须注意,系统频域性能指标与时域性能指标间存在一定的 关系,如峰值时间1,和调整时间1,都与系统的带宽有关:系统的 带宽越大,则系统响应的快速性就越好。 (3)综合性能指标(误差准则)是系统性能的综合测度。它们 是系统误差0)的某个函数的积分。在系统参数取最优值时,这 些指标将取极值,从而可以通过选择适当的参数得到综合性能指 标最优的系统。主要有以下三种: (a)误差积分性能指标:I=()d,适用于无超调系统。 (b)误差平方积分性能指标:1=e(u)d,适用于有超调系 统,其特点是,重视大的误差,忽略小的误差。根据这个指标设
第六章 系统的性能与校正 讲授内容 6.1 系统的性能指标 系统性能指标,按其类型可分为: (1)时域性能指标,它包括瞬态性能指标和稳态性能指标。其 中 ,瞬态性能指标一般是在单 位阶跃输入下,由输出的过渡过程 所给出的,实质上是由瞬态响应所决 定的,它主要包括延迟时间 、上升时间 、峰值时间 、最大超调量或最大百分比超调量 及调整时间 (或过渡过程时间) 等 ; 稳态性能指标主要指稳态 误差。 d t r t p t M p s t ( 2 )频域性能指标,主要包括相位裕度 γ 、幅值裕度 、 复 现频率 K g ω m、复现带宽 0 ~ω m、截止频率 ω b 和截止带宽 0 ~ω b 等。 必须注意,系统频域性能指标与时域性能指标间存在一定的 关系,如峰值时间 和调整时间 都与系统的带宽有关:系统的 带宽越大,则系统响应的快速性就越好。 p t s t (3)综合性能指标(误差准则)是系统性能的综合测度。它们 是系统误差 的某个函数的积分。在系统参数取最优值时,这 些指标将取极值,从而可以通过选择适当的参数得到综合性能指 标最优的系统。主要有以下三种: e(t) (a)误差积分性能指标: ,适用于无超调系统。 ∫ ∞ = 0 I e(t)dt ( b )误差平方积分性能指标: ,适用于有超调系 统 ,其特点是,重视大的误差,忽略小的误差。根据这个指标设 ∫ ∞ = 0 2 I e (t )dt

计的系统,能使大的误差迅速减小,但系统容易产生振荡。 (c)广义误差平方积分性能指标:1=[e2)+ae2()d,其特 点是不容许大的动态误差和大的误差变化率长期存在。根据这个 指标设计的系统,过渡过程结束快,而且其变化也比较平稳。 6.2系统的校正 一、校正的概念 所谓的校正(或称补偿),就是指在系统中增加新的环节, 以改善系统性能的方法。 二、校正的分类 校正方案:确定所采用的校正环节及其在系统中的位置,两 者合称为校正方案。线性定常系统的常用校正方案有: 增益调整 相位超前校正 串联校正 相位想潘后等收正 PD调节 并联校正 反馈校正 顺馈校正 6.3无源校正 串联校正可以分为无源校正和有源校正,其中无源校正包括 增益调整、相位超前校正、相位滞后校正以及相位滞后一一超前 校正等四种方式。由于单纯采用增益调整,不能同时保证系统的 稳定性和系统稳态精度都得到改善,往往在提高系统的稳定性的 同时,降低了系统响应的准确性,或者相反。因此,一般不采用 单纯的增益调整
计的系统,能使大的误差迅速减小,但系统容易产生振荡。 (c)广义误差平方积分性能指标: ,其 特 点是不容许大的动态误差和大的误差变化率长期存在。根据这个 指标设计的系统,过渡过程结束快,而且其变化也比较平稳。 ∫ ∞ = + 0 2 2 I [ e (t ) αe& (t )]dt 6.2 系统的校正 一、校正的概念 所谓的校正(或称补偿),就是指在系统中增加新的环 节 , 以改善系统性能的方法。 二、校正的分类 校正方案: 确定所采用的校正环节及其在系统中的位置, 两 者合称为校正方案。线性定常系统的常用校正方案有: ⎪ ⎪ ⎪ ⎪ ⎩ ⎪ ⎪ ⎪ ⎪ ⎨ ⎧ ⎩ ⎨ ⎧ ⎪ ⎪ ⎪ ⎩ ⎪ ⎪ ⎪ ⎨ ⎧ 顺馈校正 反馈 正 并联校正 调节 相位超前 滞后校正 相位滞后校正 相位超前校正 增益调整 串联校正 校 PID — — 6.3 无源校正 串联校正可以分为无源校正和有源校正,其中无源校正包括 增益调整、相位超前校正、相位滞后校正以及相位滞后——超前 校正等四种方式。由于单纯采用增益调整,不能同时保证系统的 稳定性和系统稳态精度都得到改善,往往在提高系统的稳定性的 同时,降低了系统响应的准确性,或者相反。因此,一般不采用 单纯的增益调整

一、相位超前校正 1.相位超前校正环节 相位超前环节的传递函数可用下式表示 G) (6.3.1) 式中,a<1,T为常数。 此相位超前环节的频率特性为:G(U)=a (T)+1) (iaTo+l 其中,相频特性为 ZG.(jo)=arctanTo-arctanaT@>0. 可见相位超前。它的幅频特性为: K.Vo)-aMToy+i (aTo)2+1 将G(Uo)分为实部u和虚部v,可得 Q+a) 图6.3.1 可见,G.Uo)的Nyquist轨迹是一个过点(1,j0),半径为1-), 圆心为片1+a,j0的半圆。又由于相角∠G。Uo)是正的,故G.o)轨 迹是其中的上半圆,如图6.3.1所示。 若此环节的最大相位超前角为p,则由 (6.3.2) 可知,当α减小时,p增大,如图63.2所示。从图中还可以看 出,随着频率o的减小,幅值G(@减小,所以,超前环节相当 于高通滤波器。 图6.3.3是相位超前环节Go=am+出的B0de图。其中频 (ja@+1
一、相位超前校正 1.相位超前校正环节 相位超前环节的传递函数可用下式表示 ( 1) ( 1) ( ) + + = Ts Ts G s c α α , ( 6.3.1) 式中, α < 1, T 为常数。 此相位超前环节的频率特性为: ( 1) ( 1) ( ) + + = α ω ω ω α j T jT G j c 其中,相频特性为 ∠Gc ( jω) = arctanTω − arctanαTω > 0。 可见相位超前。它的幅频特性为: ( ) 1 ( ) 1 ( ) 2 2 + + = α ω ω ω α T T G j c 将 G ( jω) c 分为实部 u 和虚部 v ,可得 2 2 2 2 1 2 1 ( u ) v ( ) α −α + = + − , 图 6.3.1 可 见 ,Gc ( jω) 的 Nyquist 轨迹是一个过点( 1,j0),半径为 (1 ) 2 1 −α , 圆心为 (1 ), 0] 2 1 [ +α j 的半圆。又由于相角 G ( jω) ∠ c 是正的,故 G ( jω) c 轨 迹是其中的上半圆,如图 6.3.1 所示。 若此环节的最大相位超前角为 ϕ m ,则由 α α ϕ + − = 1 1 sin m ( 6.3.2) 可知,当 α 减小时, ϕ m 增大,如图 6.3.2 所示。从图中还可以看 出 , 随着频率 ω 的减小, 幅 值 G ( jω) c 减小, 所以, 超前环节相当 于高通滤波器。 图 6.3.3 是相位超前环节 ( j T ) ( jT ) G ( j ) c 1 1 + + = α ω ω ω α 的 Bode 图。其中频
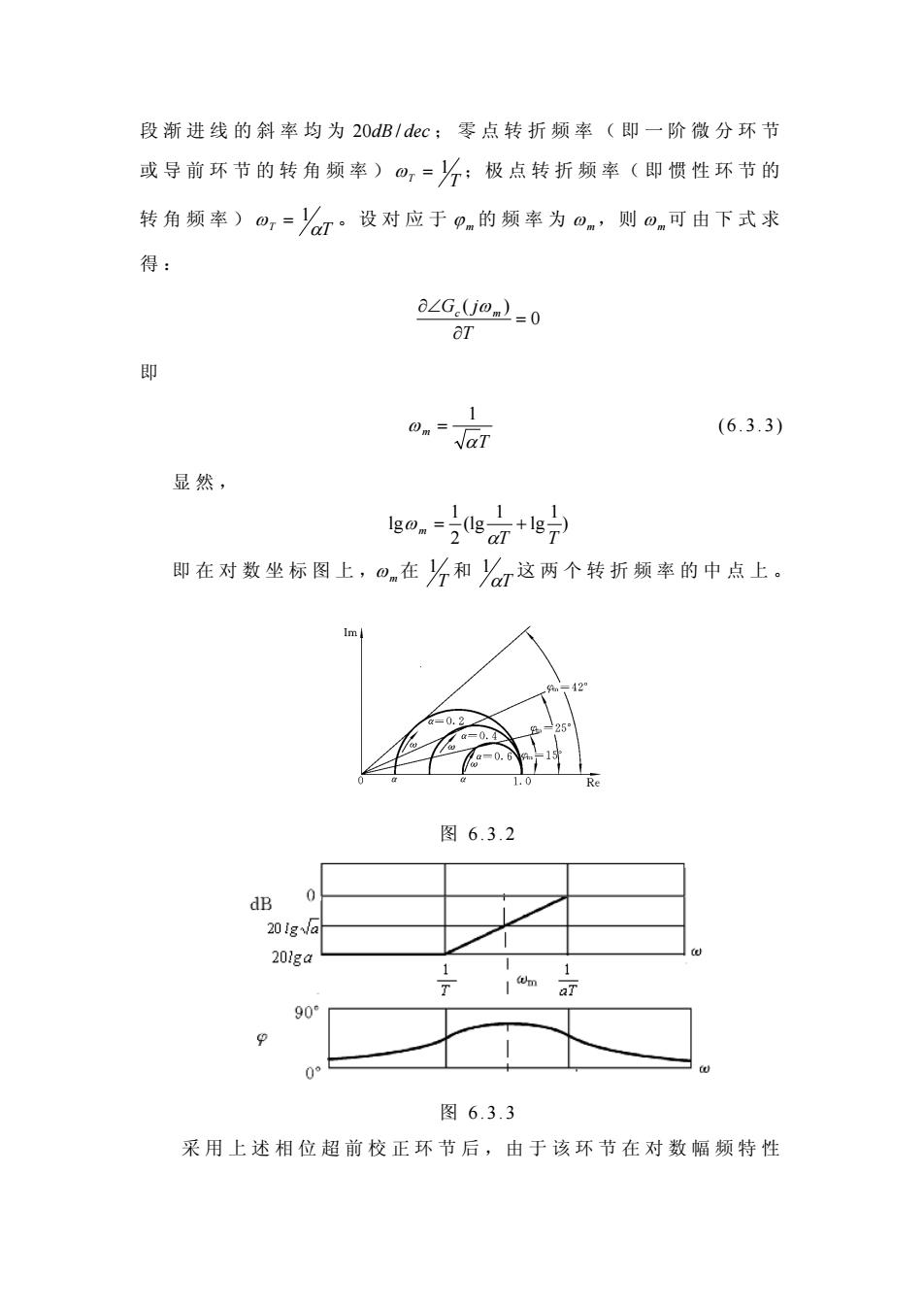
段渐进线的斜率均为20dB/dec;零点转折频率(即一阶微分环节 或导前环节的转角频率),=人:极点转折频率(即惯性环节的 转角频率),=么7·设对应于的频率为日,则a可由下式求 得: OLG.(jo)=0 OT 即 o.-JaT (6.3.3) 显然, go,=g7+lg宁 即在对数坐标图上,在和这两个转折频率的中点上。 m 图6.3.2 dB 0 201ga 90 图6.3.3 采用上述相位超前校正环节后,由于该环节在对数幅频特性
段渐进线的斜率均为 ;零点转折频率(即一阶微分环节 或导前环节的转角频率) 20dB / dec T T ω = 1 ;极点转折频率(即惯性环节的 转角频率) T αT ω = 1 。设对应于 ϕ m 的频率为 ω m,则 ω m可由下式求 得 : 0 ( ) = ∂ ∂∠ T G j c ω m 即 T m α ω 1 = ( 6.3.3) 显然, ) 1 lg 1 (lg 2 1 lg T T m = + α ω 即在对数坐标图上,ω m在 T 1 和 αT 1 这两个转折频率的中点上。 图 6.3.2 图 6.3.3 采用上述相位超前校正环节后,由于该环节在对数幅频特性

上有20dB/dec段存在,故加大了系统的剪切频率o。、谐振频率o,与 截止频率,其结果是加大了系统的带宽,加快了系统的响应速 度:又由于相位超前,还可能加大相位裕度,其结果是增加了系 统的相对稳定性。 2.采用Bode图进行相位超前校正 采用相位超前校正的一般设计步骤为: (1)根据系统稳态误差的要求,确定系统的开环增益K: (2)在已确定K值的条件下,计算未校正系统的相位裕度: (3)根据指标的要求,确定在系统中需要增加的相角超前量 Put (4)由式(6.3.2)确定α值,然后根据式(6.3.3)确定最大 超前角对应的频率o处的对数幅频特性值L.,即 L.=20g1+T@ 1+j。在未校正系统的对数幅频特好 1+jaTo -20lg+j小a 上找到幅值等于-L.点所对应的频率,该频率即为校正后系统新 的剪切频率⊙,同时也是所选超前网络的o,在此频率上超前网 络将产生最大超前相角值m;根据om确定T和aT: (5)确定超前校正环节的转折频率on=片,on=片a) (6)验算。 3.相位超前校正的特点 (1)相位超前校正主要对未校正系统在中频段的特性进行校 正。以确保校正后系统具有较高的相位裕度及中频段斜率等于 -20dB/dec。 (2)超前校正可以提高系统响应的快速性。相位超前校正环 节校正使系统截止频率增大,提高系统的响应速度。但随着带宽
上 有 20dB / dec 段存在,故加大了系统的剪切频率 ωc、谐振频率 ω r 与 截止频率 ωb ,其结果是加大了系统的带宽,加快了系统的响应速 度 ;又由于相位超前,还可能加大相位裕度,其结果是增加了系 统的相对稳定性。 2.采用 Bode 图进行相位超前校正 采用相位超前校正的一般设计步骤为: (1)根据系统稳态误差的要求,确定系统的开环增益 K ; (2)在已确定 K 值的条件下,计算未校正系统的相位裕度; (3)根据指标的要求,确定在系统中 需要增加的相角超前量 ϕ m ; (4)由式( 6.3.2)确定 α 值,然后根据式( 6.3.3)确定最大 超前角对应的频率 ω m 处的对数幅频特性值 Lm , 即 j a a j lg jaT jT L lg m m m + + = + + = 1 1 1 20 1 1 20 ω ω 。 在未校正系统的对数幅频特性图 上找到幅值等于 点所对应的频率,该频率即为校正后系统新 的剪切频率 − Lm ωc ′,同时也是所选超前网络的 ω m,在此频率上超前网 络将产生最大超前相角值 ϕ m ;根据 ω m,确定 T 和 αT ; (5)确定超前校正环节的转折频率 T T 1 ω 1 = , ( T ) T α ω 1 2 = ; (6)验算。 3.相位超前校正的特点 (1)相位超前校正主要对未校正系统 在中频段的特性进行校 正。以确保校正后系统具有较高的 相位裕度及中频段斜率等于 − 20dB / dec 。 (2)超前校正可以提高系统响应的快 速性。相位超前校正环 节校正使系统截止频率增大,提高系统的响应速度。但随着带宽