
常见函数的Laplace变换 1(t) 2 t> 口3 e at 1 s+a 4 O Snot→ s2+02 5 S cos wt s2+ 2
常见函数的Laplace变换 1 2 3 4 5 s t 1 1( ) → 2 1 s t → s a e at + − → 1 2 2 sin + → s t 2 2 cos + → s s t

第二章控制系统的数学模型 口线性系统:系统的数学模型能用 线性微分方程描述。 口线性定常系统:微分方程的系数 为常数。 口线性系统满足叠加原理。 建立数学模型的方法:分析法和 实验法
线性系统:系统的数学模型能用 线性微分方程描述。 线性定常系统:微分方程的系数 为常数。 线性系统满足叠加原理。 建立数学模型的方法:分析法和 实验法。 第二章控制系统的数学模型

2.1控制系统的微分方程 一 列写微分方程的一般方法 列写系统(或元件)的微分方程,目 的在于确定系统的输出量与给定输入量或 扰动输入量之间的函数关系。 口确定系统(或元件)的输入量和输出量 口从系统输入端开始,列写各个环节的动态微分方程 口消除中间变量,得出输入输出之间关系的微分方程 整理得出微分方程
确定系统(或元件)的输入量和输出量 从系统输入端开始,列写各个环节的动态微分方程 消除中间变量,得出输入输出之间关系的微分方程 整理得出微分方程 2.1控制系统的微分方程 一 列写微分方程的一般方法 列写系统(或元件)的微分方程,目 的在于确定系统的输出量与给定输入量或 扰动输入量之间的函数关系
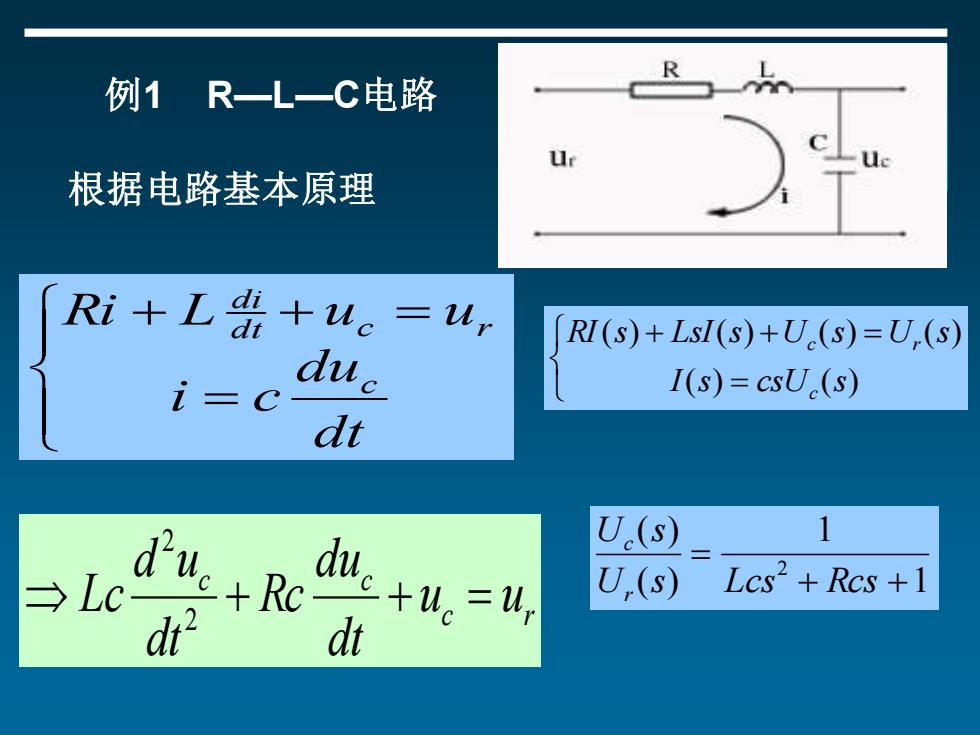
例1R一L一C电路 根据电路基本原理 Ri+Ldi+ue =ur RI(s)+LsI(s)+U(s)=U,(s) i=C due I(s)=csU(s) dt U.(s) 1 +R →Lc- du ur U(s) Lcs2+Rcs+1 r
例1 R—L—C电路 = + + = dt du i c Ri L u u c dt c r di c r c c u u dt du Rc dt d u Lc + + = 2 2 根据电路基本原理 = + + = ( ) ( ) ( ) ( ) ( ) ( ) I s csU s RI s LsI s U s U s c c r 1 1 ( ) ( ) 2 + + = U s Lcs Rcs U s r c
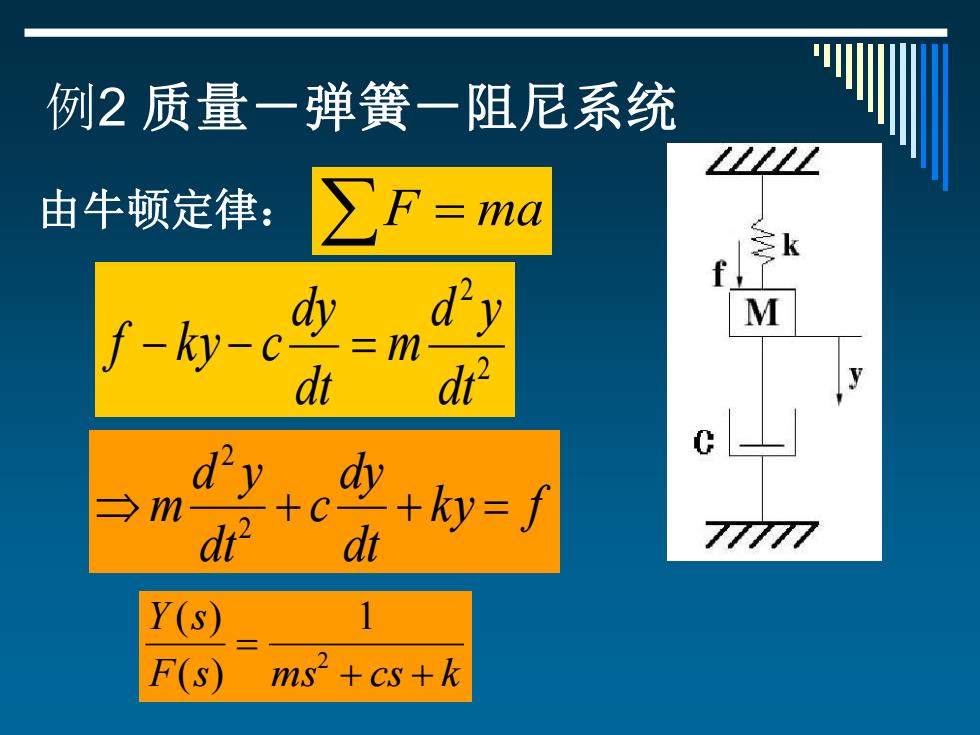
例2质量一弹簧一阻尼系统 由牛顿定律: ∑F=ma f-ky- dy二 d dt d m ay+c dr 内+y=∫ 77777 Y(s) F(s) ms+cs+k
例2 质量-弹簧-阻尼系统 由牛顿定律: F = ma 2 2 dt d y m dt dy f − k y − c = k y f dt dy c dt d y m + + = 2 2 F s ms cs k Y s + + = 2 1 ( ) ( )