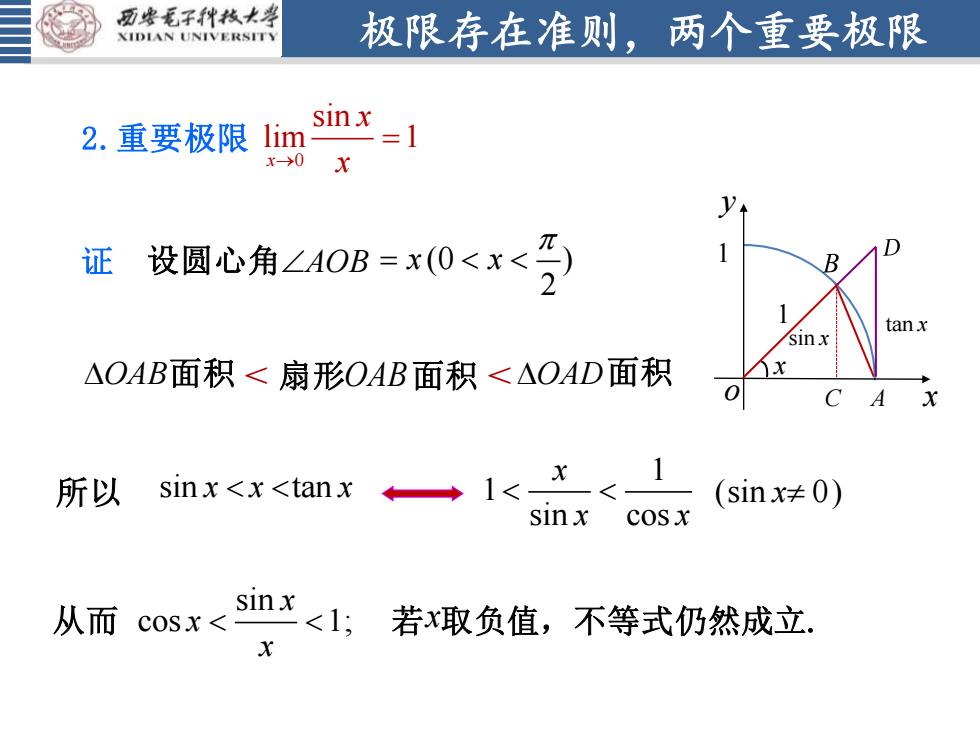
西安毛子科技大学极限存在准则,两个重要极限XIDIANUNIVERSITsinx12.重要极限limx->0xy证设圆心角ZAOB=x(O<x2tanxsinxxAOAB面积<扇形OAB面积<△OAD面积oC+A1x所以sinx<x <tanx(sin x± 0)sin xcos xsinx从而<1: 若x取负值,不等式仍然成立cosxx
极限存在准则,两个重要极限 证 2.重要极限 0 sin lim 1 x x → x = 设圆心角 AOB o C x y OAB 面积 扇形 OAB 面积 OAD 面积 1 1 1 sin tan 2 2 2 所以 x x x sin cos 1; x x x 从而 1 1 sin cos x x x (sin 0) x 1 A x 1 (0 ) 2 x x = 若 x 取负值,不等式仍然成立. sin tan x x x sin x tan x
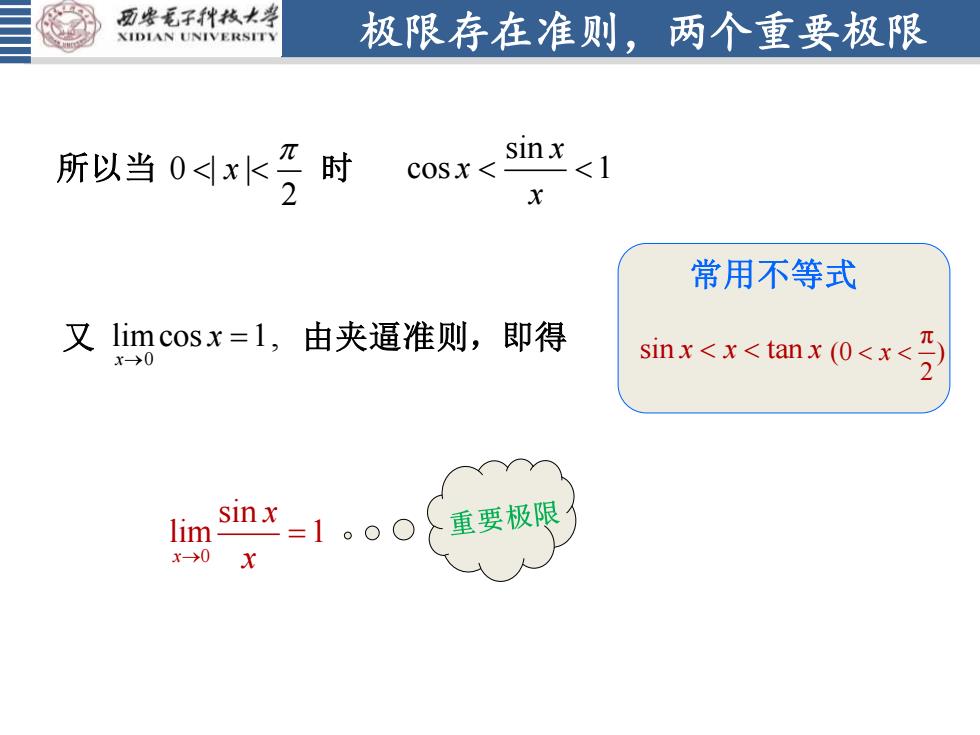
西安毛子科技大学极限存在准则,两个重要极限XIDIANUNIVERSITYsinx所以当0x时<1cosx <2x常用不等式又 limcosx=1,由夹逼准则,即得元sin x<x<tan x (0< x<x-→02sinx重要极限lim.00x->0x
极限存在准则,两个重要极限 由夹逼准则,即得 sin cos 1 x x x 0 sin lim 1 x x → x = 又 0 limcos 1, x x → = 常用不等式 sin tan x x x π (0 ) 2 x 所以当 0 | | 时 2 x
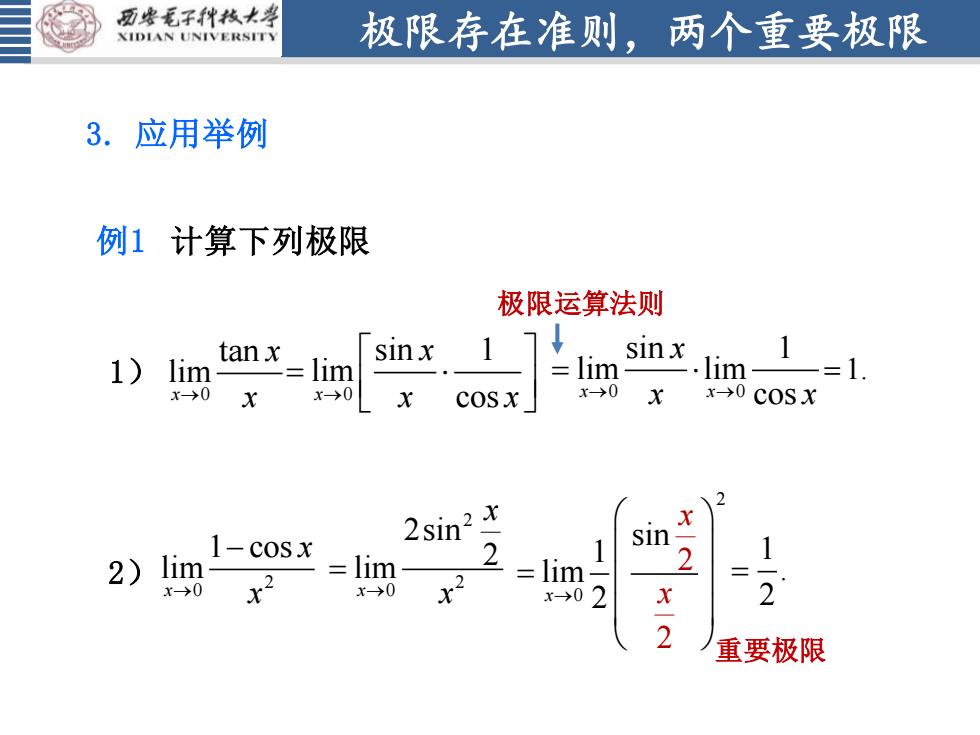
西安毛子科技大学极限存在准则,两个重要极限XIDIANUNIVERSITS3.应用举例例1计算下列极限极限运算法则sinx1一sinxtan x1)limlimlim1lim-x→0x->0x->0x-→>0xxcosxxcos x2sin2xxsin11-cos x212lim= lim2)=limR2x-→0x-→0x→0 2x2重要极限
极限存在准则,两个重要极限 3. 应用举例 例1 计算下列极限 1) =1. 2) 2 0 1 cos lim x x → x − 2 2 0 2sin 2 lim x x → x = 1 . 2 = 2 0 2 2 sin 1 limx 2 x → x = 0 tan lim x x → x 0 sin 1 lim cos x x → x x = 0 0 sin 1 lim lim cos x x x → → x x = 重要极限 极限运算法则