导 学以致用 1.如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E是 棱AB上的动点.若异面直线AD,与EC所成的角为60°,试确定 动点E的位置 A E B
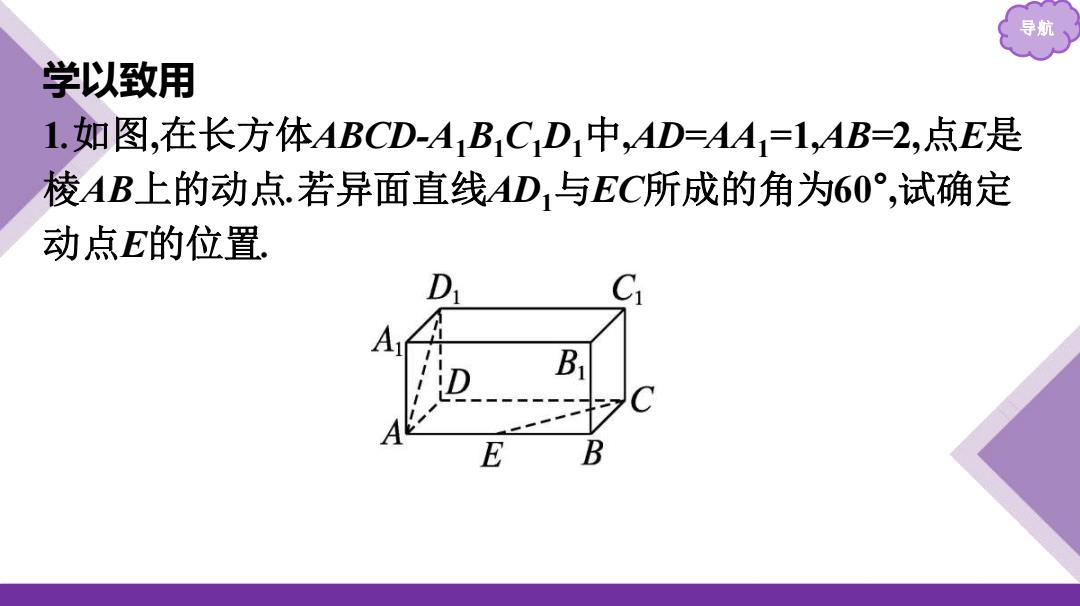
导航 学以致用 1.如图,在长方体ABCD-A1B1C1D1中,AD=AA1 =1,AB=2,点E是 棱AB上的动点.若异面直线AD1与EC所成的角为60° ,试确定 动点E的位置
解:以D为原点,DA,DC,DD,所在直线分别为x轴、y轴、轴, 建立空间直角坐标系,如图所示 则A(1,0,0),D10,0,1),C(0,2,0) 设E(1t,0)0≤≤2),则D1A=(1,0,-1), A CE=(1,t-2,0) 设异面直线AD1与EC所成的角为0, cos 0-lcOs<DA,CE14-CE 1 D AICE 1-2 V2-1+t-2)2 又0≤≤2,所以仁1.所以,点E为AB的中点
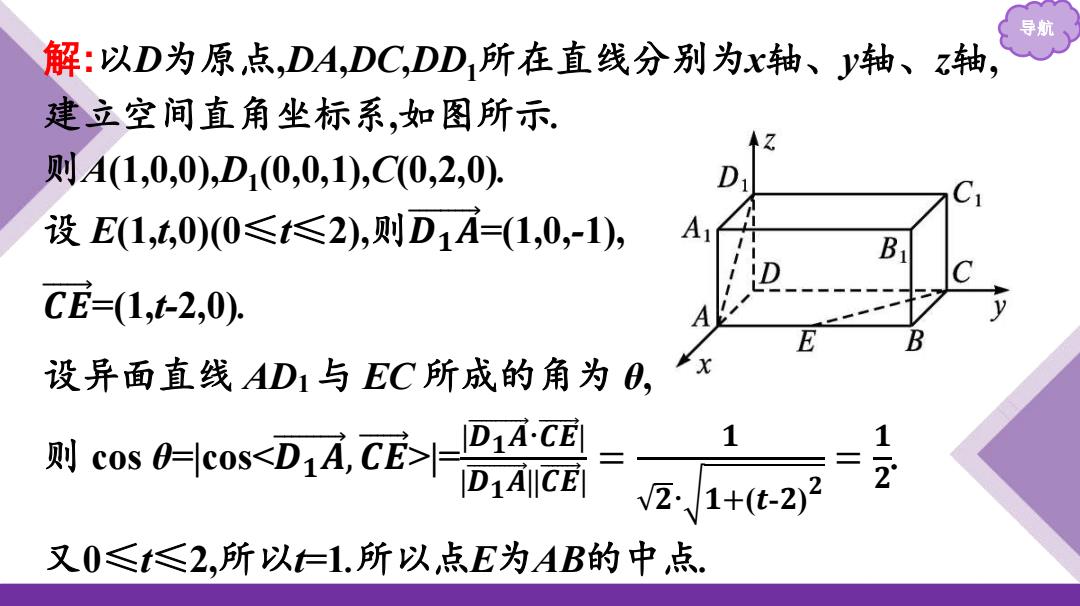
导航 解:以D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴, 建立空间直角坐标系,如图所示. 则A(1,0,0),D1 (0,0,1),C(0,2,0). 设 E(1,t,0)(0≤t≤2),则𝑫 𝟏 𝑨 =(1,0,-1), 𝑪 𝑬 =(1,t-2,0). 设异面直线 AD1与 EC 所成的角为 θ, 则 cos θ=|cos<𝑫 𝟏 𝑨 ,𝑪 𝑬 >|=|𝑫 𝟏 𝑨 ·𝑪 𝑬 | |𝑫 𝟏 𝑨 ||𝑪 𝑬 | = 𝟏 𝟐· 𝟏+(𝒕-𝟐) 𝟐 = 𝟏 𝟐 . 又0≤t≤2,所以t=1.所以点E为AB的中点

导期 二求直线与平面所成的角 典例剖析 2.已知正三棱柱ABC-A1BC1的底面边长为a,侧棱长为V2a,M 为AB,的中点,求BC,与平面AMC,所成角的正弦值 解:如图,以AB的中点O为原点,建立空 间直角坐标系, 则A(0,0),B(0,0),M00,V2a, C(0,,2a
导航 二 求直线与平面所成的角 典例剖析 2.已知正三棱柱ABC-A1B1C1的底面边长为a,侧棱长为 a,M 为A1B1的中点,求BC1与平面AMC1所成角的正弦值. 2 解:如图,以AB的中点O为原点,建立空 间直角坐标系, 则 A - 𝑎 2 ,0,0 ,B 𝑎 2 ,0,0 ,M(0,0, 2a), C1 0, 3𝑎 2 , 2a