
例 11 一个有两个孩子的家庭有四种情形(BB,GG,BG, GB),假设是等可能的。事件E是两个孩子的家 庭有两个男孩,事件F是两个孩子的家庭至少有 一个男孩。事件E和F是否独立? 解:p(E)=1/4,p(F=3/4,,p(E∩F)=1/4, p(E)p(F)=3/16≠1/4=pE∩F).E和F不是独立的
例 一个有两个孩子的家庭有四种情形 (BB, GG, BG, GB),假设是等可能的。事件E是两个孩子的家 庭有两个男孩,事件F是两个孩子的家庭至少有 一个男孩。事件E和F是否独立? 11

例:三门问题 12 蒙蒂.霍尔游戏(电视节目,Monty Hall Puzzle) 1 2 1/3(总是不变) 23(总是改变)
例:三门问题 12

例:三门问题 13 。 假设你正在参加一个有奖游戏。 ·你被要求在三扇门中选择一扇,其中一扇后面有一辆车, 其余两扇后面则是山羊; ·你选择了一道门; 。 然后知道门后面有什么的主持人,开启了另一扇后面有 山羊的门。 。 他然后问你:“你想改变主意而选择剩下来的这个门 吗?” ·问题是:改变选择对你来说有利吗?
例:三门问题 • 假设你正在参加一个有奖游戏。 • 你被要求在三扇门中选择一扇,其中一扇后面有一辆车, 其余两扇后面则是山羊; • 你选择了一道门; • 然后知道门后面有什么的主持人,开启了另一扇后面有 山羊的门。 • 他然后问你:“你想改变主意而选择剩下来的这个门 吗?” • 问题是:改变选择对你来说有利吗? 13
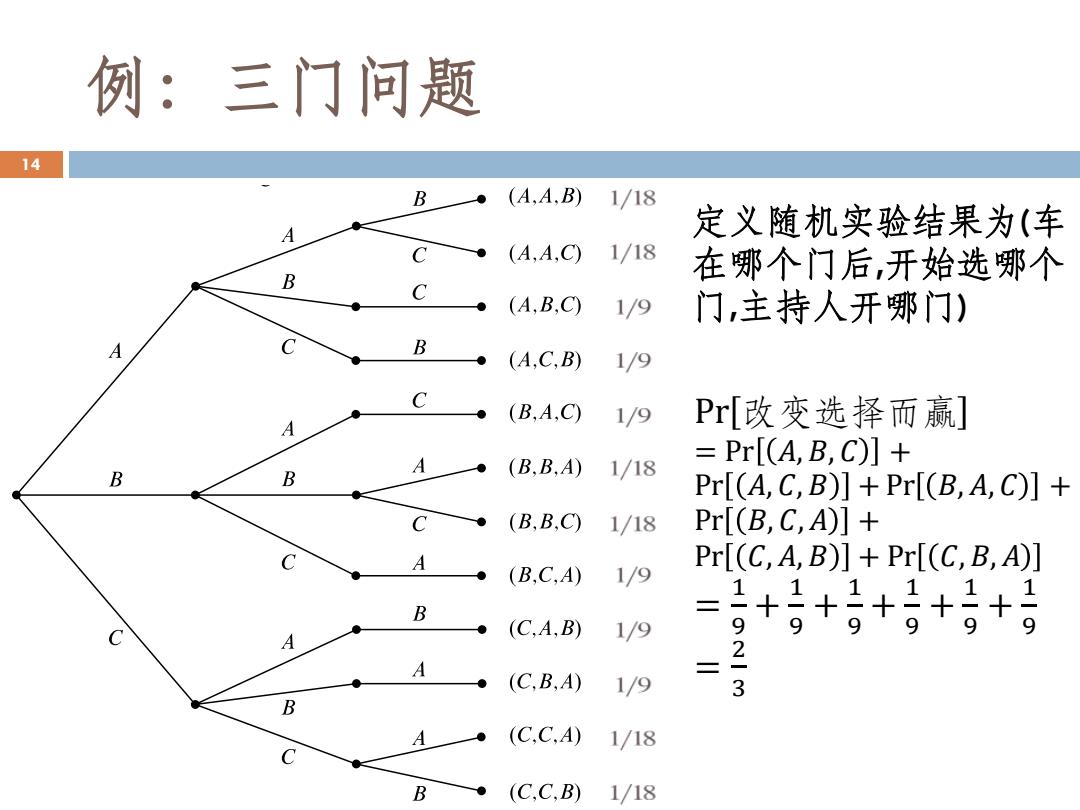
例:三门问题 14 B (A,A.B) 1/18 A 定义随机实验结果为(车 C (A,A,C) 1/18 在哪个门后,开始选哪个 B C (A,B,C) 1/9 门,主持人开哪门) C B (A,C,B) 1/9 C (B.A,C) 1/9 A Pr[改变选择而赢] = A Pr[(A,B,C)]+ B B (B,B,A) 1/18 Pr[(A,C,B)]+Pr[(B,A,C)]+ C (B.B.C) 1/18 Pr[(B,C,A)]+ C A Pr[(C,A,B)]+Pr[(C,B,A)] (B.C.A) 1/9 B C (C.A,B) 1/9 ++5+后++ 9 9 9 A A (C,B,A) 1/9 3 B A (C.C.A) 1/18 C B (C.C.B) 1/18
例:三门问题 14 定义随机实验结果为(车 在哪个门后,开始选哪个 门,主持人开哪门) Pr 改变选择而赢 = Pr 𝐴, 𝐵, 𝐶 + Pr 𝐴, 𝐶, 𝐵 + Pr 𝐵, 𝐴, 𝐶 + Pr 𝐵, 𝐶, 𝐴 + Pr 𝐶, 𝐴, 𝐵 + Pr 𝐶, 𝐵, 𝐴 = 1 9 + 1 9 + 1 9 + 1 9 + 1 9 + 1 9 = 2 3

本节提要 口内容1:概率论 口概率函数、条件概率、独立性 口内容2:贝叶斯定理 口内容3:随机变量及其期望与方差
内容1:概率论 概率函数、条件概率、独立性 内容2:贝叶斯定理 内容3:随机变量及其期望与方差 本节提要