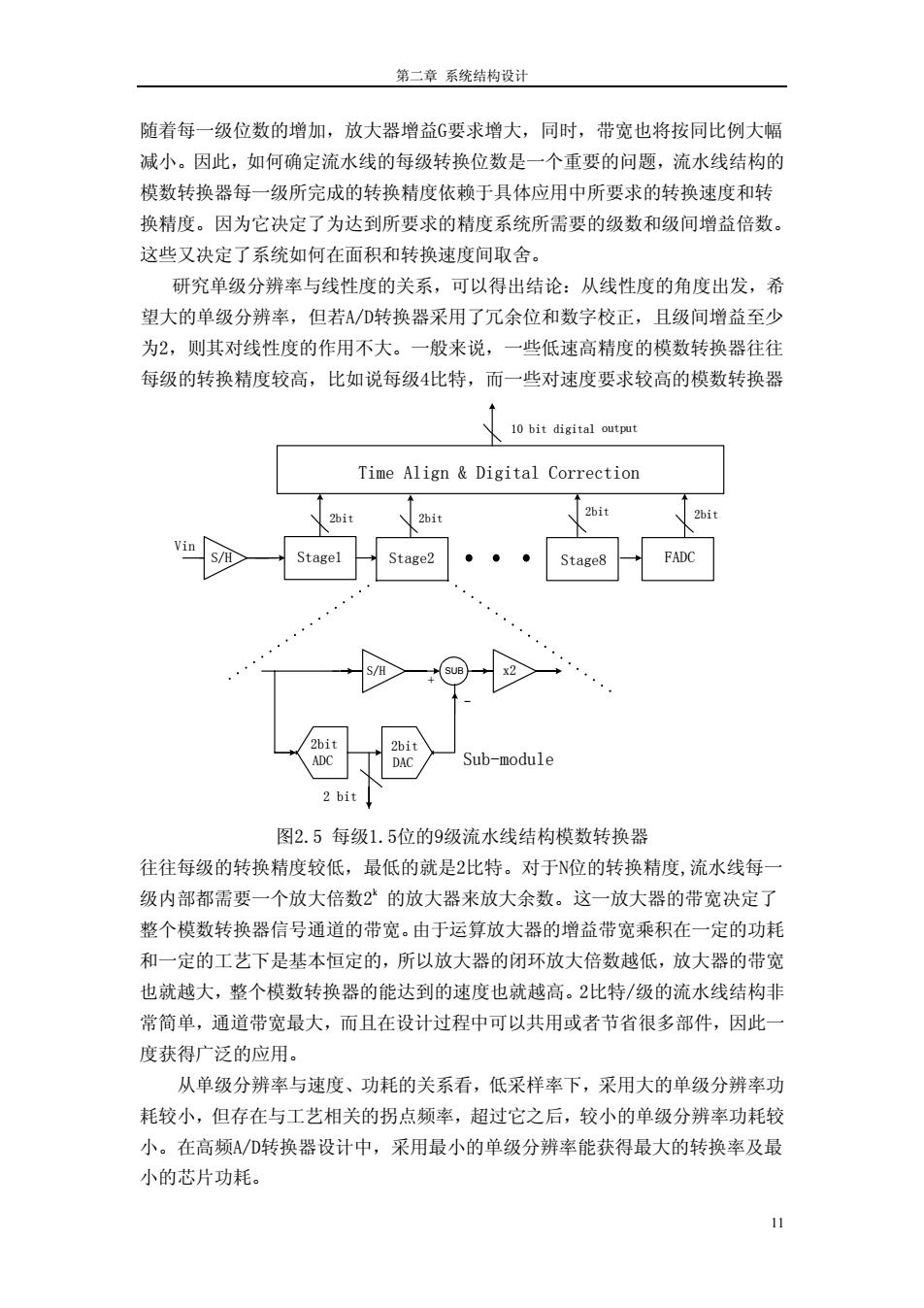
第二章系统结构设计 随着每一级位数的增加,放大器增益G要求增大,同时,带宽也将按同比例大幅 减小。因此,如何确定流水线的每级转换位数是一个重要的问题,流水线结构的 模数转换器每一级所完成的转换精度依赖于具体应用中所要求的转换速度和转 换精度。因为它决定了为达到所要求的精度系统所需要的级数和级间增益倍数。 这些又决定了系统如何在面积和转换速度间取舍。 研究单级分辨率与线性度的关系,可以得出结论:从线性度的角度出发,希 望大的单级分辨率,但若A/D转换器采用了冗余位和数字校正,且级间增益至少 为2,则其对线性度的作用不大。一般来说,一些低速高精度的模数转换器往往 每级的转换精度较高,比如说每级4比特,而一些对速度要求较高的模数转换器 10 bit digital output Time Align Digital Correction 2bit 2bit 2bit 2bit Stagel Stage2 Stage8 FADC /H 2bit 2bit ADC DAC Sub-module 2 bit 图2.5每级1.5位的9级流水线结构模数转换器 往往每级的转换精度较低,最低的就是2比特。对于位的转换精度,流水线每一 级内部都需要一个放大倍数2的放大器来放大余数。这一放大器的带宽决定了 整个模数转换器信号通道的带宽。由于运算放大器的增益带宽乘积在一定的功耗 和一定的工艺下是基本恒定的,所以放大器的闭环放大倍数越低,放大器的带宽 也就越大,整个模数转换器的能达到的速度也就越高。2比特/级的流水线结构非 常简单,通道带宽最大,而且在设计过程中可以共用或者节省很多部件,因此一 度获得广泛的应用。 从单级分辨率与速度、功耗的关系看,低采样率下,采用大的单级分辨率功 耗较小,但存在与工艺相关的拐点频率,超过它之后,较小的单级分辨率功耗较 小。在高频A/D转换器设计中,采用最小的单级分辨率能获得最大的转换率及最 小的芯片功耗。 11
第二章 系统结构设计 随着每一级位数的增加,放大器增益G要求增大,同时,带宽也将按同比例大幅 减小。因此,如何确定流水线的每级转换位数是一个重要的问题,流水线结构的 模数转换器每一级所完成的转换精度依赖于具体应用中所要求的转换速度和转 换精度。因为它决定了为达到所要求的精度系统所需要的级数和级间增益倍数。 这些又决定了系统如何在面积和转换速度间取舍。 研究单级分辨率与线性度的关系,可以得出结论:从线性度的角度出发,希 望大 往往每级的转换精度较低,最低的就是2比特。对于N位的转换精度,流水线每一 度、功耗的关系看,低采样率下,采用大的单级分辨率功 的单级分辨率,但若A/D转换器采用了冗余位和数字校正,且级间增益至少 为2,则其对线性度的作用不大。一般来说,一些低速高精度的模数转换器往往 每级的转换精度较高,比如说每级4比特,而一些对速度要求较高的模数转换器 Stage1 2bit 2bit 2bit Time Align & Digital Correction 10 bit digital output S/H SUB + - x2 2bit ADC 2bit DAC 2 bit S/H Vin Sub-module Stage2 2bit Stage8 FADC 图2.5 每级1.5位的9级流水线结构模数转换器 级内部都需要一个放大倍数2k 的放大器来放大余数。这一放大器的带宽决定了 整个模数转换器信号通道的带宽。由于运算放大器的增益带宽乘积在一定的功耗 和一定的工艺下是基本恒定的,所以放大器的闭环放大倍数越低,放大器的带宽 也就越大,整个模数转换器的能达到的速度也就越高。2比特/级的流水线结构非 常简单,通道带宽最大,而且在设计过程中可以共用或者节省很多部件,因此一 度获得广泛的应用。 从单级分辨率与速 耗较小,但存在与工艺相关的拐点频率,超过它之后,较小的单级分辨率功耗较 小。在高频A/D转换器设计中,采用最小的单级分辨率能获得最大的转换率及最 小的芯片功耗。 11

第二章系统结构设计 每级产生2位输出,其中1位作为冗余校正位,通常称之为每级1.5的流水线结 构,如图2.5所示。1.5比特/级的结构能够比较方便的校正电路中一些非理想因素 造成的误差,而且,由于它对比较器失调不敏感,使得电路可采用动态比较器来 减小静态功耗。每级的子模数转换器只需要两个比较器,每个比较器只需要两个 比较电平,并且在把数字电平转换成模拟量的过程中,只需要两个参考电平。它 极大的简化了MDAC电路的设计,同时级间增益为2也使得采样保持放大器在给定 功耗下可以获得最大的带宽。因此,在目前的高速流水线模数转换器设计中,每 级1.5比特是常见的结构。 本篇论文中采用的9级1.5比特/级的10位流水线结构模数转换器。模拟输入 在采样保持电路后由第一级内部的子模数转换器产生两位数字输出,同时作为第 二级余量增益电路(MDAC)的输入,与保持的输入信号相减,余量放大2倍。这 之后每级均量化两位输出,9级共产生18位的数字输出,最后一级是标准的两位 全并行结构,无需校正。18位的数字输出经过延时对齐后由数字校正电路通过冗 余信息消除比较器失调误差,并产生最终的10位量化输出。 图2.6是流水线模数转换器工作的时序分配示意图。流水线结构采用两相非 交叠时钟交替工作,相邻两级电路分别处于采样和保持两个不同的阶段,即奇数 级电路进行采样的时候,偶数级电路保持,偶数级电路进行采样的时候,奇数级 电路对数据进行保持。 Stage Stage n 2 bit Sample for even Hold for even numbered stage numbered stage clkl Sample for odd 中 clk2 numbered stage Hold for odd mumbered st边ge Digital calibrition 10 bit digital output 图2.6流水线的时序分配图 图2.7各级量化输出的同步 图2.7是流水线模数转换器的同步方案,由于采用两相时钟,相邻两级相差 半个时钟周期的延时,所以相邻两级产生的数字信号需要用不同时钟沿进行锁存 和对齐,也就是说第一级的输出延时半个时钟周期以后与第二级输出对齐,再 将这对齐后的4位输出延时半个时钟周期与第三级的输出对齐,这样经过四个时 钟周期的延时后,所有的18位数字输出可以对齐以进行数字校正。 2
第二章 系统结构设计 每级产生2位输出,其中1位作为冗余校正位,通常称之为每级1.5的流水线结 构,如 5比特/级的10位流水线结构模数转换器。模拟输入 在采 结构采用两相非 交叠 半个 图2.5所示。1.5比特/级的结构能够比较方便的校正电路中一些非理想因素 造成的误差,而且,由于它对比较器失调不敏感,使得电路可采用动态比较器来 减小静态功耗。每级的子模数转换器只需要两个比较器,每个比较器只需要两个 比较电平,并且在把数字电平转换成模拟量的过程中,只需要两个参考电平。它 极大的简化了MDAC电路的设计,同时级间增益为2也使得采样保持放大器在给定 功耗下可以获得最大的带宽。因此,在目前的高速流水线模数转换器设计中,每 级1.5比特是常见的结构。 本篇论文中采用的9级1. 样保持电路后由第一级内部的子模数转换器产生两位数字输出,同时作为第 二级余量增益电路(MDAC)的输入,与保持的输入信号相减,余量放大2倍。这 之后每级均量化两位输出,9级共产生18位的数字输出,最后一级是标准的两位 全并行结构,无需校正。18位的数字输出经过延时对齐后由数字校正电路通过冗 余信息消除比较器失调误差,并产生最终的10位量化输出。 图2.6是流水线模数转换器工作的时序分配示意图。流水线 时钟交替工作,相邻两级电路分别处于采样和保持两个不同的阶段,即奇数 级电路进行采样的时候,偶数级电路保持,偶数级电路进行采样的时候,奇数级 电路对数据进行保持。 Hold for even numbered stage Hold for odd numbered stage Sample for even numbered stage Sample for odd numbered stage clk1 clk2 Stage 1 Stage 2 Stage n Delay Delay Delay Delay Delay Digital calibrition 2 bit 2 bit 2 bit 10 bit digital output 图2.6 流水线的时序分配图 图2.7 各级量化输出的同步 图2.7是流水线模数转换器的同步方案,由于采用两相时钟,相邻两级相差 时钟周期的延时,所以相邻两级产生的数字信号需要用不同时钟沿进行锁存 和对齐 ,也就是说第一级的输出延时半个时钟周期以后与第二级输出对齐,再 将这对齐后的4位输出延时半个时钟周期与第三级的输出对齐,这样经过四个时 钟周期的延时后,所有的18位数字输出可以对齐以进行数字校正。 12

第二章系统结构设计 2.4每级1.5比特的流水线模数转换器算法 在流水线模数转换器的发展过程中,出现过许多的校正算法,其中最成功的 算法是l992年由Stephen H.Lewis提出的数字校正算法。这种算法的最大优点是 可以在很大程度上消除比较器的失调,而且很容易实现。因此,采用这种算法的 模数转换器具有达到更高分辨率的潜力。下面就以每级1.5位的流水线结构来介 绍这个算法。 每级1.5位算法的模数转换器中有两个比较器和两个判决电平,比较器的输 出通过编码逻辑电路后,得到的模数转换器输出为00、01、10三个编码。流水线 中前8级的转换曲线如图2.8所示,传输函数的关系如下: V≤V<V→d,01(二进制)台0(十进制) 4 V.(n)=2V 义≤V。<+e→d-0(=进o1K十进制 4 2V-Vrer +y.sV。<Vt→d=10(二进制)一2X十进制) 从传输函数关系和转换曲线图可以看出,只需要两个判决电平-0.5LSB、 0.5LSB,每一级的子模数转换器的转换范围都是4LSB(-2LSB~2LSB)。只要任 何一个判决电平的偏移距离不超过1/2LSB,都能够保证最终得出的余量增益被限 制在一2LSB~2LSB的范围以内,也就是没有超出下一级的转换范围,不会因为下 一级过载而引入非线性误差。这就意味着,只要子模数转换器的非线性误差小于 1/2LSB,该非线性误差都可以被后续的数字校正电路修正。 Residue Residue 00 01 10 ◆00 011011 2LSB 2LSB 1LSB 1LSB conv. conv. range range held Q held input input -1LSB -1LSB -2LSB -2LSB -1/4Vref 1/4Vret 图2.81.5位/级的流水线转换曲线 图2.92位/级的流水线转换曲线 6
第二章 系统结构设计 2.4 每级 1.5 比特的流水线模数转换器算法 在流水线模数转换器的发展过程中,出现过许多的校正算法,其中最成功的 算法是1992年由Stephen H.Lewis提出的数字校正算法。这种算法的最大优点是 可以在很大程度上消除比较器的失调,而且很容易实现。因此,采用这种算法的 模数转换器具有达到更高分辨率的潜力。下面就以每级1.5位的流水线结构来介 绍这个算法。 每级1.5位算法的模数转换器中有两个比较器和两个判决电平,比较器的输 出通过编码逻辑电路后,得到的模数转换器输出为00、01、10三个编码。流水线 中前8级的转换曲线如图2.8所示,传输函数的关系如下: i ref ref in ref 1 o i ref in ref 1 i ref ref in ref 1 1 2V +V -V V < - V d =01( 0 4 1 1 V (n)= 2V - V V <+ V d =01( 1 4 4 1 2V -V + V V <V d =10( 2 4 ⎧ ⎪ ≤ ⇒ ⇔ ⎪ ⎪ ⎨ ≤ ⇒ ⇔ ⎪ ⎪ ⎪ ≤ ⇒ ⇔ ⎩ 二进制) (十进制) 二进制) (十进制) 二进制) (十进制) 从传输函数关系和转换曲线图可以看出,只需要两个判决电平-0.5LSB、 0.5LSB,每一级的子模数转换器的转换范围都是4LSB (-2LSB~2LSB)。只要任 何一个判决电平的偏移距离不超过1/2LSB,都能够保证最终得出的余量增益被限 制在-2LSB~2LSB的范围以内,也就是没有超出下一级的转换范围,不会因为下 一级过载而引入非线性误差。这就意味着,只要子模数转换器的非线性误差小于 1/2LSB,该非线性误差都可以被后续的数字校正电路修正。 00 01 10 0 2LSB 1LSB -1LSB -2LSB Residue held input conv. range -1/4Vref 1/4Vref 00 01 10 0 2LSB 1LSB -1LSB -2LSB Residue held input conv. range 11 图2.8 1.5位/级的流水线转换曲线 图2.9 2位/级的流水线转换曲线 13

第二章系统结构设计 最后一级不可以校正,所以需要有三个标准的转换电平,仅为一个电压比较 型的2位ADC,转换曲线如图2.9所示,其量化输出函数如下: fV,>'/2 d=311)2 if0<V<'/2 d=2(10)2 if-'g/2<V<0 d=1(01)2 f V<-Vet 12 d=0(00)2 所谓数字校正电路就是根据流水线直接输出的数据位,纠正其中的子模数 转换器引入的非线性误差,从而得到最终的无冗余的数据位。考察直接相联系的 两级,分别称为当前级和下一级,假设下一级的两位数字信号已经被校正,校正 后的数据位分别称为b0c和a0c,而当前级的未校正的两位数据位分别称为bl和 al,那么可以根据简单的逻辑关系得出当前级校正后的数据位blc和alc。实际上 只要有b0c、bl、al就可以决定出blc和alc。也就是说,知道当前级的输出数据 和当前级的余数是大于零还是小于零,就可以唯一的确定出校正后的数据。比如 说当前级输出00,余数小于零,则校正后的数据仍然为00,如果余数大于零,则 校正后的数据为01。依此类推,可以得到完整的逻辑关系。 D H1 D LI D H,2 D L2 ● ● D H.8 D 1.8 D H9 DL.9 dio dg …d2ddo 图2.10数字校正算法 图2.10是数字误差校正算法的示意图,其中DH(n)、DL(n)分别表示第n 级数据输出的高位和低位。如果整个模数转换器的量程为[-Vref,Vref,那么这 种结构的最大优点在于它可以完全消除SUB-ADC中,比较器不大于Vref4的失调 误差。从图中可看出,这种算法的原理其实很简单,只需把每一级输出的量化值 错位相加即可得到最终的量化值。 g
第二章 系统结构设计 最后一级不可以校正,所以需要有三个标准的转换电平,仅为一个电压比较 型的2位ADC,转换曲线如图2.9所示,其量化输出函数如下: 2 2 2 / 2 3(11) 0 / 2 2(10) - / 2 0 1(01) / 2 i ref i ref ref i i ref if V V d if V V d if V V d f V V > = < < = < < = < − 2 d = 0(00) 所谓数字校正电路就是根据流水线直接输出的数据位,纠正其中的子模数 转换器引入的非线性误差,从而得到最终的无冗余的数据位。考察直接相联系的 两级,分别称为当前级和下一级,假设下一级的两位数字信号已经被校正,校正 后的数据位分别称为b0c和a0c,而当前级的未校正的两位数据位分别称为b1和 a1,那么可以根据简单的逻辑关系得出当前级校正后的数据位b1c和a1c。实际上 只要有b0c、b1、a1就可以决定出b1c和a1c。也就是说,知道当前级的输出数据 和当前级的余数是大于零还是小于零,就可以唯一的确定出校正后的数据。比如 说当前级输出00,余数小于零,则校正后的数据仍然为00,如果余数大于零,则 校正后的数据为01。依此类推,可以得到完整的逻辑关系。 D H,1 D L,1 D H,2 D L,2 D H,8 D l,8 + D H,9 D L,9 d10 d9 … d2 d1 d0 图2.10 数字校正算法 图2.10是数字误差校正算法的示意图,其中DH(n)、DL(n)分别表示第n 级数据输出的高位和低位。如果整个模数转换器的量程为[-Vref,Vref],那么这 种结构的最大优点在于它可以完全消除SUB-ADC中,比较器不大于Vref/4的失调 误差。从图中可看出,这种算法的原理其实很简单,只需把每一级输出的量化值 错位相加即可得到最终的量化值。 14
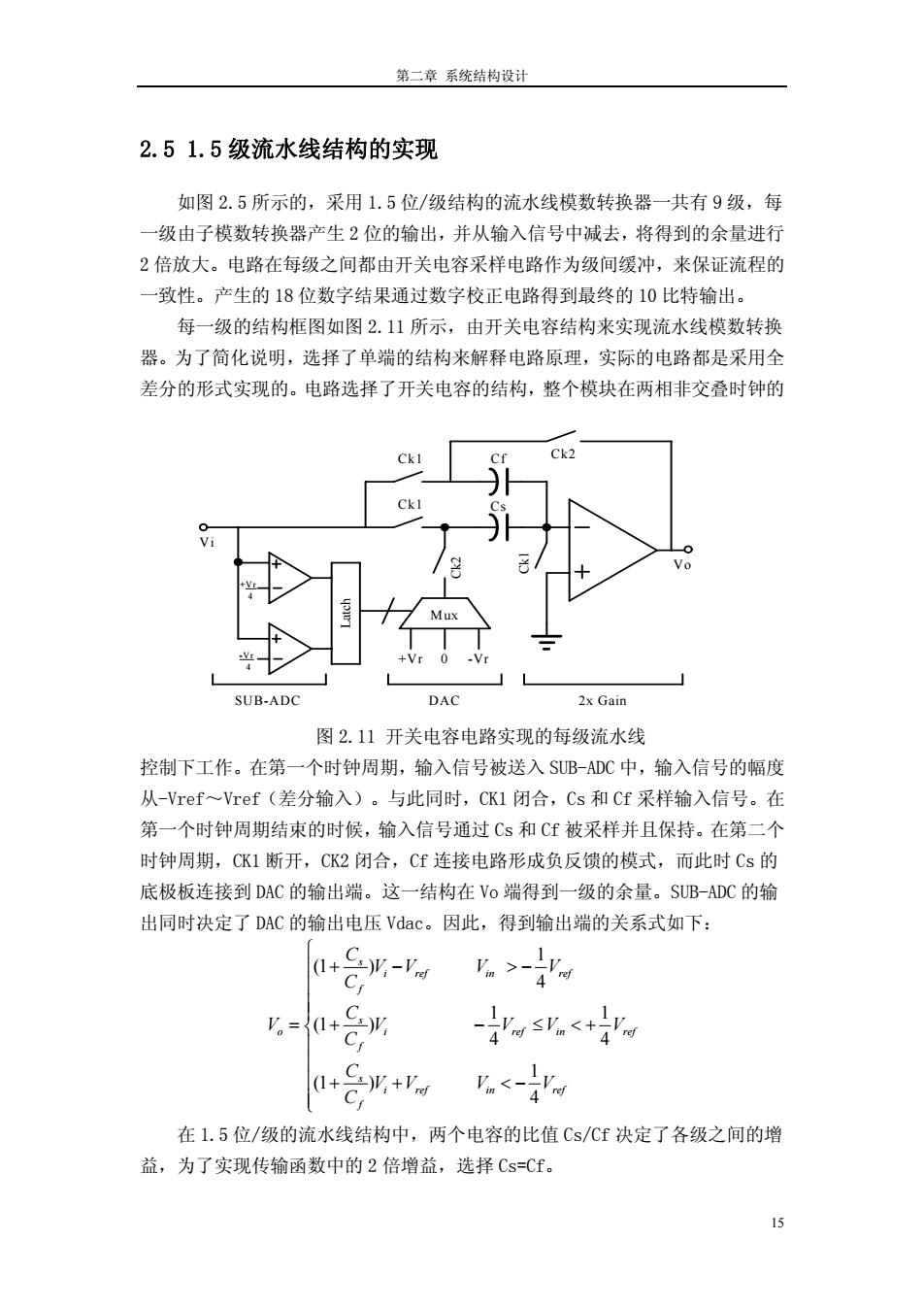
第二章系统结构设计 2.51.5级流水线结构的实现 如图2.5所示的,采用1.5位/级结构的流水线模数转换器一共有9级,每 级由子模数转换器产生2位的输出,并从输入信号中减去,将得到的余量进行 2倍放大。电路在每级之间都由开关电容采样电路作为级间缓冲,来保证流程的 一致性。产生的18位数字结果通过数字校正电路得到最终的10比特输出。 每一级的结构框图如图2.11所示,由开关电容结构来实现流水线模数转换 器。为了简化说明,选择了单端的结构来解释电路原理,实际的电路都是采用全 差分的形式实现的。电路选择了开关电容的结构,整个模块在两相非交叠时钟的 Ckl Ck2 ● SUB-ADC DAC 2x Gain 图2.11开关电容电路实现的每级流水线 控制下工作。在第一个时钟周期,输入信号被送入SUB-ADC中,输入信号的幅度 从-Vref~Vref(差分输入)。与此同时,CK1闭合,Cs和Cf采样输入信号。在 第一个时钟周期结束的时候,输入信号通过Cs和Cf被采样并且保持。在第二个 时钟周期,CK1断开,CK2闭合,Cf连接电路形成负反馈的模式,而此时Cs的 底极板连接到DAC的输出端。这一结构在Vo端得到一级的余量。SUB-ADC的输 出同时决定了DAC的输出电压Vdac。因此,得到输出端的关系式如下: (l+C-.-Vw F >-iV v=a+C g≤<+ 1 4'ref (1+ .V,+Vd m<- 4 ref 在1.5位/级的流水线结构中,两个电容的比值Cs/Cf决定了各级之间的增 益,为了实现传输函数中的2倍增益,选择Cs=Cf
第二章 系统结构设计 2.5 1.5 级流水线结构的实现 如图 2.5 所示的,采用 1.5 位/级结构的流水线模数转换器一共有 9 级,每 一级由子模数转换器产生 2 位的输出,并从输入信号中减去,将得到的余量进行 2 倍放大。电路在每级之间都由开关电容采样电路作为级间缓冲,来保证流程的 一致性。产生的 18 位数字结果通过数字校正电路得到最终的 10 比特输出。 每一级的结构框图如图 2.11 所示,由开关电容结构来实现流水线模数转换 器。为了简化说明,选择了单端的结构来解释电路原理,实际的电路都是采用全 差分的形式实现的。电路选择了开关电容的结构,整个模块在两相非交叠时钟的 +Vr 4 -Vr 4 +Vr 0 -Vr Mux Vi Latch Ck1 Ck1 Ck2 Ck1 Ck2 Cf Cs Vo SUB-ADC DAC 2x Gain 图 2.11 开关电容电路实现的每级流水线 控制下工作。在第一个时钟周期,输入信号被送入 SUB-ADC 中,输入信号的幅度 从-Vref~Vref(差分输入)。与此同时,CK1 闭合,Cs 和 Cf 采样输入信号。在 第一个时钟周期结束的时候,输入信号通过 Cs 和 Cf 被采样并且保持。在第二个 时钟周期,CK1 断开,CK2 闭合,Cf 连接电路形成负反馈的模式,而此时 Cs 的 底极板连接到 DAC 的输出端。这一结构在 Vo 端得到一级的余量。SUB-ADC 的输 在 1.5 位/级的流水线结构中,两个电容的比值 Cs/Cf 决定了各级之间 出同时决定了 DAC 的输出电压 Vdac。因此,得到输出端的关系式如下: 的增 益, 1 (1 ) 4 1 1 (1 ) 4 4 1 (1 ) 4 s i ref in ref f s o i ref in f s i ref in ref f C V V V V C C V V V V C C V V V V C ⎧ ⎪ + − > − ⎪ ⎪ ⎪ = + ⎨ − ≤ < + ⎪ ⎪ ⎪ + + < − ⎪⎩ Vref 为了实现传输函数中的 2 倍增益,选择 Cs=Cf。 15