
如何检验假设? 根据收集的资料,针对假设,给出检验方法,然后对 假设进行判断。 判断方法有二种:临界值法。P值法. 以例1为例来说明减肥药有效? 还是无效? 11
如何检验假设? 根据收集的资料,针对假设,给出检验方法,然后对 假设进行判断。 判断方法有二种:临界值法. P_值法. 以例1为例来说明减肥药有效? 还是无效? 11

设服用减肥药前后体重差值X~N(山,o), 并假定方差σ2=0.36. 检验假设:H。:u=0,H1:4>0, 注意到:是的无偏估计,的取值大小反映了的取值 大小,当原假设成立时,取值应偏小。因此 当灭≥C时,拒绝原假设H, 当灭<C时,接受原假设H, 其中C是待定的常数. 12
12 2 2 ~ ( 0.36. X N = 设服用减肥药前后体重差值 , ), 并假定方差 0 1 检验假设:H H : 0, : 0, = X X X 注意到: 是 的无偏估计, 的取值大小反映了 的取值 大小,当原假设成立时, 取值应偏小。因此 0 0 X C H X C H C 当 时,拒绝原假设 , 当 时,接受原假设 , 其中 是待定的常数

如果统计量T=T(X,,X,)的取值大小和原假设H。 是否成立有密切联系,可将其称为对应假设问题的 检验统计量,而对应于拒绝原假设H,时,样本值的 范围称为拒绝域,记为W,其补集币称为接受域 第二步:给出检验统计量,并确定拒 绝域的形式 原假设 本例中的检验统计量为灭,拒绝域为 W={(X,…,Xn):X≥C C如何选择?一关键问题
原假设 1 0 0 ( , . T T X X H n H W W 如果统计量 = , , )的取值大小和原假设 是否成立有密切联系,可将其称为对应假设问题的 ,而对应于拒绝原假设 时,样本值的 范围 检 称为 ,记为 其 验统 补集 称为 计量 拒绝域 接受域 1 , ( , , ) : n X W X X X C = 本例中的检验统计量为 拒绝域为 第二步:给出检验统计量,并确定拒 绝域的形式. 13 C如何选择?——关键问题

由于样本的随机性,任一检验规则在应用时,都有 可能发生错误的判断 两类错误。 原假设为真 原假设不真 根据样本拒绝原假设 第|类错误 正确 根据样本接受原假设正确 第川类错误 第类错误:拒绝真实的原假设(弃真). 第丨类错误:接受错误的原假设(取伪)
第I类错误:拒绝真实的原假设(弃真). 第II类错误:接受错误的原假设(取伪). 原假设为真 原假设不真 根据样本拒绝原假设 第I类错误 正确 根据样本接受原假设 正确 第II类错误 14 由于样本的随机性,任一检验规则在应用时,都有 可能发生错误的判断——两类错误
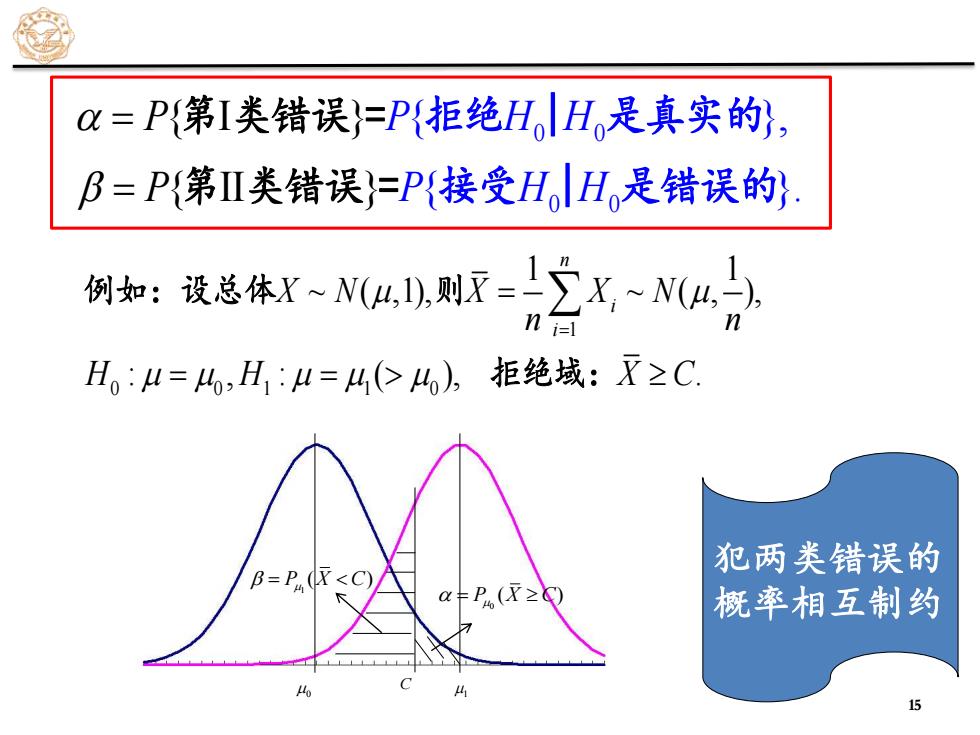
=P{第I类错误=P{拒绝HH是真实的, B=P{第Ⅱ类错误=P接受HH,是错误的 匆如:设总体r-NMu则7=∑X~N》 n i= H:4=4,H1:μ=4(C4o),拒绝域:X≥C 犯两类错误的 =P4 (≥& 概率相互制约
犯两类错误的 概率相互制约 0 0 0 0 { }, { { I } { II } }. P H H P H H P P = = 拒绝 | 是真实的 接 第 类错误 = 第 类错误 = 受 | 是错误的 1 0 0 1 1 0 1 1 ~ ( ,1), ~ ( , ), : , : ( ), . n i i X N X X N n n H H X C = = = = 例如:设总体 则 拒绝域: 0 1 C 0 P X C ( ) = 1 P X C ( ) = 15