
Neyman--Pear son,原则: 首先控制犯第I类错误的概率不超过某个常数 a∈(0,1),再寻找检验,使得犯第IⅡ类错误的 概率尽可能小.称为显著水平. 常取=0.01,0.05,0.1等. 16
0 I ,1 II 首先控制犯第 类错误的概率不超过某个常数 ( ),再寻找检验,使得犯第 类错误的 概 N 率 eyman-Pearson 尽可能小. 称 原则: 为显著水平. 常取 = 0.01 0.05 0.1 , , 等. 16

第三步,根据显著水平和统计量的分布确定临界 值—临界值法 在例1中,取显著水平0=0.05, 当H:=0成立时,、 ~N(0,1),统计量的分布) 619 犯第I类错误的概率可如下计算: r>ca=n=P5a6a- 105.5- 0.6/V9 ≥20.05=1.645.→C≥0.329 17
在例1中,取显著水平 = 0.05, 0 : 0 , ~ (0,1),( ) 0.6 / 9 X 当H N = 成立时 统计量的分布 犯第I类错误的概率可如下计算: 1 0.05. / C n = − = 0.05 1.645. 0.329. 0.6 / 9 C = z C { 0} 0 / / X C P X C P n n = = = 第三步,根据显著水平和统计量的分布确定临界 值——临界值法 (0.05 = −( z0.05 )) 17

根据Neyman-Pearson原则,为使犯第Ⅱ类错误的概率 尽可能小,应取C=0.329.因此,拒绝域W={X≥0.329} 第四步:根据样本得出结论. 根据实际样本资料,得x=0.522>0.329 当原假设H成立时,样本落在拒绝域的概率不超过 0.05,是小概率事件。 根据实际推断原理,有充分的理由拒绝原假设,认为 厂家的宣传是可靠的. 同理,若0=0.01,拒绝域W={X≥0.465,拒绝原假设
0.329 { 0.329}. N II . eyman Pearson C W X − = = 根据 原则,为使犯第 类错误的概率 尽可能小,应取 因此,拒绝域 根据实际样本资料,得x = 0.522 0.329. 当原假设H0成立时,样本落在拒绝域的概率不超过 0.05,是小概率事件。 根据实际推断原理,有充分的理由拒绝原假设,认为 厂家的宣传是可靠的. 第四步:根据样本得出结论. 18 同理,若 = = 0.01, { 0.465} 拒绝域W X ,拒绝原假设
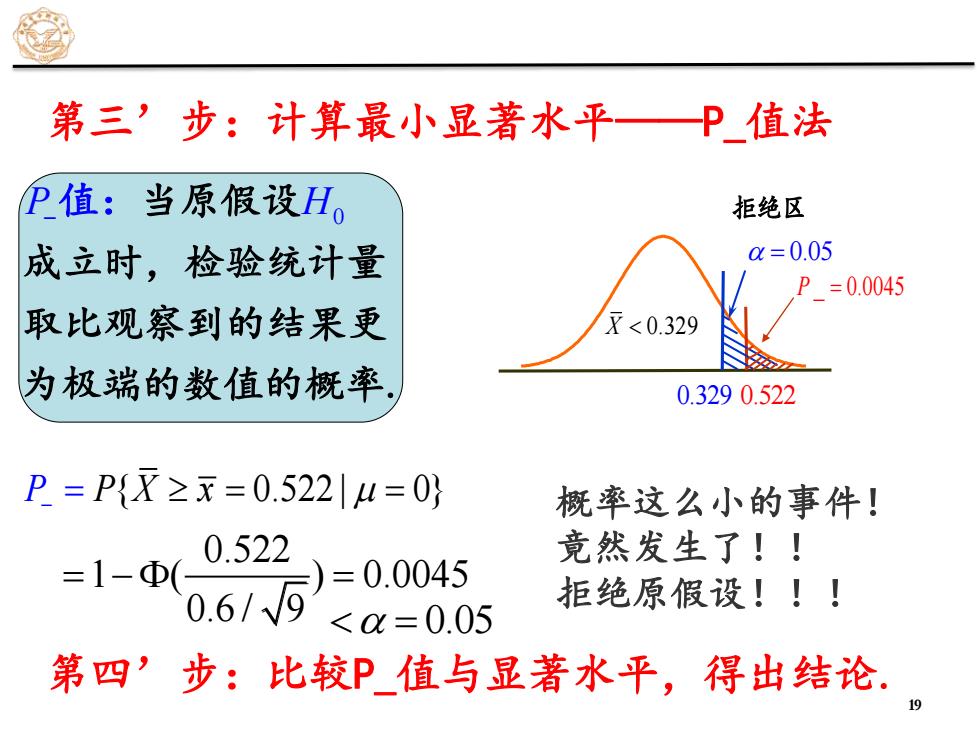
第三’步:计算最小显著水平—P值法 P值:当原假设H, 拒绝区 成立时,检验统计量 =0.05 P=0.0045 取比观察到的结果更 灭<0.329 为极端的数值的概率 0.3290.522 P=P{X≥x=0.522|u=0} 概率这么小的事件! 0.522 竟然发生了!」 =1-Φ( )=0.0045 .619 拒绝原假设!!」 <0=0.05 第四’步:比较P值与显著水平,得出结论
P H − 当原假设 0 成立时,检验统计量 取比观察到的结果更 为极端的数 值: 值的概率. P− = P X x { 0.522 | 0} = = 概率这么小的事件! 竟然发生了!! 拒绝原假设!!! 0.522 1 ( ) 0.0045 0.6 / 9 = − = 第三’步:计算最小显著水平——P_值法 第四’步:比较P_值与显著水平,得出结论. = 0.05 P _ 0.0045 = X 0.329 拒绝区 = 0.05 0.329 0.522 19

P值与显著水平o的关系: (1)若P≤心,等价于样本落在拒绝域内,因此,拒 绝原假设,称检验结果在水平α下是统计显著的. (2)若P>0,等价于样本不落在拒绝域内,因此, 不拒绝(接受)原假设,称检验结果在水平下 是统计不显著. 20
P P − (1)若 − ,等价于样本落在拒绝域内,因此,拒 绝原假设,称检验结果在水平 值与显著水平 : 统计 的 下是 关系 显著的. P (2)若 − ,等价于样本不落在拒绝域内,因此, 不拒绝(接受)原假设,称检验结果 统计 在水平 下 是 不显著. 20