
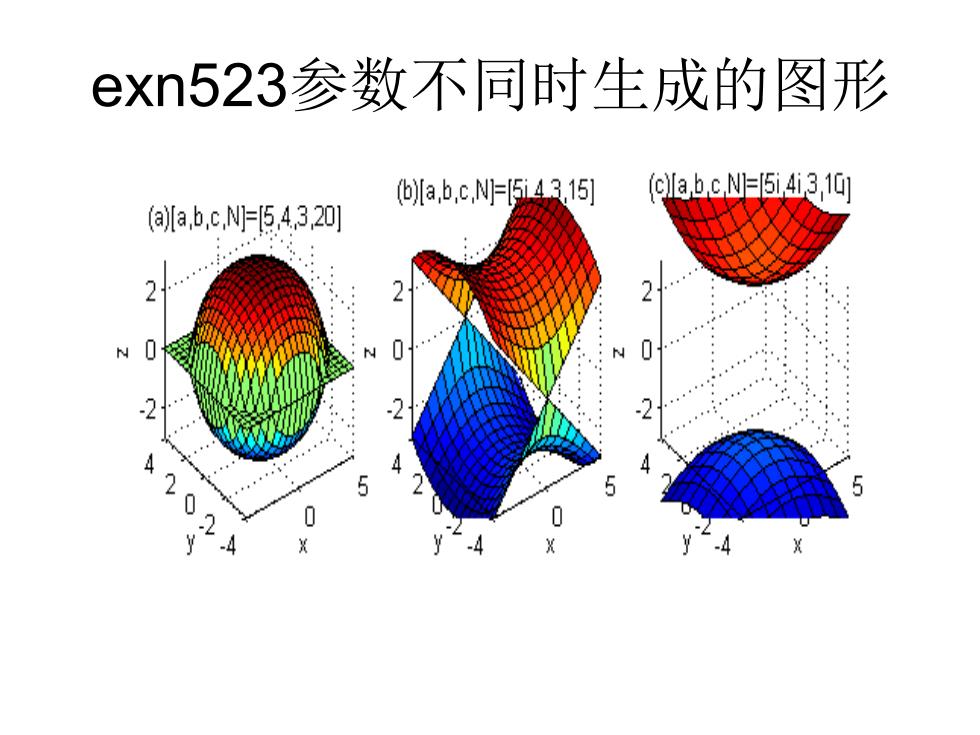
二.二次曲面的画法 ·【例5-2-3】二次曲面的方程如下 x2,y2, 2 要求讨论参数a,b,c对其形状的影响,并画出其图形。 ·解:◆原理数学模型很清楚,关键在于如何作出三维曲 面图形。首先是自变量x和y不再是一维数组,而要设置成 二维的矩阵(网格)。其次从上题中知道,在按给定xy求z 时有开方运算,有正有负,都要考虑在内: z=±c√1-x2/a2-y21b2 按此式计算,一是有正负两个解,这在上例中已经谈到: 二是在xy取某些值时,z会出现虚数。为了使虚数不出现 在surf中,把z的实部z1=real(z)作为三维绘图的因变量
二.二次曲面的画法 • 【例5-2-3】 二次曲面的方程如下 要求讨论参数a,b,c对其形状的影响,并画出其图形。 • 解:◆原理 数学模型很清楚,关键在于如何作出三维曲 面图形。首先是自变量x和y不再是一维数组,而要设置成 二维的矩阵(网格)。其次从上题中知道,在按给定x,y求z 时有开方运算,有正有负,都要考虑在内: • 按此式计算,一是有正负两个解,这在上例中已经谈到; 二是在x,y取某些值时,z会出现虚数。为了使虚数不出现 在surf中,把z的实部z1=real(z)作为三维绘图的因变量。 2 2 2 2 2 2 1 x y z a b c + + =2 2 2 2 z c x a y b = − − 1 / /

画圆锥曲面的程序exn523 %a,b为实数时得椭球,a为虚数时得鞍面,a,b为虚数时得双曲面, a=input('a=);b=input('b='); %输入参数a,b,c, c=input('c=);N=input('N=); %N为网格线的数目 grid=linspace(-abs(a),abs(a),N);%建立x网格坐标 ygrid=linspace(-abs(b),abs(b),N);%建立y网格坐标 [x,y]=meshgrid(xgrid,ygrid); %自变量xy矩阵 z=c*sqrt(1-y.*y/b/b-x.*x/a/a); %因变量矩阵 z1=real(z); %取z的实部z1(去掉虚数) surf(x,y,z1),hold on %画正负两半空间曲面 surf(x,y,-z1);
画圆锥曲面的程序exn523 % a,b为实数时得椭球,a为虚数时得鞍面,a,b为虚数时得双曲面, a=input('a=');b=input('b='); % 输入参数a,b,c, c=input('c=');N=input('N='); % N为网格线的数目 xgrid= linspace(-abs(a),abs(a),N); % 建立x网格坐标 ygrid= linspace(-abs(b),abs(b),N); % 建立y网格坐标 [x,y]=meshgrid(xgrid,ygrid); % 自变量x,y矩阵 z=c*sqrt(1-y.*y/b/b-x.*x/a/a); % 因变量矩阵 z1=real(z); % 取z的实部z1(去掉虚数) surf(x,y,z1),hold on % 画正负两半空间曲面 surf(x,y,-z1);
exn523参数不同时生成的图形 ba,b,cN=5i4315] (c)a,b.c.N]=5i4i3,10 aa,bc,F5.43,20] 4 0
exn523参数不同时生成的图形

用参数方程生成的椭球 ·【例5-2-4】与上述等价的椭球参数方程为: x=acosusinv, y=bsinusinv, Z=CCOSV 其中u的取值范围为02π,其几何意义是球面上 任何点向径的投影在xy平面上的方位角,即相当 于上例中的。V的取值范围是-π~+π,其几何意 义是球面上任何点向径的俯仰角。这个参数方程 避开了上下两半个椭球不同方程的衔接问题,使 它成为连续平滑过渡的同一个方程,既简化了程 序,画出的图形也漂亮得多
用参数方程生成的椭球 • 【例5-2-4】 与上述等价的椭球参数方程为: • 其中u的取值范围为0~2π,其几何意义是球面上 任何点向径的投影在xy平面上的方位角,即相当 于上例中的θ。v的取值范围是-π~+π,其几何意 义是球面上任何点向径的俯仰角。这个参数方程 避开了上下两半个椭球不同方程的衔接问题,使 它成为连续平滑过渡的同一个方程,既简化了程 序,画出的图形也漂亮得多。 cos sin , sin sin , cos x a u v y b u v z c v = = =