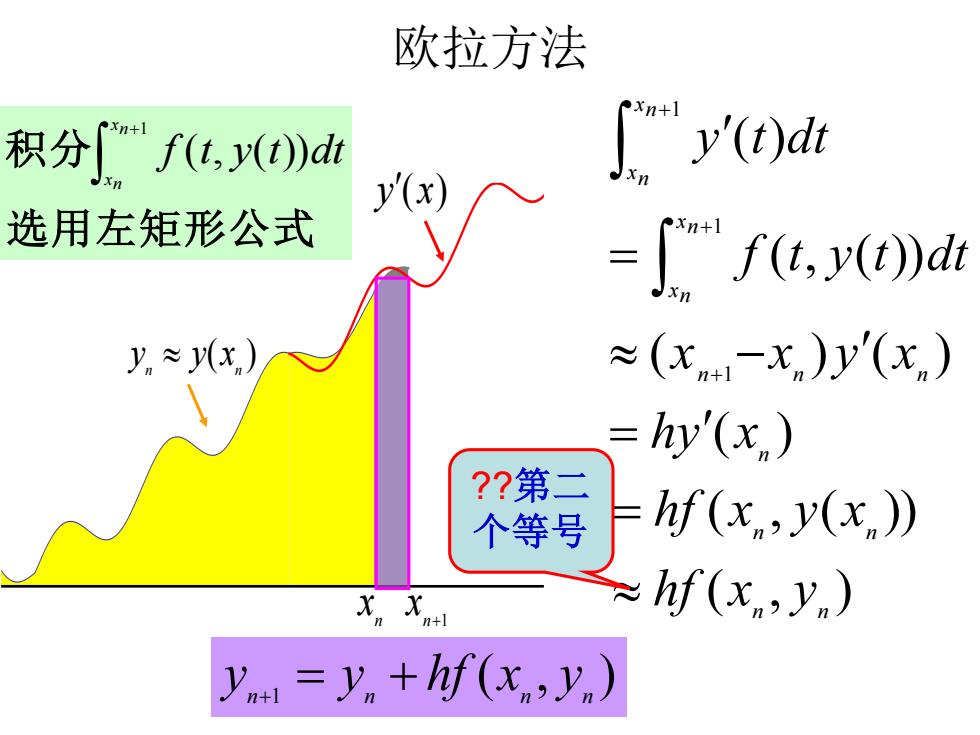
欧拉方法 xn+] 积分f(t,()》d y'(x) 选用左矩形公式 [""f(t,y(t)dt yn≈xn) ≈(xn1-xn)y'(xn) =hy'(x) ??第二 个等号 hf(x,y(x.)) XX hf(x.,y.) y=y.+hf(x,y)
欧拉方法 ( ) n n y y x y(x) n x n+1 x 选用左矩形公式 积分 +1 ( , ( )) x n x n f t y t dt ( ) ( ) ( ) ( , ( )) ( ) 1 1 1 n n n n x n x n x n x n hy x x x y x f t y t dt y t dt = − = + + + ( , ) ( , ( )) n n n n hf x y hf x y x = ??第二 个等号 ( , ) n 1 n n n y = y + hf x y +

y(x)=y(x,)+hf(x2y) 欧拉方法截断误差分析 假设(x)=y. y(x)=y(x,)+hy'(x)+O(h) =y(x,)+hf(x y(x,))+O(h) =y,+hf(x,y)+O(h) y=y.+hf(xy) y(x)-y1=O(h2) 精度较差
欧拉方法截断误差分析 ( ) ( ) ( , ) n 1 n n n y x = y x + hf x y + n n 假设y(x ) = y ( , ) ( ) ( ) ( , ( )) ( ) ( ) ( ) ( ) ( ) 2 2 2 1 y hf x y O h y x hf x y x O h y x y x hy x O h n n n n n n n n n = + + = + + + = + + ( , ) n 1 n n n y = y + hf x y + ( ) ( ) 2 y x n+1 − yn+1 = O h 精度较差
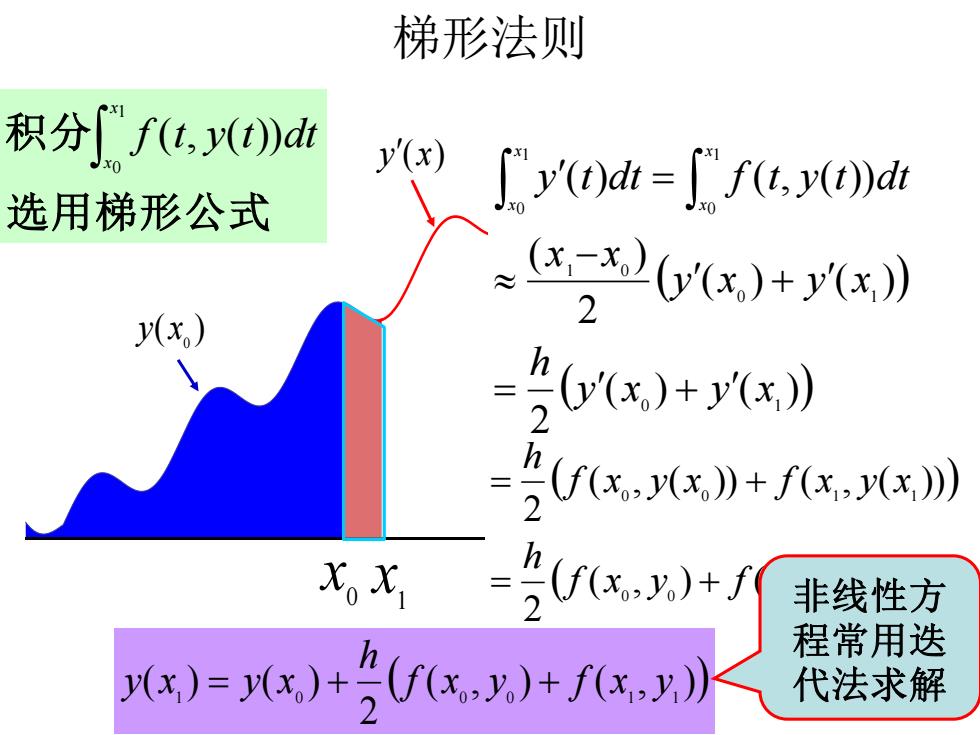
梯形法则 积分f(,y()d y(x) 选用梯形公式 y(Od=[f(t,y()dr 6yx,)+y'x)》 2 y(x.) hyx,)+(x》 ((x,x》+fx,(x川 )(f(x,y)+f 非线性方 )=x)+,)+fx,》 程常用迭 代法求解
( ) 0 y x y(x) 0 x 1 x 梯形法则 ( ) ( ( , ) ( , )) 2 ( , ( )) ( , ( )) 2 0 0 1 1 0 0 1 1 f x y f x y h f x y x f x y x h = + = + 选用梯形公式 积分 1 0 ( , ( )) x x f t y t dt ( ) ( ( ) ( )) 2 ( ) ( ) 2 ( ) ( ) ( , ( )) 0 1 0 1 1 0 1 0 1 0 y x y x h y x y x x x y t dt f t y t dt x x x x = + + − = ( ( , ) ( , )) 2 ( ) ( ) 1 0 0 0 1 1 f x y f x y h y x = y x + + 非线性方 程常用迭 代法求解